原文链接：https://aclanthology.org/2022.acl-long.490.pdf

ACL 2022

介绍

问题

        作者认为在命名实体任务中，由于实体的边界标注存在模糊、不一致的情况，比如一些实体中的冠词和修饰词。如下图所示中蓝色框和红色框中的内容都可以被认为是同一个实体，而目前基于span的NER模型，对于边界不正确的预测都认为是完全错误的，但是对于部分实体来说边界的区分并不是很明显，而这种硬标签性的评判就会导致模型受到干扰。

idea 

         因此作者受图像分类任务中标签平滑（比如标签（0，1）准换为： [0, 1] * (1 - 0.1) + 0.1/2 = [0.05, 0.95]）的启发，提出了boundary smooth，用于span-based的NER模型的正则化技术，将实体概率从标记的span重新按曼哈顿距离平均分配到其周围的span。

方法 

        作者所提出的只是一个减少过拟合的方法，由于主要改动是在decoder部分，因此对使用的Biaffine decoder进行了介绍，再介绍提出的boundary smoothing的应用。

Biaffine Decoder 

        对输入序列encode得到序列表征：，T表示序列的长度。

        decoder部分使用Biaffine作为baseline，两个前馈网络分别对x进行拟合，生成两个表征:和，分别对应于span的起点和终点。

        对于c个实体类别，给定一个span（i-j），使用以下公式计算出分数向量并送入一个分类器，得到这个sapn预测的分数 

        其中wj-i表示可学习矩阵中（j-i）宽度的embedding，U、W、b都是可学习参数。 

        ground-truth类别使用one-hot进行编码，该模型的交叉熵损失函数如下所示：

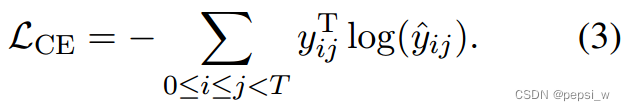
        在推理阶段，首先回对被预测为“non-entity”标签的span进行丢弃，然后按预测的分数进行排序，如果存在边界冲突的span，则会丢弃掉分数较低的span。 

Boundary Smoothing

        作者对句子中标注了两个实体的例子进行了可视化来解释boundary smooth，如下图所示。在之前的NER模型中，被标注的span肯定是一个实体，其他区域都不可能是实体，作者将这种称为hard boundary。但实体的边界是比较模糊的，因此作者将标记span周围的token也分配一定的可能性（），原标记span的分数为（1-）如b部分所示。

         

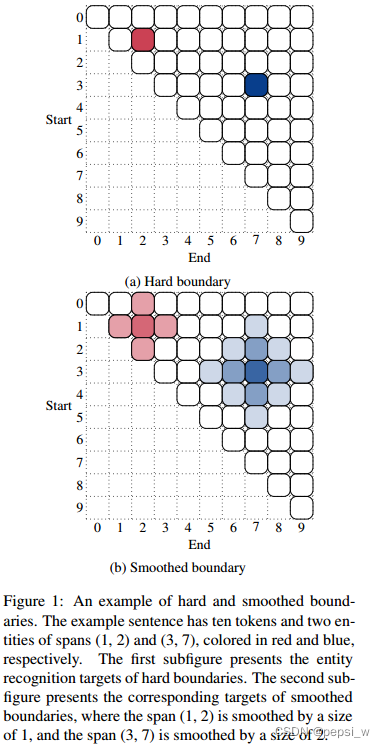
        主要是对原来标记的span周围的span分配一些分数，在平滑度为D时，所有与被标记实体的曼哈顿距离在d（d<D）以内的span都平分概率。这样进行调整后还可能性为0的span 分配“non-entity”标签。因此biaffine模型的损失函数修改为以下形式：

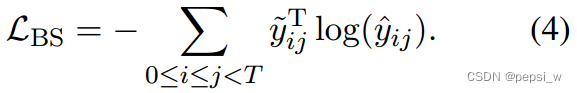
         其中为平滑处理后的分数。

         在数据集中，正样本被离散的分配到这些候选span上，原始数据集中一共有378万的候选span，但是仅有3.5w的实体，也就是说正样本只有0.93%，通过标签平滑将可能性分配给标注实体周围的span，也可以缓解原始数据集中正负样本不平衡的问题。

实验

对比实验

         在英文数据集上进行实验，结果如下所示：

         在中文数据集上的实验结果如下所示：

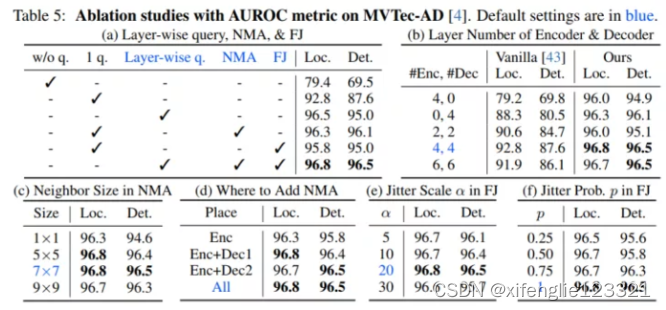
消融实验

         作者对边界平滑的参数和D的取值，以及使用标签平滑来代替边界平滑这两个内容进行了实验，结果如下所示：

         作者提到该超参数的设计与数据集有关，在新的数据集上进行实验则需要对参数进行微调。

        另外，作者认为标签之前是没有相关性的，因此使用标签平滑不仅不能提升模型的性能，甚至还会降低模型的消息（但是实验部分没有表现出来）。

        作者对模型的结构进行了消融实验，即在多个baseline上对所提出的边界平滑进行了实验，以证明该方法的鲁棒性。作者还将Robert与biaffine之间的BiLSTM进行了实验，结果表示去掉BiLSTM后，虽然模型的性能出现了一定的下降，但也没有改变边界平滑所起到的积极作用。

分析 

         《On calibration of modern neural networks》中指出，模型产生的预测置信度不太能代表真实的正确性概率（ poorly calibrated）。因此作者对加入边界平滑的模型这方面性能进行了验证，将预测出的实体按对应的置信度分为10组，然后计算每个组的精确度，如果模型具有较好的calibrated，即精确度应该接近每个组的置信度。结果如下所示：

        作者在CoNLL2003和OntoNotes5上进行了实验，可以看出加了边界平滑的模型具有更好的calibrate，也就是模型预测出的置信度与真实发生的概率是比较接近的。

        作者之前认为边界平滑可以去掉标注不一致所产生的噪声，但是在训练数据集中加入这样的边界噪声数据后，效果并没有得到明显的提升，因此作者对于该猜想并没有找到足够的证据（该部分也没有没实验数据展示）。

        作者在不同的平滑度下进行了实验：

        可以看出使用标准的交叉熵损失会比使用界平滑更加的sharp，从而导致找到的接近方案相对尖锐，而边界平滑可以达到一个平坦的最小值，而很多理论研究认为模型的平滑度是模型泛化的一个相关因素，这就能解释边界平滑带来的提升。

总结 

        作者通过将标记span周围的span分配一定的概率，来减弱模型的过拟合，在多个baseline上都有一定的提升。（感觉这个跟前面有篇two-stage的方法中为部分匹配的span分配权重来优化loss有点像？实验证明soft example对于模型性能也是有一定的提升的）