数据结构–字符串的朴素模式匹配算法

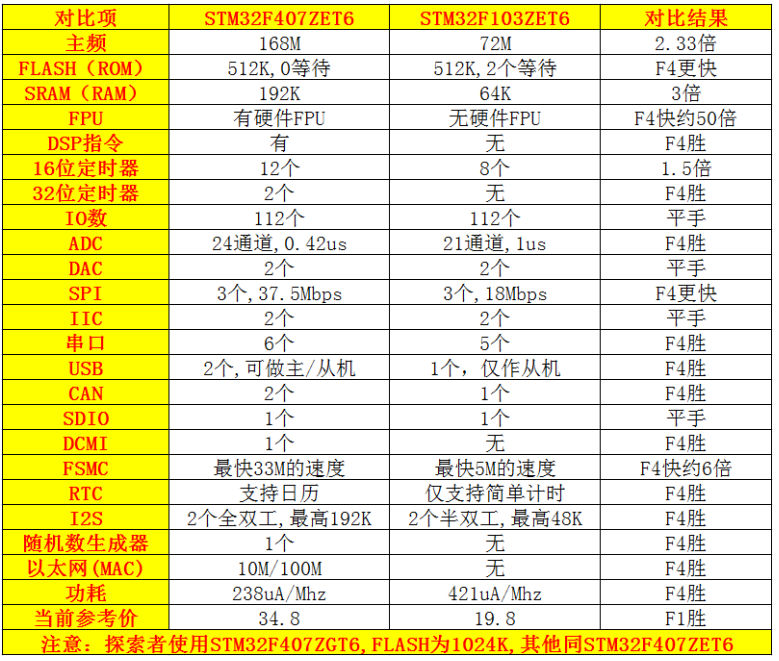
$主串：$
‘嘿嘿嘿红红火火恍恍惚惚嗨皮开森猴开森$笑出猪叫$哈哈哈哈嗨森哈哈哈哈哈哈嗝’
$模式串：$
$‘笑出猪叫’$

$子串--主串的一部分，一定存在$
$模式串--不一定能在主串中找到$

两种模式匹配算法

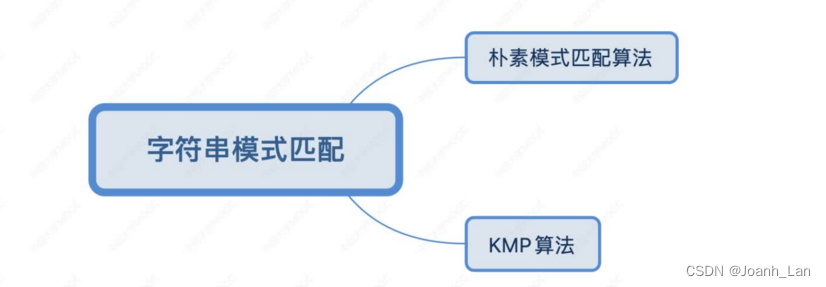
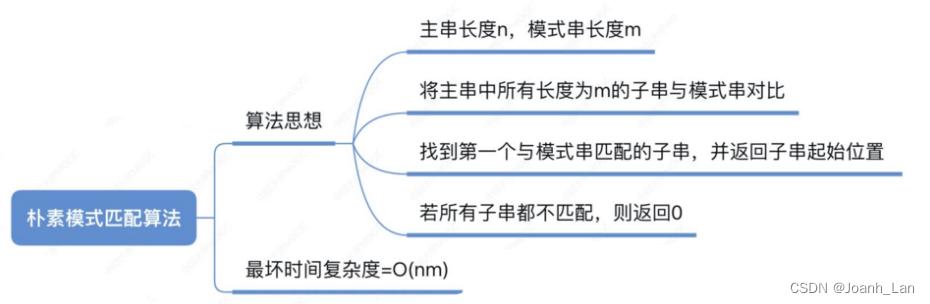
朴素模式匹配算法

… …

… …

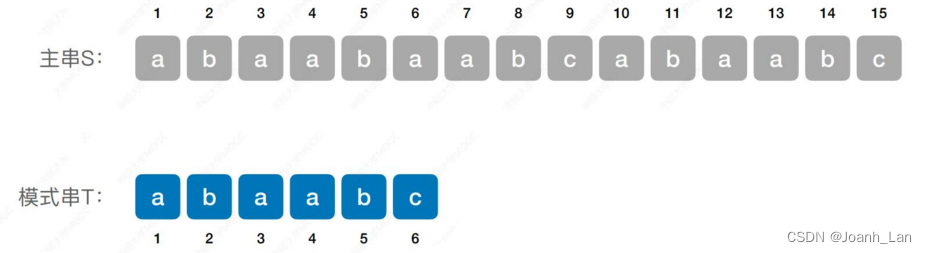
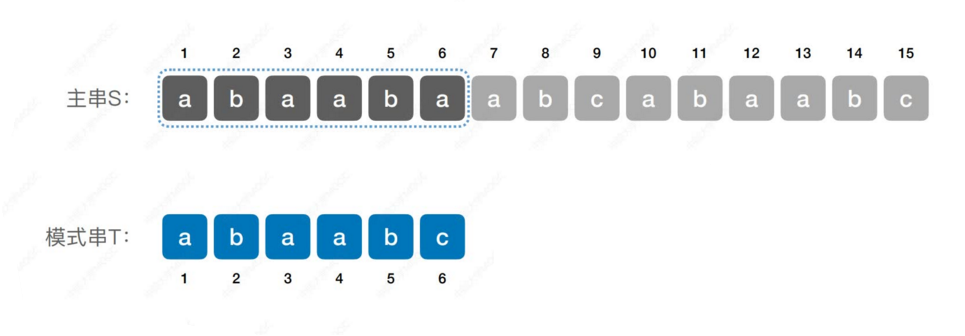
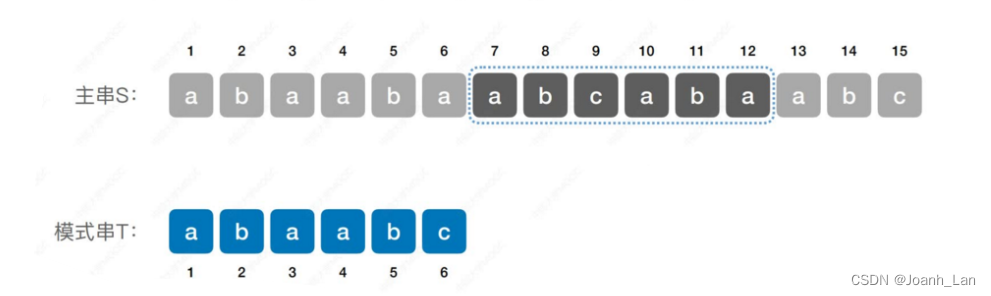
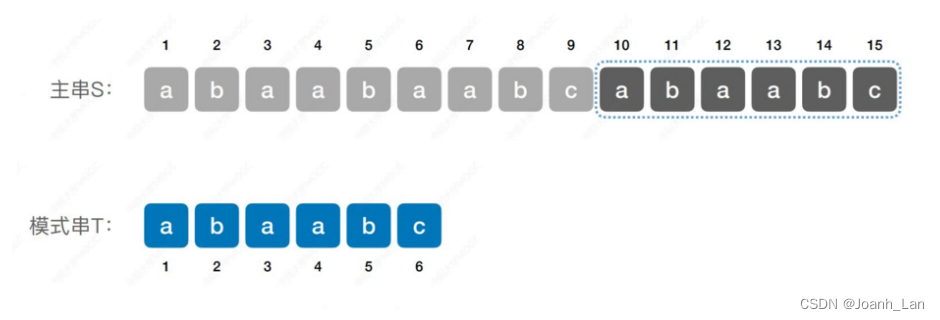
主串长度为n，模式串长度为m
$最多对比n-m+1个子串$
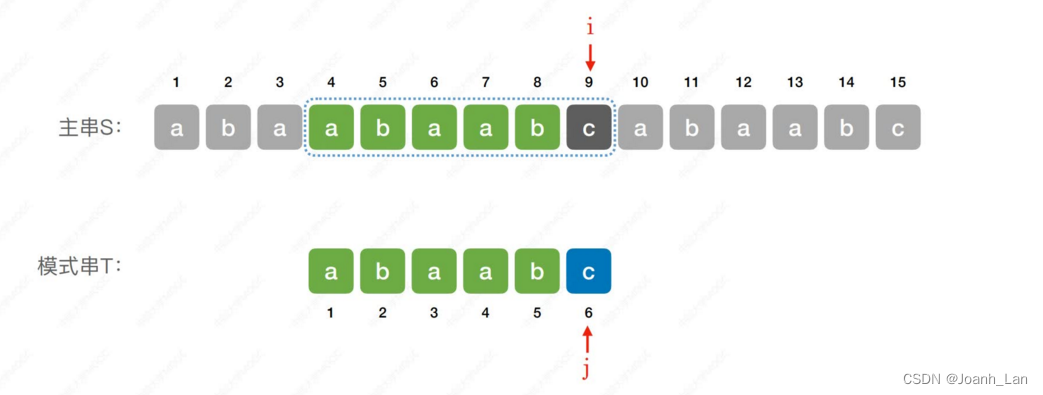
朴素模式匹配算法︰将主串中$所有长度为m的子串$依次与模式串对比，直到找到一个完全匹配的子串，或所有的子串都不匹配为止。

typedef struct
{
    char ch[15];
    int length;
}SString;

int Index(SString S, SString T)
{
    int i = 1, j = 1;
    while (i <= S.length && j <= T.length)
    {
        if (S.ch[i] == T.ch[j]) i++, j++;
        else    i = i - j + 2, j = 1;
    }

    if (j > T.length)
        return i - T.length;
    else 
        return 0;
}

时间复杂度

最坏时间复杂度= O(nm)

最坏的情况，每个子串都要对比 $m$ 个字符，共 $n-m+1$ 个子串，复杂度= $O((n-m+1)m)=O(nm)$
注:很多时候，n >> m

知识点回顾与重要考点