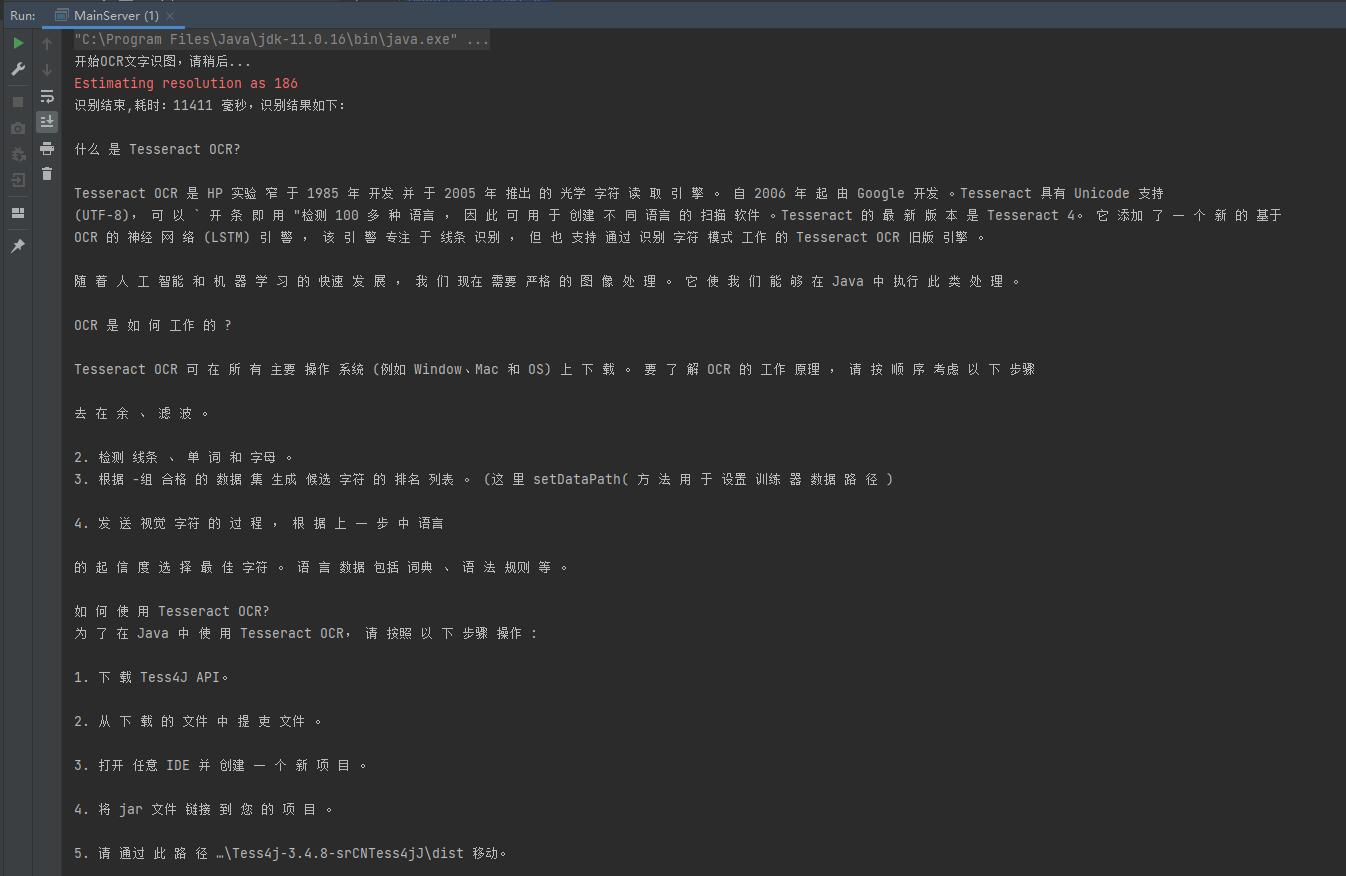
开裂
目录
k-雇佣农民
题目描述
输入描述:
输出描述:
输入
输出
备注:
小e的苹果树
不降序列
k-雇佣农民
题目描述
Ly很喜欢星际争霸二这款游戏,但是他现在玩不到了。所以Ly现在只能做一个关于农民的题消磨时光。
开始时Ly没有任何农民,第i天白天Ly最多可以雇佣i个农民,Ly所雇佣的每个农民每天晚上可以生产出1块矿石。Ly想知道他雇佣的农民生产恰好n块矿石最少需要多少天以及雇佣农民的方案。
输入描述:
第一行包含一个非负整数n。
输出描述:
输出两行分别表示最少天数和购买方案。 第一行为一个整数t表示最少天数。 第二行包含用空格隔开的t个整数,第i个整数表示第i天白天雇佣农民的数量。如果有多种方案,输出在越早的时间雇佣农民尽量多的方案。 如果无解则直接只输出一个-1即可。
示例1
输入
5
输出
3 1 1 0
备注:
n<=10^15
思路:
不难发现,增长程度是1,3,6,10......因此,不妨假设每天都雇佣满,那么总贡献就会一直按照前面的累加,这样其实就能得出一共要雇佣几天出来。当雇佣天数出来之后,我们只需要去拼凑每天的雇佣人数就能得出答案,第i天的雇佣贡献是 (总天数-第i天 +1)* 当天雇佣人数;
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<cstring>
#include <unordered_set>
//#include<priority_queue>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;
ll INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// int get_len(int x1,int y1,int x2,int y2)
// {
// return (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1);
// }
const ll N = 2e6+ 10;
const ll mod =998244353;
ll t,n,m,x,y,ca;
ll arr[N],brr[N],crr[N];
// int h[N],ne[N],e[N],w[N],idx;
void fatchuan()
{
cin >> n;
ll day = 0;
ll ant = 0;
ll val = 1;
ll v = 1;
while(ant <= n)
{
day ++;
ant += val;
v ++;
val += v;
}
cout << day <<endl;
rep(i,1,day)
{
cout << min( i, n / (day - i +1))<<' ';
n -= (day - i + 1) * min( i, n / (day - i +1));
}
}
int main()
{
IOS;
t=1;
//scanf("%d",&t);
//cin>>t;
ca=1;
while(t--)
{
fatchuan();
ca++;
}
return 0;
}
小e的苹果树

思路:
通过优先队列来进行动态选择是否摘苹果
#include<bits/stdc++.h>
#define ll long long
#define lowbit(x) (x&(-x))
#define rep(x,a,b) for(int x=a;x<=b;x++)
#define pre(x,a,b) for(int x=a;x>=b;x--)
#define ac puts("Yes")
#define wa puts("No")
#define endl "\n"
#define pb push_back
#define pii pair<ll,ll>
#define de cout<<1;
#define mem(a,x) memset(a,x,sizeof a)
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int mod1=998244353;
const int mod2=1e9+7;
const int N=3e5 + 10 + 60;
ll n, m, ans;
int number;
ll x[N];
void solve()
{
cin >> n >> m;
vector<int>p[n + 1];
map<int, int>mp;
rep(i, 1, n)
{
cin >> x[i];
mp[x[i]] = i;//并不是按照顺序输入,因此,进行了类似离散处理
ll num;
cin >> num;
rep(j, 0, num - 1)
{
ll y;
cin >> y;
p[i].push_back(y);
}
sort(p[i].begin(), p[i].end());//苹果高度也不是有序输入,输入之后进行排序
}
ll ans = 0;
priority_queue<int>q;
ll res = 0;
ll last = 0;//当前位置
for(auto i : mp)
{
ll x = i.first, y = i.second;// x 苹果树的位置 ,y 从0开始是第几个苹果树
m -= (x - last);//cout<<m;
last = x;
while(m < 0 && q.size())//如果此时时间已经用完了,那就把时间还回去,这个苹果不摘了
{
m += q.top();
q.pop();
ans -- ;
res = max(res, ans);
}
if(p[y].size())//判断是否存在,否则会re
rep(j, 0, p[y].size() - 1)
{
if(m >= p[y][j]) m -= p[y][j], q.push(p[y][j]), ans ++, res = max(res, ans);
else
{
if(q.size() > 0)
if(q.top() > p[y][j]) m += q.top(), m -= p[y][j], q.pop(),q.push(p[y][j]);
}
res = max(res, ans);
}
}
cout << res;
}
int main()
{
IOS;
int t;
//cin >> t;
t = 1;
while(t -- )
{
number++;
solve();
}
return 0;
}
不降序列
思路:
对于任意一个数,如果要修改使得权值尽可能的大,即要将它变为。这种操作下同删除这个数字的结果是一样的,因此我们只需要进行删除操作即可。利用即可,其中i表示了当前数的位置,j表示了当前总共的操作数。对于每次操作,我们删除当前位置之前的一个数。则状态转移方程为其中len为此时进行的操作数(如果len = 2 则删除前面两个数)
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<cstring>
#include <unordered_set>
//#include<priority_queue>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;
ll INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// int get_len(int x1,int y1,int x2,int y2)
// {
// return (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1);
// }
const ll N = 2e6+ 10;
const ll mod =998244353;
ll t,n,m,x,y,ca;
ll arr[N],brr[N],crr[N];
// int h[N],ne[N],e[N],w[N],idx;
ll dp[600][600];
void fatchuan()
{
ll k;
cin >> n >> k;
rep(i,1,n)
{
cin >> arr[i];
}
memset(dp,-1,sizeof(dp));
dp[1][0] = 0;
rep(i,2,n)
{
rep(j,0,k)
{
if(i - j < 2)continue;
rep(k,0,j)
{
ll len = j - k;
if(i - len >= 2)
{
dp[i][j] = max(dp[i][j] , dp[i - len - 1][j - len] + (ll)(arr[i] - arr[i - len - 1]) * (arr[i] - arr[i - len - 1]));
}
}
}
}
ll ans =0;
rep(i,0,k)
{
ans = max( ans, dp[n][k]);
}
cout<<ans;
}
int main()
{
IOS;
t=1;
//scanf("%d",&t);
//cin>>t;
ca=1;
while(t--)
{
fatchuan();
ca++;
}
return 0;
}








![[ 云计算 | AWS ] IAM 详解以及如何在 AWS 中直接创建 IAM 账号](https://img-blog.csdnimg.cn/ed181100df55439aa74eba1c99996a04.png)