CF578A(直线方程 + 数学) 1700

有一条折线 ， 这个折线经过这样一组点：

(0,0) - (x,x) - (2x,0) - (3x,x) - (4x,0) - ....

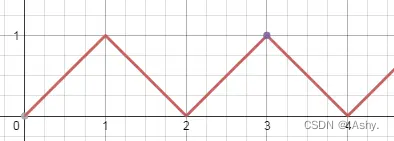
现给出折线上一点 ， 求 x 的最小值

思路：我们不妨用解方程的思想 ，先写出折线的方程（y = kt + b）, 然后解方程

上升段：

$$y=t-2kx(k=0,1,2,\mathrm{3....})$$

$$x=\frac{t-y}{2k}(k=0,1,2,\mathrm{3....})$$

下降段：

$$y=-t+2kx(k=1,2,\mathrm{3....})$$

$$x=\frac{t+y}{2k}(k=1,2,\mathrm{3....})$$

由于 t 与 y 已知(输入量) , 要想让 x 最小 ， 使得 k 最大即可 ， 所以问题转化为如何求 k。

在图像中 ，x 为纵坐标的最高点 ， 因此还需要满足

$$\frac{t+y}{2k}\ge y$$

k ≥ 1 时

$$k\le \frac{t+y}{2y}$$

我们上面分析过了 ， 要取最大值 ， 即若

$$\frac{t+y}{2y}\ge 1$$

则有解 ， 分别带入上升段和下降段求最小值即可

当 k = 0 时 显然 y = t

显然 当 x = t 的时候 x 最小。

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e5+10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;
const int inf = 1 << 31 - 1;
const double eps = 1e-9;

double x , y , k , ans = inf; 

signed main(){

	cout << fixed << setprecision(10);

	cin >> x >> y;
	
	if(x == y) ans = x;
	else{
		k = (x - y) / (2 * y);
		k = (int) k;
		if(k >= 1) ans = (x - y) / (2 * k);
		
		k = (x + y) / (2 * y);
		k = (int) k;
		if(k >= 1) ans = min(ans , (x + y) / (2 * k));	
	}
	
	if(ans == inf) cout << "-1"; 
	else cout << ans ;
	

	return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);