DAY35：贪心算法（二）分发饼干+摆动序列

news2024/9/29 9:36:24

文章目录

    • 455.分发饼干
      • 思路
      • 两个for循环嵌套的写法
        • 为什么这种写法必须要有visited数组
        • debug测试
        • 逻辑问题：没有进行计数
        • 逻辑问题：找到了result=3个孩子
      • 一层for循环的写法
        • 为什么这种写法一定要把小孩数组放在外面
    • 376.摆动序列（逻辑问题）
      • 思路
      • 如何判断摆动
      • 特殊样例：相邻元素相同
      • 特殊样例：首尾元素
      • 最开始的写法
      • 第一次修改：卡住很久，最后发现是不能默认最左侧峰值存在的
      • 正确修改
      • 逻辑问题总结

455.分发饼干

  • 重点在于掌握两层for循环嵌套的时候必须visited数组记录的问题，以及如何一层for循环解决满足条件才移动这种问题。

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

  • 1 <= g.length <= 3 * 10^4
  • 0 <= s.length <= 3 * 10^4
  • 1 <= g[i], s[j] <= 2^31 - 1

思路

输入两个数组分别是小孩的胃口g和饼干的大小s，饼干大小g[i]必须>小孩子的胃口s[i]才能满足小孩。

我们需要在数组g里面，满足尽量多的小孩，也就是较大的g[i]值，最好对应较大的s[i]值，才算不浪费g[i]。

因此，沿着这个思路分析，为了让尽可能多的g[i]得到满足（s[i]>=g[i]），每次的局部最优就是找到最大的s[i]，也就是找到最大的饼干，先分给胃口最大的g[i]。全局最优，就是我们可以喂饱最多的小孩子的数量。

当我们发现这个局部最优好像能够推出全局最优，同时又找不到反例的话，就可以尝试贪心。

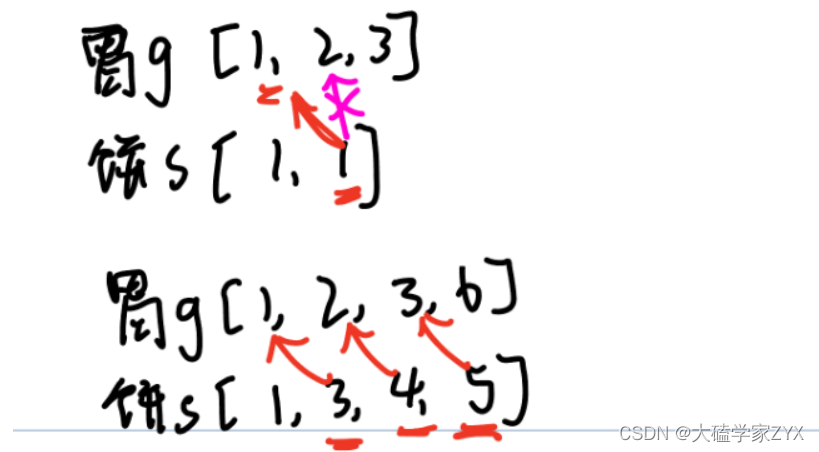
在这里插入图片描述
大致思路：先找s数组里面较大的数值，再在g数组里面找满足s[i]>g[i]的最大数值。

两个for循环嵌套的写法

  • 饼干的遍历需要条件进行控制，也就是说如果饼干过小满足不了小孩子的胃口，是不能继续遍历饼干的，但是需要继续遍历小孩子！
  • 基于贪心的策略，我们优先保证大饼干供应g[i]比较大的孩子，因此sort可以直接降序排列，或者for循环倒着遍历
  • 两个for循环嵌套的写法需要注意，由于两个for嵌套，每次外面的for循环数值加1，里面这层for都会从头开始遍历一遍，因此这种情况必须要统计里面的for哪些已经被遍历过了，否则就会反复遍历内层循环的同一个数值！这类似回溯递归中的i=startIndex的用法，为的就是不在内层遍历同样的元素！
//先对小孩胃口数组和饼干数组排序
class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        //排序，默认升序
		sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        int result = 0;//记录喂饱了多少小孩
        //两个for循环，记录小孩子已经被投食
        vector<bool>visited(g.size(),false);
        
        //开始遍历，孩子胃口从大到小遍历,饼干也从大到小遍历
        //注意，如果饼干没有投喂成功的话，是不能向前遍历的！
        for(int i=s.size()-1;i>=0;i--){
            //小孩是内部循环，所以需要标记已经被遍历过的小孩子
            for(int j=g.size()-1;j>=0;j--){
                if(s[i]>=g[j]&&visited[j]!=true){
                    result +=1;
                    //标记这个小孩已经被投食
                    visited[j]=true;
                    break;
                }
                else{
                    continue;
                }
            }
        }
        return result;
        
    }
};

为什么这种写法必须要有visited数组

两个for嵌套，每次外面的for循环数值加1，里面这层for都会从头开始遍历一遍。

因此这种情况，如果不想内层反复从头遍历一整遍，必须要统计里面的for哪些已经被遍历过了，否则就会反复遍历内层循环的同一个数值！这类似回溯递归中的i=startIndex的用法，为的就是不在内层遍历同样的元素！

例如下图的红色箭头和绿色箭头，有了红色箭头之后必须排除绿色箭头二次遍历的情况。

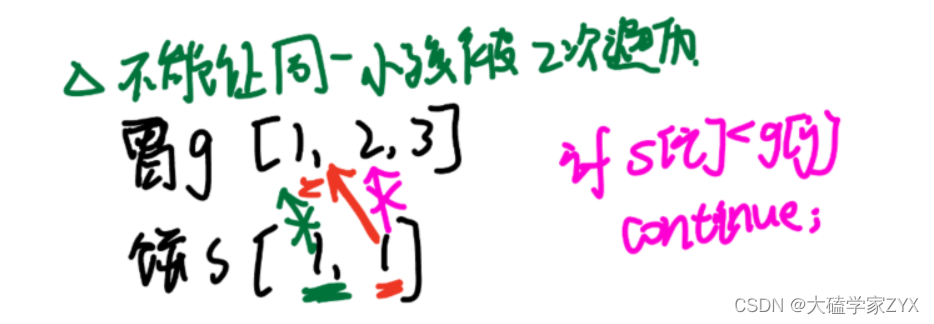
在这里插入图片描述

debug测试

逻辑问题：没有进行计数

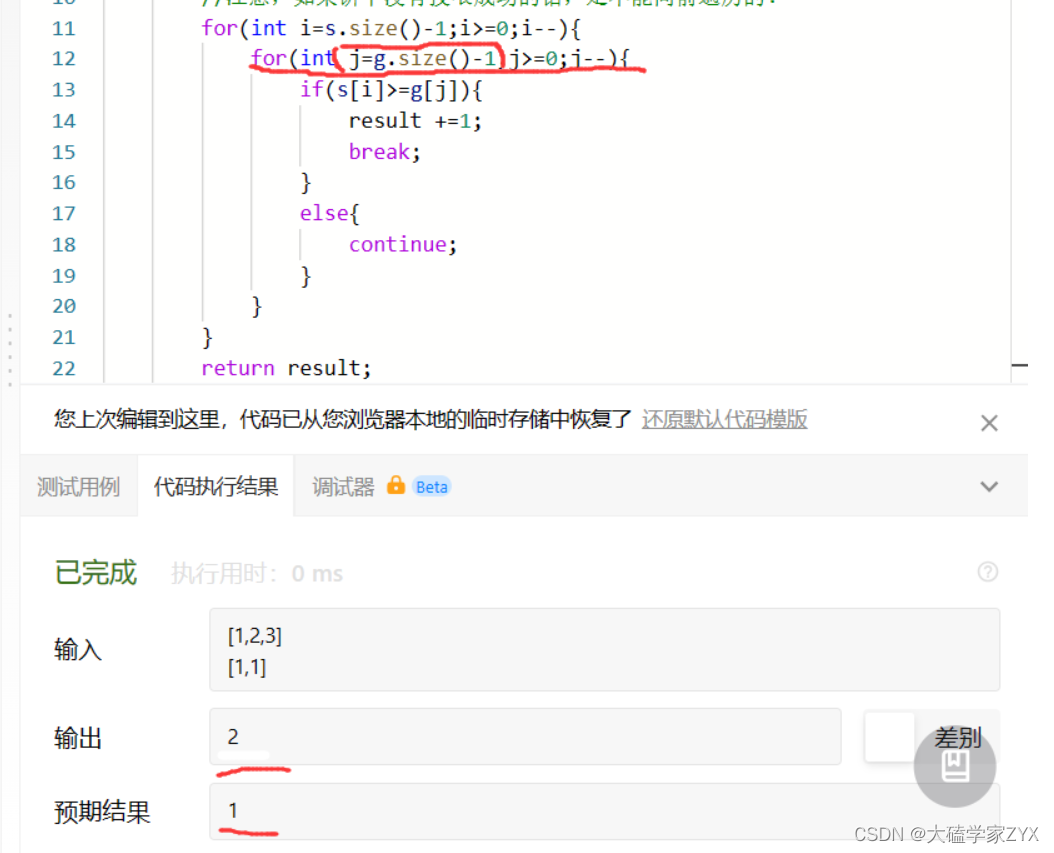
在这里插入图片描述
最开始采用两层for循环的写法的时候，没意识到实际上每次外层变化，内层都会被从头开始遍历一遍！

因此内层为了不重复遍历，必须用visited数组来防止内层被遍历很多遍。加上数组之后就避免了内层重复遍历问题

逻辑问题：找到了result=3个孩子

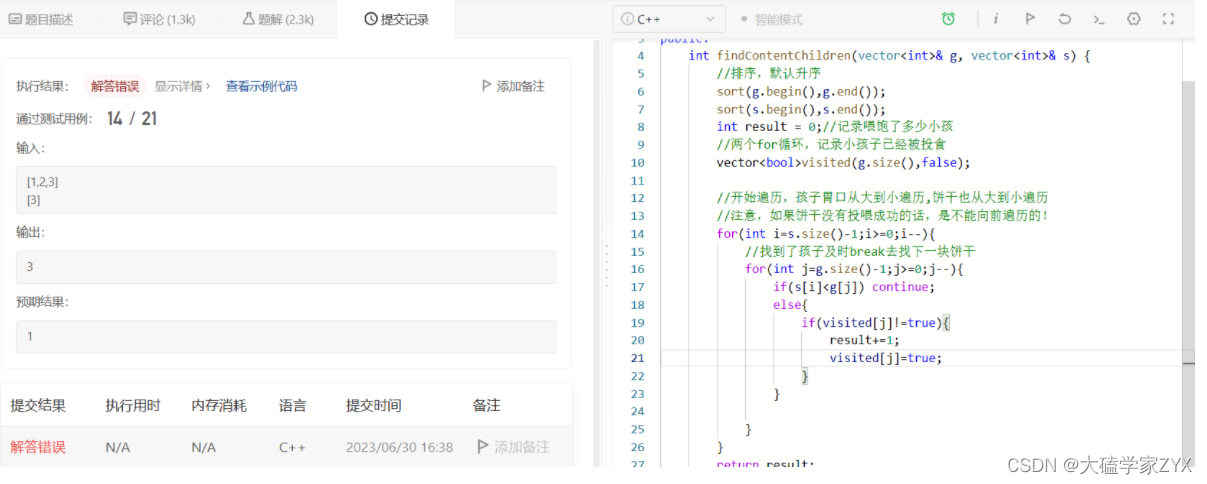
在这里插入图片描述

在这种写法中，一个饼干找到了配套的孩子之后，内层孩子g的for循环没写break，没有break也就意味着一块饼干找到了孩子之后，不能及时遍历下一块饼干。

我们修改方式是在内层循环最后加上break。

一层for循环的写法

两层的写法实际上考虑复杂了，也可以只写一层for循环。

一层for循环的写法，就是针对小孩的胃口做遍历。

  • 减少一层for循环的技巧在于，用了一个 index 来控制饼干数组的遍历，遍历饼干并没有再起一个 for 循环，而是采用自减的方式，这也是常用的技巧！
class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        //排序，默认升序
		sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        int result = 0;//记录喂饱了多少小孩
        int index = s.size()-1;

        //开始遍历，孩子胃口从大到小遍历,饼干也从大到小遍历
        for(int i=g.size()-1;i>=0;i--){
            if(index>=0&&g[i]<=s[index]){
                result += 1;
                index--;
            }
        }
        return result;
    }
};

为什么这种写法一定要把小孩数组放在外面

因为index做指针这种for写法，外面的 for 里的下标 i 是固定移动的，而 if 里面的下标 index 是符合条件才移动的。

也就是说，下面这种情况，当饼干数组不符合条件的时候，小孩数组继续移动，但是饼干数组在不满足if条件的时候，index不变，也就是不移动！

输入: g = [1,2,3], s = [1,1]
输出: 1

这是不用两层for循环+continue的情况下，能够让饼干数组满足条件才移动的重要技巧！

那么为什么不能用for遍历饼干，if遍历小孩，示例如下：

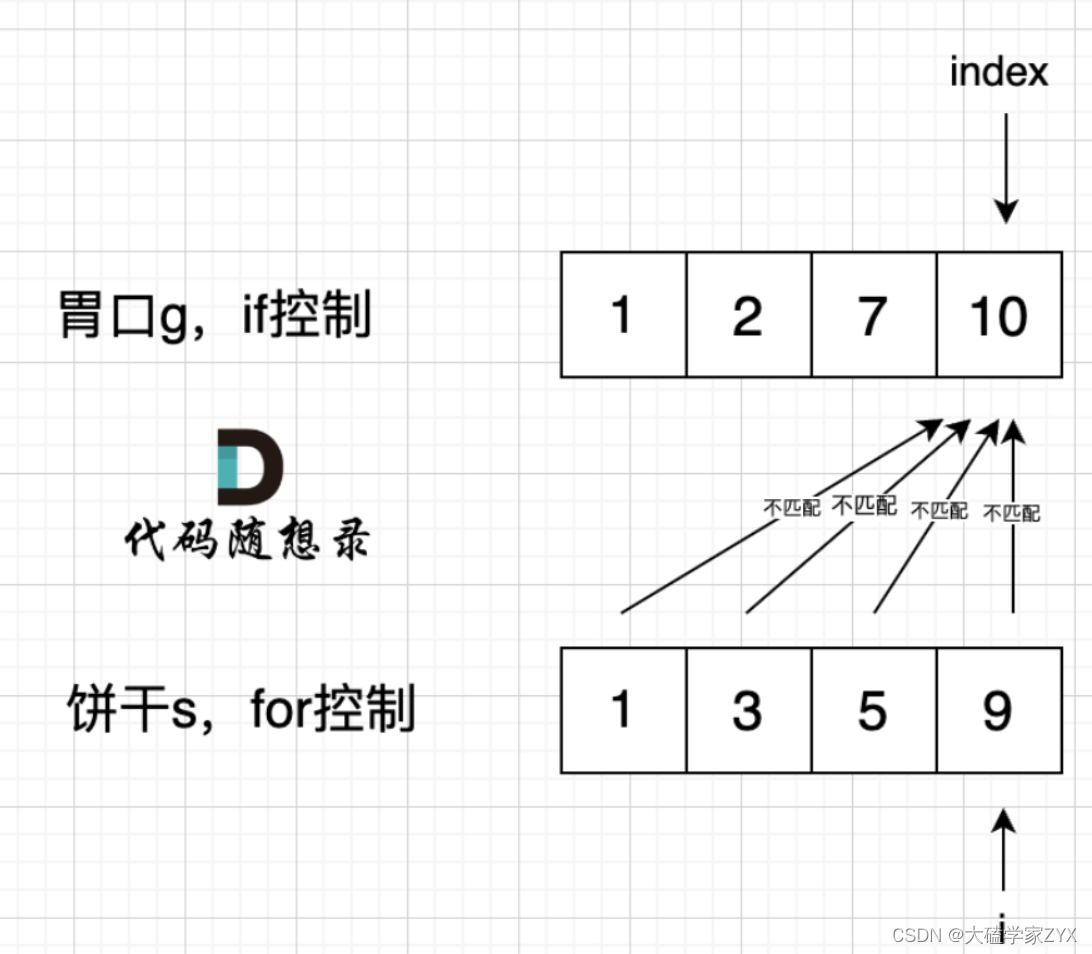
在这里插入图片描述
if 里的 index 指向 胃口 10， for 里的 i 指向饼干 9，因为 饼干 9 满足不了 胃口 10，所以 i 持续向前移动，而 index 走不到s[index] >= g[i] 的逻辑，所以 index 不会移动，那么当 i 持续向前移动，最后所有的饼干都匹配不上。

所以 一定要 for 控制 胃口，里面的 if 控制饼干，防止这种第一个小孩胃口过大，结果所有的饼干遍历完了都没有能匹配的情况。

376.摆动序列（逻辑问题）

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

思路

首先要理解摆动序列的含义，如下图所示。

相当于是通过删除元素，使得原有序列变为摆动子序列，并求出摆动子序列最大长度。

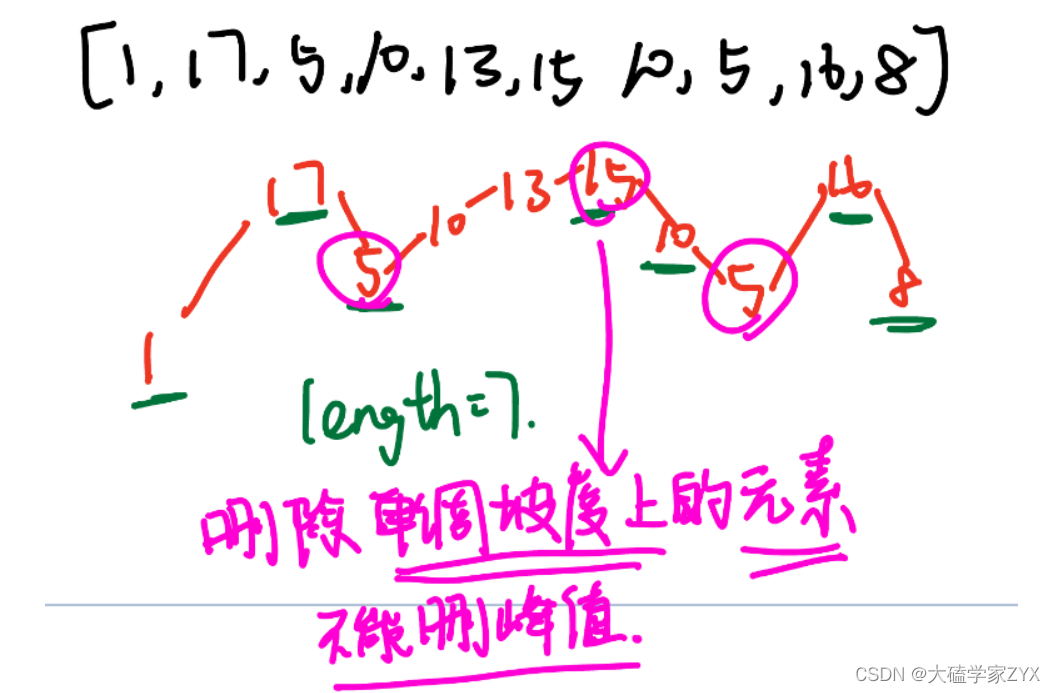
在这里插入图片描述
局部最优是删除单调坡度上的元素，使得这个坡度多出两个局部峰值；全局最优是峰值最多。

局部最优能推出全局最优，因此可以考虑贪心。

但是本题中我们不需要把多出来的元素都删掉！因为数组删除元素本身就是一个O(n)的操作（要先查询到元素位置），因此没必要真的做删除元素的操作！

实际上代码实现，只需要定义变量，遇到峰值做++，没有峰值就不做++即可。因此本题不用删除元素！删除元素会增加复杂度！

如何判断摆动

我们定义一个之前的差值pridiff = nums[i]-nums[i-1]; 之后的差值curdiff = nums[i+1]-nums[i]

如果pridiff和curdiff一正一负，就说明是摆动，需要做++操作。只要节点两侧差值不一样，就说明这个节点是摆动峰值

if (prediff>0&&curdiff<0||prediff<0&&curdiff>0)  result++;

特殊样例：相邻元素相同

题目中没有说相邻元素一定不同，因此还要考虑平坡情况，也就是pridiff = 0或者curdiff= 0。

如果只取平坡右边的值：

if (prediff=0&&curdiff>0||prediff=0&&curdiff<0)  result++;

特殊样例：首尾元素

首尾元素都算作坡度，因此需要对首尾元素单独处理，因为首元素不存在prediff而末尾元素不存在curdiff

可以直接写死，遍历的时候不从第一个而是从第二个开始，并且不遍历最后一个，防止数组越界。

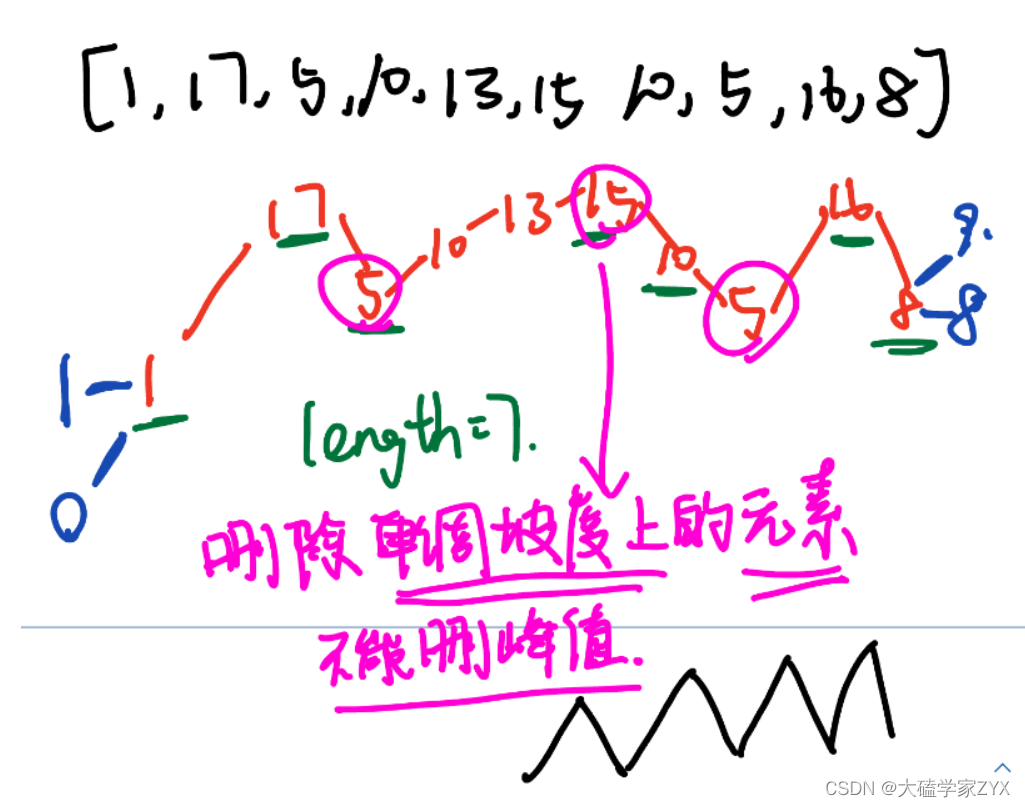
因为最开始和最后默认各有一个峰值，即使是前后相等，也不影响峰值的存在！

比如说下图蓝色字体的部分，即使数组前后加上了数字，也不影响峰值判断。

在这里插入图片描述

最开始的写法

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
		int prediff = 0;
        int curdiff = 0;
        if(nums.size()==1)  return 1;
        if(nums.size()==2){
            if(nums[0]!=nums[1]) return 2;
            else return 1; 
        }
        int result = 2;//针对数组长度大于2的情况
        for(int i=1;i<num.sise()-2;i++){
            prediff = nums[i]-nums[i-1];
            curdiff = nums[i+1]-nums[i];
            //平坡取最右边元素，可以合并
            if((prediff>=0&&curdiff<0)||(prediff<=0&&curdiff>0)){
                result++;
            }
        }
        return result;
        
    }
};

这种写法忽略了一个问题，就是数组里所有的元素可能都相等！造成如下图逻辑问题，也就是说，我们的result初始值不能是2，必须是1.

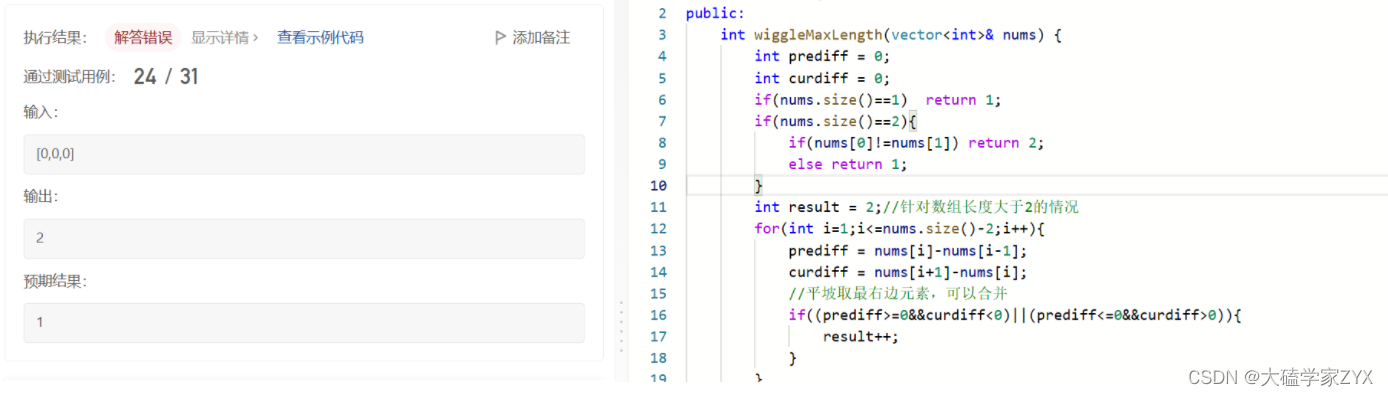
在这里插入图片描述
result初始值不能是2，必须是1的话，意味着左右两个峰值，不能同时默认存在，需要在逻辑里加上首/尾峰值元素的判断。

因此针对这种写法做了以下修改：

第一次修改：卡住很久，最后发现是不能默认最左侧峰值存在的

  • 因为数组里的元素可能都相等，所以初值result必须=1；此时，就需要单独有处理首尾的逻辑，否则首尾两个峰值一定会漏掉一个。
  • 首尾两个峰值，从i=0开始还是i=1开始也很重要。下面这种写法从i=1开始，就是注定无解的。
  • 必须从i=0开始，因为只有prediff能用curdiff来表示，而curdiff是不能用prediff来表示的！在数值往前遍历的过程中，prediff = curdiff，从而能够免去nums[i]-nums[i-1]的情况。
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
		int prediff = 0;
        int curdiff = 0;
        if(nums.size()==1)  return 1;
        if(nums.size()==2){
            if(nums[0]!=nums[1]) return 2;
            else return 1; 
        }
        //针对数组长度>=3的情况，但是我们还要考虑，数组里全是相等元素的情况，所以result初值不能是2，应该是1
        //默认序列最左边有一个峰值，最右边峰值通过curdiff修改来取，因为最右边没有i+1
        int result = 1;
        for(int i=1;i<=nums.size()-2;i++){
            prediff = nums[i]-nums[i-1];
            curdiff = nums[i+1]-nums[i];
            //平坡取最右边元素，可以合并
            if((prediff>=0&&curdiff<0)||(prediff<=0&&curdiff>0)){
                result++;
            }
        }
        return result;
        
    }
};

正确修改

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
		int prediff = 0;
        int curdiff = 0;
        if(nums.size()==1)  return 1;
        if(nums.size()==2){
            if(nums[0]!=nums[1]) return 2;
            else return 1; 
        }
        //针对数组长度>=3的情况，但是我们还要考虑，数组里全是相等元素的情况，所以result初值不能是2，应该是1
        //默认序列最右边有一个峰值
        int result = 1;
        for(int i=0;i<=nums.size()-2;i++){
            curdiff = nums[i+1]-nums[i];
            if((prediff >= 0 && curdiff < 0) || (prediff <= 0 && curdiff > 0)){
                result++;
                prediff = curdiff;
            }
        }
        return result;
        
    }
};

逻辑问题总结

包含左侧峰值逻辑的示意图如下：
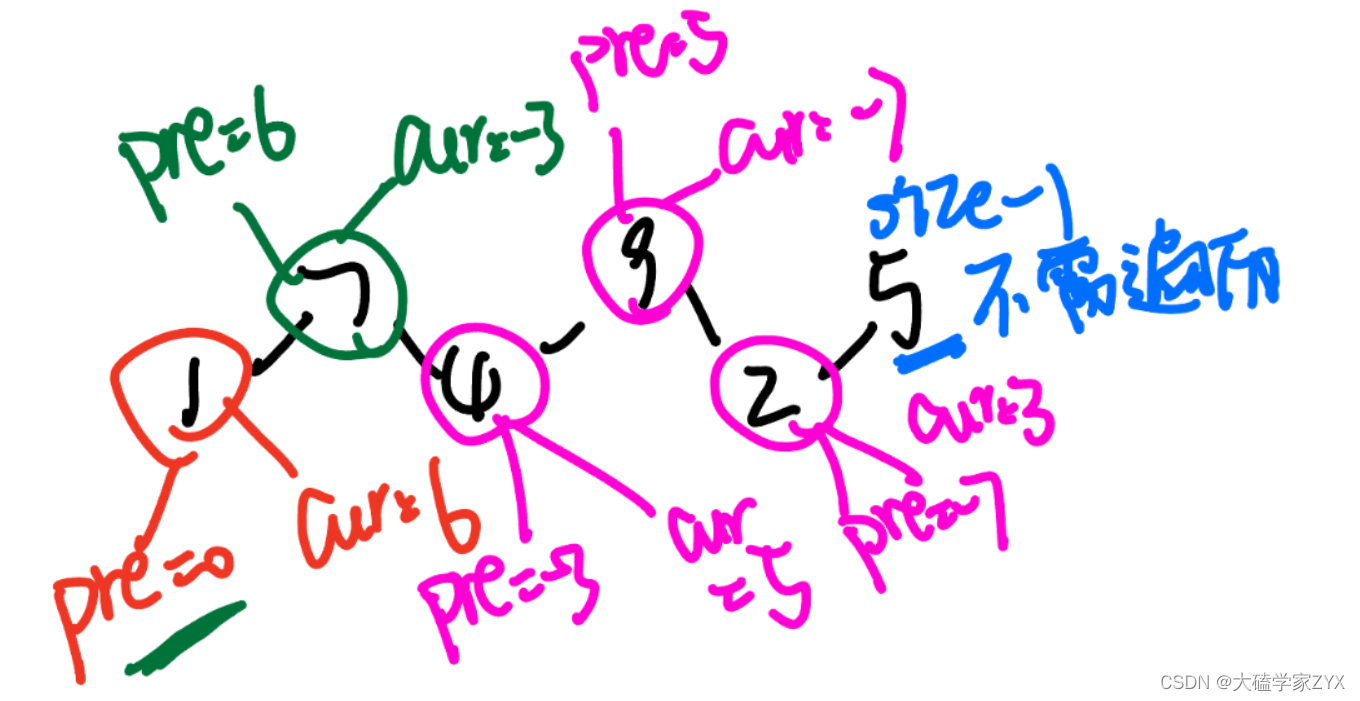
在这里插入图片描述

这道题的核心在于，pre可以继承cur的值，但是cur不能继承pre的值！卡住的原因就是因为没想明白这一点，从i=1开始遍历，无论怎样的继承方式，都不能把所有元素都遍历全。

因此在首尾两个峰值必须二选一留下来，也就是for循环，i=0还是i=1的选择时，必须从i=0开始，也就是默认初始存在的峰值是最右侧的峰值，而不是最左侧的峰值。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/711713.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

02_04实时调度类及SMP多核处理器的实时操作系统体系结构

02_04实时调度类及SMP多核处理器的实时操作系统体系结构

上一篇文章说的是普通进程的调度但同时还有实时进程在linux上面进行运行 这边来看看实时进程在linux里面怎么调度 同时linux操作系统对实时任务的处理方式和设计思想 实时调度类 Linux进程分为两大类:实时进程和普通进程。 实时进程与普通进程根本不同之处&#xff0c;如果系…
阅读更多...
ModuleNotFoundError: No module named ‘transformers_modules.chatglm2-6b‘解决方案

ModuleNotFoundError: No module named ‘transformers_modules.chatglm2-6b‘解决方案

大家好，我是爱编程的喵喵。双985硕士毕业，现担任全栈工程师一职，热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…
阅读更多...
青少年机器人技术一级核心知识点：机械结构及模型（四）

青少年机器人技术一级核心知识点：机械结构及模型（四）

随着科技的不断进步&#xff0c;机器人技术已经成为了一个重要的领域。在这个领域中&#xff0c;机械结构是机器人设计中至关重要的一部分&#xff0c;它决定了机器人的形态、运动方式和工作效率。对于青少年机器人爱好者来说&#xff0c;了解机械结构的基础知识&#xff0c;掌…
阅读更多...
LabVIEW大模拟数据解决方案

LabVIEW大模拟数据解决方案

LabVIEW大模拟数据解决方案 比亚迪汽车对于在动力总成标定和控制部门工作的400多名工程师来说&#xff0c;这种投资包括实现NI的新战略和解决方案&#xff0c;以更好地捕获和管理大量的原始测试数据&#xff0c;在车辆上市前做出更明智的决策。 因为能够更好地获取更优质的数…
阅读更多...
Go语言开发者的Apache Arrow使用指南：内存管理

Go语言开发者的Apache Arrow使用指南：内存管理

如果你看了上一篇《Go语言开发者的Apache Arrow使用指南&#xff1a;数据类型》[1]中的诸多Go操作arrow的代码示例&#xff0c;你很可能会被代码中大量使用的Retain和Release方法搞晕。不光大家有这样的感觉&#xff0c;我也有同样的feeling&#xff1a;**Go是GC语言[2]&#x…
阅读更多...
MWCS 2023，到底有些啥？（下篇）

MWCS 2023，到底有些啥？（下篇）

█ 亚信科技 5G行业专网一体机&#xff1a; 反光太厉害了&#xff0c;看不太清&#xff1a; 这几张都是小枣妹拍的&#xff0c;^_^&#xff1a; █ 浩鲸科技 浩鲸&#xff0c;就是以前的中兴软创&#xff1a; █ 紫光展锐 6G这块&#xff0c;干货很多&#xff1a; 这次重点展示…
阅读更多...
docker容器日志占满硬盘空间的解决方案

docker容器日志占满硬盘空间的解决方案

目录 原因分析解决方案方案一 定时清空日志文件方案二 全局容器日志大小方案三 修改日志驱动 docker常用清理空间命令 原因分析 由于默认情况下&#xff0c;docker使用json-file类型的日志驱动&#xff0c;该日志驱动默认情况下&#xff0c;每个容器的日志会一直追加在文件名为…
阅读更多...
chatgpt赋能python：用Python模拟用户登录，实现多个网站的SEO优化

chatgpt赋能python：用Python模拟用户登录，实现多个网站的SEO优化

用Python模拟用户登录&#xff0c;实现多个网站的SEO优化 介绍 在互联网时代&#xff0c;SEO已成为许多网站提高曝光率和流量的重要手段之一。而SEO优化的一个重要方面就是网站的用户登录。然而&#xff0c;手动登录多个网站进行SEO操作是非常耗时耗力的。那么&#xff0c;有…
阅读更多...
卷积神经网络实现猫狗分类

卷积神经网络实现猫狗分类

目录 一、环境配置二、神经网络CNN1、简介2、CNN结构3、层次说明 三、数据集准备1、下载数据集2、数据集分类 四、 猫狗分类的实例——基准模型1、构建网络模型2、配置训练方法3、转换格式4、模型训练并保存生成的模型5、结果可视化 五、调整基准模型1、图像增强2、增强后的图像…
阅读更多...
【C语言初阶（8）】函数1

【C语言初阶（8）】函数1

文章目录 1. 函数的介绍2. 函数的分类2.1 库函数2.2 自定义函数 3. 函数的参数4. 函数的调用4.1 传值调用4.2 传址调用 1. 函数的介绍 1. 什么是函数&#xff1f; 函数是完成特定任务的独立程序代码单元。语法规则定义了函数的结构和使用方式。 一些函数执行某些动作&#xff…
阅读更多...
Guava 之 EventBus

Guava 之 EventBus

​​EvenBus​​​ 是 Guava 中 Pub/Sub 模式的轻量级实现。平时开发如果我们要实现自己的 Pub/Sub 模型&#xff0c;要写不少类&#xff0c;设计也挺复杂&#xff0c;对业务代码也有一定的侵入&#xff0c;但是在使用了 ​​EventBus​​ 之后就很方便了。 在 Pub/Sub 模式中…
阅读更多...
Java——《面试题——tomcat篇》

Java——《面试题——tomcat篇》

全文章节 Java——《面试题——基础篇》 Java——《面试题——JVM篇》 Java——《面试题——多线程&并发篇》 Java——《面试题——Spring篇》 Java——《面试题——SpringBoot篇》 Java——《面试题——MySQL篇》​​​​​​ Java——《面试题——SpringCloud》 Java——…
阅读更多...
干货 | 智慧教育平台生成式人工智能应用的安全要求

干货 | 智慧教育平台生成式人工智能应用的安全要求

以下内容整理自清华大学《数智安全与标准化》课程大作业期末报告同学的汇报内容。 第一部分&#xff1a;编制说明 标准制定的基本原则主要包括以下四个方面&#xff1a; 综合性&#xff1a;本标准全面漫盖了智慧教育平台ChatGPT安全保护的要求&#xff0c;以便用户参考&#xf…
阅读更多...
Spring：Bean

Spring：Bean

Bean 概述配置方式自动装配继承与依赖作用域外部属性文件的使用 概述 Spring 容器负责管理依赖注入&#xff0c;它将被管理的对象都称为 bean 。我们通过 xml 文件配置方式进行对 bean 的声明和管理。 写法如下&#xff1a; <beans><bean id"bean的唯一标识符…
阅读更多...
Scrapy框架--CrawlSpider （详解+例子）

Scrapy框架--CrawlSpider （详解+例子）

目录 CrawlSpider 简介 基本运行 特性和概念 基本使用 创建CrawlSpider 运行 使用CrawlSpider中核心的2个类对象 Rule对象 LinkExtractors 作用 使用 查看效果-shell中验证 示例 注意 CrawlSpider 简介 CrawlSpider 是 Scrapy 框架提供的一个特殊的 Spider 类…
阅读更多...
Jvm内存模型剖析优化-JVM（四）

Jvm内存模型剖析优化-JVM（四）

上篇文章代码实例详解如何自定义双亲委派&#xff0c;主要实现ClassLoader&#xff0c;有两个方法&#xff0c;一个直接loadClass用父类的&#xff0c;如果想在破坏&#xff0c;则需要重写loadClass&#xff0c;一个findClass必须要重新&#xff0c;因为父类是空的&#xff0c;…
阅读更多...
SpringBoot3之GraalVM之Linux详细安装及使用教程

SpringBoot3之GraalVM之Linux详细安装及使用教程

Linux安装底层工具相关依赖 yum install -y gcc glibc-devel zlib-devel安装GraalVM JDK 《GraalVM官网下载》 找到最近的GraalVM Community Edition X.X.X点击Assets&#xff08;因为我的是SpringBoot3项目&#xff0c;起始JDK就要求17&#xff0c;所以我下载17&#xff09;下…
阅读更多...
青少年机器人技术一级核心知识点：机械结构及模型（一）

青少年机器人技术一级核心知识点：机械结构及模型（一）

随着科技的不断进步&#xff0c;机器人技术已经成为了一个重要的领域。在这个领域中&#xff0c;机械结构是机器人设计中至关重要的一部分&#xff0c;它决定了机器人的形态、运动方式和工作效率。对于青少年机器人爱好者来说&#xff0c;了解机械结构的基础知识&#xff0c;掌…
阅读更多...
vim背景颜色设置

vim背景颜色设置

cd ~进入个人家目录下&#xff0c;vim .vimrc进入vimrc文件&#xff1a; 在主题设置部分对颜色背景进行设置&#xff0c;onedark表示黑色背景&#xff0c;default表示白色背景&#xff0c;按需设置即可&#xff01;
阅读更多...
网络知识点-链路聚合

网络知识点-链路聚合

链路聚合&#xff08;英语&#xff1a;Link Aggregation&#xff09;是一个计算机网络术语&#xff0c;指将多个物理端口汇聚在一起&#xff0c;形成一个逻辑端口&#xff0c;以实现出/入流量吞吐量在各成员端口的负荷分担&#xff0c;交换机根据用户配置的端口负荷分担策略决定…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023