import random
import matplotlib.pyplot as plt

plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题


# 创建初始种群
def create_initial_population():
    population = []
    for _ in range(population_size):
        chromosome = list(cities.keys())
        random.shuffle(chromosome)
        population.append(chromosome)
    return population


# 计算两个城市之间的距离
def distance(city1, city2):
    x1, y1 = cities[city1]
    x2, y2 = cities[city2]
    return ((x1 - x2) ** 2 + (y1 - y2) ** 2) ** 0.5


# 计算适应度（路径长度）
def calculate_fitness(chromosome):
    total_distance = 0
    for i in range(len(chromosome) - 1):
        city1, city2 = chromosome[i], chromosome[i + 1]
        total_distance += distance(city1, city2)
    return total_distance


# 选择精英个体
def select_elite(population):
    elite = []
    sorted_population = sorted(population, key=lambda chromosome: calculate_fitness(chromosome))
    for i in range(elite_size):
        elite.append(sorted_population[i])
    return elite


# 进化过程（交叉和变异）
def evolve_population(population):
    # 选择精英种群
    elite = select_elite(population)
    new_population = elite.copy()
    # 初始种群数量， population_size = 50
    while len(new_population) < population_size:
        parent1 = random.choice(elite)
        parent2 = random.choice(elite)
        # 交叉操作
        child = crossover(parent1, parent2)
        mutate(child)
        # 交叉操作后的种群添加到新的种群里面去
        new_population.append(child)
    # 返回新的种群
    return new_population


# 交叉操作
def crossover(parent1, parent2):
    child = ['-'] * len(parent1)
    start = random.randint(0, len(parent1) - 1)
    end = random.randint(start, len(parent1) - 1)
    child[start:end+1] = parent1[start:end+1]
    for city in parent2:
        if city not in child:
            index = child.index('-')
            child[index] = city
    return child


# 变异操作
def mutate(chromosome):
    for i in range(len(chromosome)):
        if random.random() < mutation_rate:
            j = random.randint(0, len(chromosome) - 1)
            # 染色体的两个片段进行交互
            chromosome[i], chromosome[j] = chromosome[j], chromosome[i]


# 主函数
def run():
    # 创建初始种群, 随机生成n个种群
    population = create_initial_population()
    best_distance = float('inf')
    best_chromosome = []

    # 进化一百次
    for _ in range(generations):
        # 把随机生成的种群放进去进化
        population = evolve_population(population)
        # 计算当前的适应度，并选出最小的（路径）的一组
        current_best = min(population, key=lambda chromosome: calculate_fitness(chromosome))
        current_distance = calculate_fitness(current_best)
        # 比较当前的最小距离和全局最优的距离
        if current_distance < best_distance:
            best_distance = current_distance
            best_chromosome = current_best

    print("最短路径：", best_chromosome)
    print("最短路径长度：", best_distance)
    return best_chromosome


# 运行主函数
if __name__ == "__main__":
    # 城市坐标
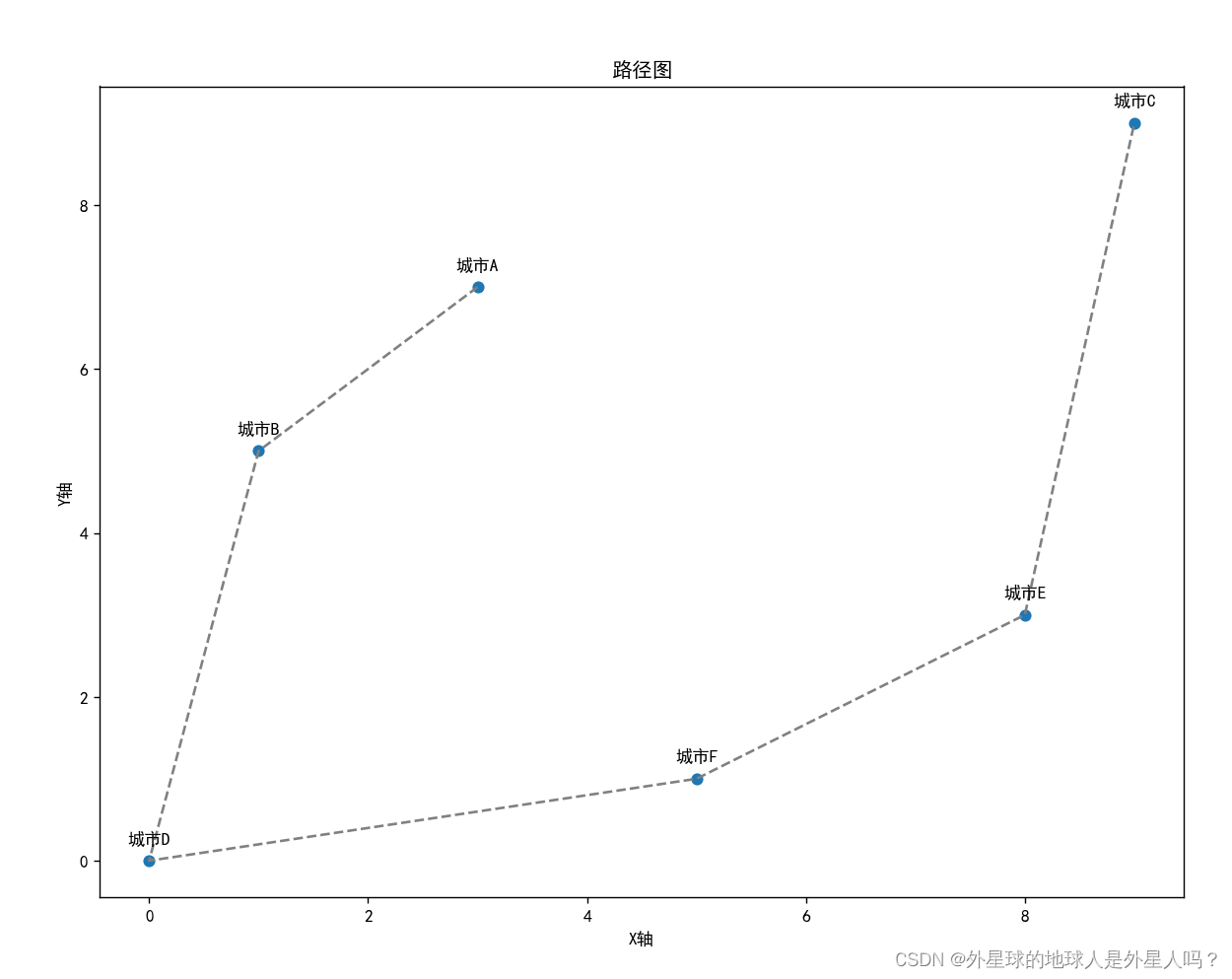
    cities = {
        '城市A': (3, 7),
        '城市B': (1, 5),
        '城市C': (9, 9),
        '城市D': (0, 0),
        '城市E': (8, 3),
        '城市F': (5, 1)
    }

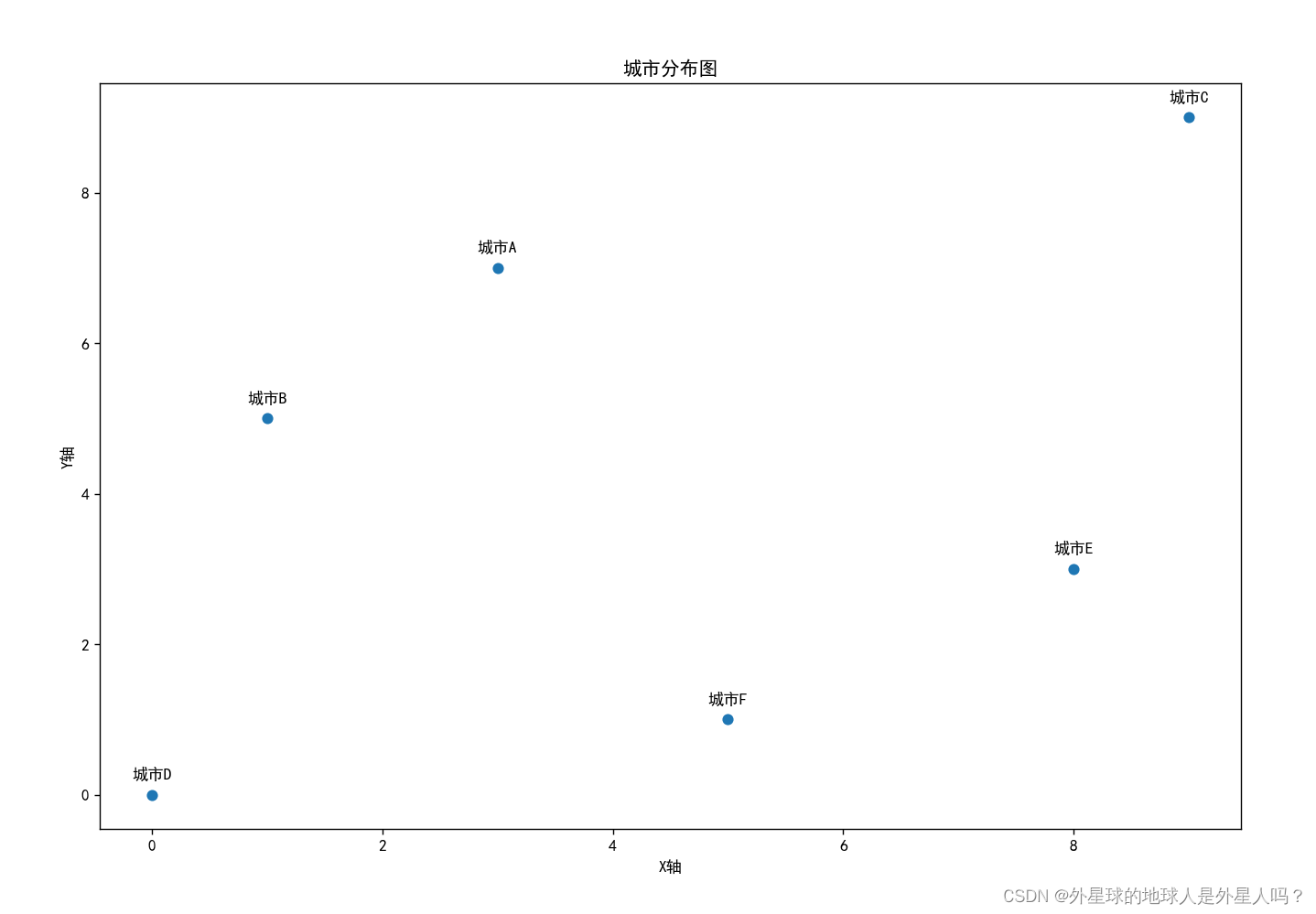
    x = [cities[k][0] for k in cities]
    y = [cities[k][1] for k in cities]
    fig, ax = plt.subplots()
    scatter = ax.scatter(x, y)
    ax.set_xlabel('X轴')
    ax.set_ylabel('Y轴')
    ax.set_title('城市分布图')
    for i, txt in enumerate(cities.keys()):
        ax.annotate(txt, (x[i], y[i]), textcoords='offset points', xytext=(0, 10), ha='center')
    # 显示图形
    plt.show()

    # 遗传算法参数
    # 初始种群数量
    population_size = 50
    # 精英个体数量，即每次进化，筛选出来的数量
    elite_size = 10
    # mutation_rate（变异率），表示在交叉操作后发生基因变异的概率
    mutation_rate = 0.01
    # 进化次数
    generations = 100
    res = run()

    res_x = [cities[r][0] for r in res]
    res_y = [cities[r][1] for r in res]
    fig, ax = plt.subplots()
    scatter = ax.scatter(res_x, res_y)
    path = ax.plot(res_x, res_y, '--', color='gray')
    ax.set_xlabel('X轴')
    ax.set_ylabel('Y轴')
    ax.set_title('路径图')
    for i, txt in enumerate(res):
        ax.annotate(txt, (res_x[i], res_y[i]), textcoords='offset points', xytext=(0, 10), ha='center')
    plt.show()