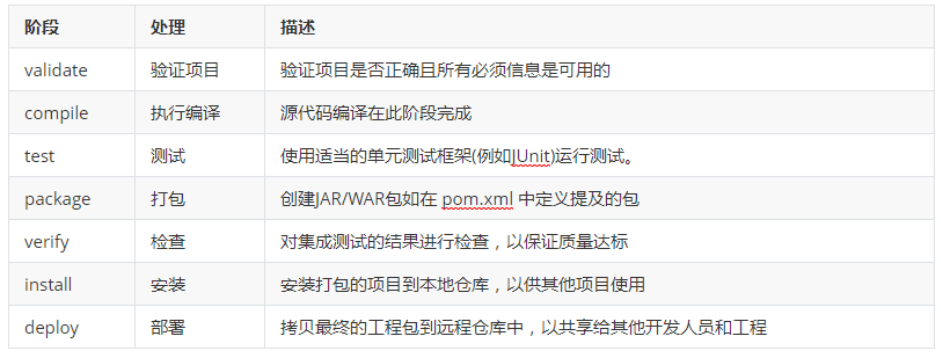
目录
- DL基础
- 前言
- 1. BP训练mnist
- 2. 权重初始化理论分析
- 总结
DL基础
前言
手写AI推出的全新保姆级从零手写自动驾驶CV课程,链接。记录下个人学习笔记,仅供自己参考。
本次课程我们来了解下 BP 反向传播和学习权重初始化相关知识
课程大纲可看下面的思维导图。

1. BP训练mnist
BP(back propagation)误差反向传播算法是当前人工智能主要采用的算法,如 CNN、GAN、Transformer 等都是 BP 体系下的算法框架,这节课我们从一个不同的角度来了解下 BP
我们先来回顾下之前学习到的知识
对于给定房屋面积预测房价的任务,属于单个变量和单个输出的模型,其对应表达如下:
y
=
k
x
+
b
y = kx + b
y=kx+b
对于给定房屋面积、距离地铁远近、装修程度预测房价的任务,属于多个变量和单个输出的模型,其对应表达如下:
y
=
k
1
x
1
+
k
2
x
2
+
k
3
x
3
+
b
y = k_1x_1+k_2x_2+k_3x_3+b
y=k1x1+k2x2+k3x3+b
对于给定房屋面积、距离地铁远近、装修程度预测房价和租金的任务,属于多个变量和多个输出的模型(多模型),其对应表达如下:
y
1
=
k
1
x
1
+
k
2
x
2
+
k
3
x
3
+
b
1
y
2
=
p
1
x
1
+
p
2
x
2
+
p
3
x
3
+
b
2
y_1 = k_1x_1 + k_2x_2 + k_3x_3 + b_1 \\ y_2 = p_1x_1 + p_2x_2 + p_3x_3 + b_2
y1=k1x1+k2x2+k3x3+b1y2=p1x1+p2x2+p3x3+b2
而我们今天要学习的 BP 可以看作是多模型的堆叠,将中间的表示抽象出来,我们以一次抽象为例来讲解,实际可以进行多次抽象,看作是多个层次的堆叠
中间的抽象层可以定义为:
h
1
=
k
1
x
1
+
k
2
x
2
+
k
3
x
3
+
b
1
h
2
=
p
1
x
1
+
p
2
x
2
+
p
3
x
3
+
b
2
h_1 = k_1x_1 + k_2x_2 + k_3x_3 + b_1 \\ h_2 = p_1x_1 + p_2x_2 + p_3x_3 + b_2
h1=k1x1+k2x2+k3x3+b1h2=p1x1+p2x2+p3x3+b2
我们往往不只是做简单的堆叠,因为这样堆叠出来的模型没有非线性的特性,表达能力偏弱,因此,我们会在中间层之后额外加一个非线性的表达,增强模型的表达能力。
h
1
=
f
u
n
c
(
h
1
)
h
2
=
f
u
n
c
(
h
2
)
h_1 = func(h_1) \\ h_2 = func(h_2)
h1=func(h1)h2=func(h2)
最后我们再得到我们想要的目标结果
y
1
=
m
1
h
1
+
m
2
h
2
+
b
3
y
2
=
n
1
h
1
+
n
2
h
2
+
b
4
\begin{aligned} y_1 &= m_1h_1 + m_2h_2 + b3 \\ y_2 &= n_1h_1 + n_2h_2 + b4 \end{aligned}
y1y2=m1h1+m2h2+b3=n1h1+n2h2+b4
OK!经过上述分析之后,我们再来看具体的代码实现
我们只需要将上节课中的多分类逻辑回归的示例代码略微修改即可
我们需要加一层隐藏层,假设隐藏层的输出数量为 256, k k k 和 b b b 的定义如下:
# 定义k和b
hidden_size = 256
num_classes = 10
k1 = np.random.randn(784, hidden_size)
b1 = np.zeros((1, hidden_size))
k2 = np.random.randn(hidden_size, num_classes)
b2 = np.zeros((1, num_classes))
模型预测时也需要发生一些变化,输入先经过 k 1 k_1 k1 和 b 1 b_1 b1 得到隐藏层的输出,随后经过非线性激活函数 relu,最后经过 k 2 k_2 k2 和 b 2 b_2 b2 得到最终的预测输出。由于多了一层,因此 loss 的求导也发生了对应的变化,但是原理还是一样,示例代码如下:
def relu(x):
x = x.copy()
x[x < 0] = 0
return x
def drelu(x, G):
G = G.copy()
G[x < 0] = 0
return G
for epoch in range(10):
for images, labels in train_loader:
niter += 1
# 32x784 @ 784x256
hidden = images @ k1 + b1
# nonlinear
nonlinear_hidden = relu(hidden)
# predict
predict = nonlinear_hidden @ k2 + b2
# predict -> logits
logits = softmax(predict, dim=1)
# softmax crossentropy loss
# loss = -(y * ln(p))
batch = logits.shape[0]
onehot_labels = np.zeros_like(logits)
# labels(32,) -> onehot(32,10)
onehot_labels[np.arange(batch), labels] = 1
loss = crossentropy_loss(logits, onehot_labels)
if niter % 100 == 0:
print(f"Epoch: {epoch}, Iter: {niter}, Loss: {loss:.3f}")
G = (logits - onehot_labels) / batch
# C = AB
# dA = G @ B.T
# dB = A.T @ G
delta_k2 = nonlinear_hidden.T @ G
delta_b2 = G.sum(axis=0, keepdims=True)
delta_nonlinear_hidden = G @ k2.T
delta_hidden = drelu(hidden, delta_nonlinear_hidden)
delta_k1 = images.T @ delta_hidden
delta_b1 = delta_hidden.sum(axis=0, keepdims=True)
k1 = k1 - lr * delta_k1
b1 = b1 - lr * delta_b1
k2 = k2 - lr * delta_k2
b2 = b2 - lr * delta_b2
验证部分也需要相应的修改,代码如下:
# evaluate
all_predict = []
for images, labels in test_loader:
hidden = images @ k1 + b1
# nonlinear
nonlinear_hidden = relu(hidden)
predict = nonlinear_hidden @ k2 + b2
logits = softmax(predict, dim=1)
predict_labels = logits.argmax(axis=1)
all_predict.extend(predict_labels == labels)
accuracy = np.sum(all_predict) / len(all_predict) * 100
print(f"Epoch: {epoch}, Evaluate Test Set, Accuracy: {accuracy:.3f} %")
运行效果如下:

可以看到 loss 直接飞了,这是因为 k k k 采用正态分布的初始化,其值比较大,当计算 loss 时 ln 直接跑飞了,因此,我们可以将 k 1 k_1 k1 和 k 2 k_2 k2 缩小,在下次课程中我们会对权重的初始化进行详细的分析,具体代码如下:
k1 = np.random.randn(784, hidden_size) * 0.1
b1 = np.zeros((1, hidden_size))
k2 = np.random.randn(hidden_size, num_classes) * 0.1
b2 = np.zeros((1, num_classes))
修改后运行的效果如下:

可以看到此时的 loss 输出值正常,且第一个 epoch 准确率就达到了 92.93%,效果还是不错的。
接下来我们可以将模型预测的结果进行简单的可视化,代码如下:
for images, labels in test_loader:
hidden = images @ k1 + b1
nonlinear_hidden = relu(hidden)
predict = nonlinear_hidden @ k2 + b2
logits = softmax(predict, dim=1)
predict_labels = logits.argmax(axis=1)
pixels = (images * train_dataset.std + train_dataset.mean).astype(np.uint8).reshape(-1, 28, 28)
for image, predict, gt in zip(pixels, predict_labels, labels):
plt.imshow(image)
plt.title(f"Predict: {predict}, GT: {gt}")
plt.show()
可视化的部分结果如下所示:


可以看到模型预测的结果还是比较准确的。
对于 BP 反向传播算法的不同理解可以参考 彻底理解BP反向传播,BP实战图像分类98.3%
完整的示例代码如下所示:
import numpy as np
import matplotlib.pyplot as plt
class MNISTDataset:
def __init__(self, images_path, labels_path, train, mean=None, std=None):
self.images_path = images_path
self.labels_path = labels_path
self.images, self.labels = self.load_mnist_data()
# flatten Nx28x28 -> Nx784
self.images = self.images.reshape(len(self.images), -1)
if train:
self.images, self.mean, self.std = self.normalize(self.images)
else:
self.images, self.mean, self.std = self.normalize(self.images, mean, std)
@staticmethod
def normalize(x, mean=None, std=None):
if mean is None:
mean = x.mean()
if std is None:
std = x.std()
x = (x - mean) / std
return x, mean, std
def __len__(self):
return len(self.images)
def __getitem__(self, index):
image, label = self.images[index], self.labels[index]
return image, label
def load_mnist_data(self):
# load labels
with open(self.labels_path, "rb") as f:
magic_number, num_of_items = np.frombuffer(f.read(8), dtype=">i", count=2, offset=0)
labels = np.frombuffer(f.read(), dtype=np.uint8, count=-1, offset=0)
# load images
with open(self.images_path, "rb") as f:
magic_number, num_of_images, rows, cols = np.frombuffer(f.read(16), dtype=">i", count=4, offset=0)
pixels = np.frombuffer(f.read(), dtype=np.uint8, count=-1, offset=0)
images_matrix = pixels.reshape(num_of_images, rows, cols)
return images_matrix, labels
class MNISTDataLoader:
def __init__(self, dataset, batch_size, shuffle=True):
self.dataset = dataset
self.batch_size = batch_size
self.shuffle = shuffle
def __iter__(self):
self.indexs = np.arange(len(self.dataset))
if self.shuffle:
np.random.shuffle(self.indexs)
self.cursor = 0
return self
def __next__(self):
begin = self.cursor
end = self.cursor + self.batch_size
if end > len(self.dataset):
raise StopIteration()
self.cursor = end
batched_data = []
for index in self.indexs[begin:end]:
item = self.dataset[index]
batched_data.append(item)
# return batched_data
return [np.stack(item, axis=0) for item in list(zip(*batched_data))]
# 训练集
train_dataset = MNISTDataset("mnist/train-images-idx3-ubyte", "mnist/train-labels-idx1-ubyte", train=True)
train_loader = MNISTDataLoader(train_dataset, batch_size=32, shuffle=True)
# 测试集
test_dataset = MNISTDataset(
"mnist/t10k-images-idx3-ubyte",
"mnist/t10k-labels-idx1-ubyte",
train=False,
mean=train_dataset.mean,
std=train_dataset.std
)
test_loader = MNISTDataLoader(test_dataset, 10)
# 定义k和b
hidden_size = 256
num_classes = 10
k1 = np.random.randn(784, hidden_size) * 0.1
b1 = np.zeros((1, hidden_size))
k2 = np.random.randn(hidden_size, num_classes) * 0.1
b2 = np.zeros((1, num_classes))
def relu(x):
x = x.copy()
x[x < 0] = 0
return x
def drelu(x, G):
G = G.copy()
G[x < 0] = 0
return G
def softmax(x, dim):
x = np.exp(x - x.max())
return x / x.sum(axis=dim, keepdims=True)
def crossentropy_loss(logits, onehot_labels):
batch = logits.shape[0]
return -(onehot_labels * np.log(logits)).sum() / batch
lr = 1e-2
niter = 0
for epoch in range(1):
for images, labels in train_loader:
niter += 1
# 32x784 @ 784x256
hidden = images @ k1 + b1
# nonlinear
nonlinear_hidden = relu(hidden)
# predict
predict = nonlinear_hidden @ k2 + b2
# predict -> logits
logits = softmax(predict, dim=1)
# softmax crossentropy loss
# loss = -(y * ln(p))
batch = logits.shape[0]
onehot_labels = np.zeros_like(logits)
# labels(32,) -> onehot(32,10)
onehot_labels[np.arange(batch), labels] = 1
loss = crossentropy_loss(logits, onehot_labels)
if niter % 100 == 0:
print(f"Epoch: {epoch}, Iter: {niter}, Loss: {loss:.3f}")
G = (logits - onehot_labels) / batch
# C = AB
# dA = G @ B.T
# dB = A.T @ G
delta_k2 = nonlinear_hidden.T @ G
delta_b2 = G.sum(axis=0, keepdims=True)
# dloss / dhidden
delta_nonlinear_hidden = G @ k2.T
delta_hidden = drelu(hidden, delta_nonlinear_hidden)
delta_k1 = images.T @ delta_hidden
delta_b1 = delta_hidden.sum(axis=0, keepdims=True)
k1 = k1 - lr * delta_k1
b1 = b1 - lr * delta_b1
k2 = k2 - lr * delta_k2
b2 = b2 - lr * delta_b2
# evaluate
all_predict = []
for images, labels in test_loader:
hidden = images @ k1 + b1
# nonlinear
nonlinear_hidden = relu(hidden)
predict = nonlinear_hidden @ k2 + b2
logits = softmax(predict, dim=1)
predict_labels = logits.argmax(axis=1)
all_predict.extend(predict_labels == labels)
accuracy = np.sum(all_predict) / len(all_predict) * 100
print(f"Epoch: {epoch}, Evaluate Test Set, Accuracy: {accuracy:.3f} %")
for images, labels in test_loader:
hidden = images @ k1 + b1
nonlinear_hidden = relu(hidden)
predict = nonlinear_hidden @ k2 + b2
logits = softmax(predict, dim=1)
predict_labels = logits.argmax(axis=1)
pixels = (images * train_dataset.std + train_dataset.mean).astype(np.uint8).reshape(-1, 28, 28)
for image, predict, gt in zip(pixels, predict_labels, labels):
plt.imshow(image)
plt.title(f"Predict: {predict}, GT: {gt}")
plt.show()
2. 权重初始化理论分析
我们先来对上节课 BP 训练 mnist 做一个回顾,在上节课中我们发现直接采用正态分布的随机数来初始权重 k k k 会导致最终的 loss 直接跑飞,因此我们将其值乘了 0.1 进行缩小,发现缩小后的初始化权重 k k k 能达到一个比较好的结果。
为什么一定要使用正态分布的随机数来对权重进行初始化呢?使用其他分布可以吗?🤔
下面我们对比了采用均匀分布随机数和正态分布随机数来初始化权重 k k k 的损失和模型的性能
rand -> loss: 2.127, accuracy: 87.010%
randn -> loss: 0.365, accuracy: 93.100%
可以看到二者差别还是比较大的,均匀分布的随机数初始化的 loss 要高,且准确率也偏低。这说明不同的权重初始化方法会影响最终的模型性能,为什么正态分布的随机数初始化会比均匀分布的随机数初始化效果要好呢?这就是我们接下来要讨论的问题。
我们可以回想下之前求取 2 \sqrt 2 2 的例子中,我们将 t t t 初始化为 x / 2 x/2 x/2,因为这个数更能够接近目标值一些,所以它的开始 loss 会更低,迭代次数也会更少。
现在考虑线性回归模型
y
=
k
x
+
b
y = kx + b
y=kx+b
问题:如何定义
k
k
k 和
b
b
b,在理论上认为是相对比较好的初始点?
我们需要分析 y = k x + b y = kx + b y=kx+b 这个函数以及所有变量的性质,下面我们一个个分析
x x x:输入的数据
- x x x 通常来自于统计得到的数据,来自于日常生活中产生的数据。我们可以通过数据产生的概率来描述它,我们认为 x x x 通常会满足极端数据少,平均数据多的情况
- 既然 x x x 符合我们日常生活中的数据,那不妨我们使用正态分布来描述 x x x,这其实是对日常收集到的数据的一个假设,因为日常生活中的很多数据比如一个班级的成绩、身高、体重等都是符合正态分布的,因此,对 x x x 做正态分布假设是一个非常具有通用型的设计
- 在之前的实现中,我们通常会对
x
x
x 做正则化,即
x -> normalize(x), (x - mean) / std,它其实是把 x x x 正则化到一个标准的正态分布下。因此最终的 x ∼ N ( 0 , 1 ) x\sim N\left(0,1\right) x∼N(0,1)
y y y:输出的值
- y y y 是对于输入数据 x x x 的映射后的一个值,我们从统计的角度来看, y y y 依旧是随着 x x x 而言的,依旧是正态分布
y -> normalize(y), (y - mean) / std, y ∼ N ( 0 , 1 ) y\sim N\left(0,1\right) y∼N(0,1)
因此我们可以得出结论,对于 k k k 和 b b b 的设计而言,如果能够使得 x x x 经过 k k k 和 b b b 过后的分布不产生变化,那么 k k k 和 b b b 将会是一个比较好的初始化位置。
具体我们该如何设计 k k k 和 b b b 的初始值使得分布不会产生变化呢?
在开始之前我们需要对 np.random.randn 有一个简单的了解
import numpy as np
x = np.random.randn(784, 256)
# mean -> 均值
# std -> 标准差
# var -> 方差
# 其中 var = std^2
print(x.mean(), x.std(), x.var())
如果对服从正态分布的变量乘以某个常数或者加上某个常数后的分布又是怎样的呢?
那这就不得不提关于正态分布的一些特性了
- 如果 X ∼ N ( μ , σ 2 ) X\sim N\left(\mu,{\sigma}^2\right) X∼N(μ,σ2) 且 a a a 是实数,那么 a X ∼ N ( a μ , ( a σ ) 2 ) aX \sim N\left(a\mu,(a\sigma)^2\right) aX∼N(aμ,(aσ)2)
- 如果 X ∼ N ( μ , σ 2 ) X\sim N\left(\mu,{\sigma}^2\right) X∼N(μ,σ2) 且 b b b 是实数,那么 X + b ∼ N ( μ + b , σ 2 ) X+b \sim N\left(\mu+b,{\sigma}^2\right) X+b∼N(μ+b,σ2)
- 更多细节可参考 wiki
根据正态分布的上面两条特性我们可以完成对 k k k 和 b b b 的初始值的设计了
首先 predict = x @ k + b,我们需要确保输入 predict 的分布与 x 保持一致都为标准正态分布。当输入 x 乘以 k 后其标准差为发生变化,我们目的当然是希望它不发生变化,乘完之后还是和 x 保持一致
我们先来看一个简单的例子:
x = np.random.randn(784, 256)
k = np.random.randn(256, 64)
predict = x @ k
# 0.04331550600632987 16.002218532647994 256.0709979666229
print(predict.mean(), predict.std(), predict.var())
可以看到二者相乘后依旧服从正态分布,其均值依旧是 0,而标准差则为 256 = 16 \sqrt {256} = 16 256=16
为什么结果矩阵会服从均值为 0,标准差为 16 的正态分布呢?以下是 chatGPT 给出的解释
首先,对于标准正态分布的随机变量 x x x 和 k k k,它们的均值为 0,标准差为 1
当 x x x 和 k k k 相乘后,得到一个新的矩阵 m m m 其维度为 (784,64)。 m m m 中的每个元素 m ( i , j ) m (i,j) m(i,j) 是由 x x x 的第 i i i 行与 k k k 的第 j j j 列进行内积运算得到的
由于 x x x 和 k k k 都服从标准正态分布,它们的每个维度都是独立的随机变量。在独立随机变量相乘的情况下,我们可以应用卷积和中心极限定理。
根据卷积和中心极限定理的原理,当进行大量独立随机变量的相乘时,结果的分布会趋近于正态分布。
在当前的情况下, m m m 中的每个元素都是由 256 个独立的随机变量相乘得到的,而这些随机变量都来自于标准正态分布,根据中心极限定理,这样的相乘操作会导致结果的分布趋近于正态分布。因此, m m m 的元素也会服从正态分布
对于均值的推导,由于 x x x 和 k k k 的均值为 0,它们的内积的期望值也为 0。因此, m m m 的每个元素的期望值为 0,即 m m m 的均值为 0
对于标准差的推导,由于每个 x x x 和 k k k 的元素独立的且标准差均为 1,内积的标准差会变为相乘元素个数的平方根。在当前情况下, x x x 和 k k k 的维度均为 256,所以相乘后的标准差为 256 \sqrt {256} 256,即 16。
一切似乎变得清晰明了了呀😄,简单来说 m m m 中的每个元素都是由 256 个独立的随机变量相乘得到。而这些随机变量来自于标准正态分布
假设
X
X
X 和
Y
Y
Y 服从标准正态分布且独立,现在需要计算它们的乘积
Z
=
X
Y
Z = XY
Z=XY 的均值和标准差
E
(
Z
)
=
E
(
X
Y
)
=
E
(
X
)
E
(
Y
)
=
0
V
a
r
(
Z
)
=
V
a
r
(
X
Y
)
=
E
[
(
X
Y
−
E
[
X
Y
]
)
2
]
=
E
[
(
X
Y
)
2
]
=
E
[
X
2
Y
2
]
=
E
(
X
2
)
E
(
Y
2
)
=
V
a
r
(
X
)
V
a
r
(
Y
)
=
1
\begin{aligned} E(Z) &=E(XY)=E(X)E(Y)=0 \\ Var(Z) &=Var(XY)=E[(XY - E[XY])^2] \\ &=E[(XY)^2]=E[X^2Y^2] \\ &=E(X^2)E(Y^2) \\ &= Var(X)Var(Y) \\ &= 1 \end{aligned}
E(Z)Var(Z)=E(XY)=E(X)E(Y)=0=Var(XY)=E[(XY−E[XY])2]=E[(XY)2]=E[X2Y2]=E(X2)E(Y2)=Var(X)Var(Y)=1
因此 256 个独立的均值为 0,方差为 1 的随机变量相加后的均值为 0,方差为 256,标准差为 16
根据正态分布的第一条特性,要想让其标准差变为 1,只需要除以 16 即可
D = 256
x = np.random.randn(784, D)
k = np.random.randn(D, 64)
predict = x @ k
predict = predict / np.sqrt(D)
# 0.0029998421515664217 0.993879430767524 0.9877963229027776
print(predict.mean(), predict.std(), predict.var())
可以看到结果符合我们的预期,那么关于 k k k 的设计我们就清楚了
k
k
k 的设计:
k
∼
N
(
0
,
1
D
)
k \sim N(0, \frac{1}{\sqrt D})
k∼N(0,D1) 其中 D = k.rows
接下来我们看下
b
b
b 的设计,根据正态分布特性第二条,当加上一个随机数时其均值会发生变化,而方差不变,为了让最终的 predict 和 x 的分布保持一致,我们需要将这个均值去除,很简单,我们将
b
b
b 设置为 0 即可。
b b b 的设计:0
当
k
k
k 和
b
b
b 的设计符合上述条件时,predict = x @ k + b 就会实现
x
x
x 经过
k
k
k 和
b
b
b 后的分布不产生变化,满足我们的要求。
对于线性回归模型的权重初始化比较简单,而对于 BP 神经网络来说可能稍微复杂点
h = x @ k1 + b1
ha = nonlinear(h)
predict = ha @ k2 + b2
对于模型的参数设计而言,我们依旧希望 x x x 经过 k 1 k_1 k1 b 1 b_1 b1 n o n l i n e a r nonlinear nonlinear k 2 k_2 k2 b 2 b_2 b2 后,得到的 p r e d i c t predict predict 保持分布不变
由于 n o n l i n e a r nonlinear nonlinear 会改变分布的性质,因此在对 k 1 k_1 k1 b 1 b_1 b1 k 2 k_2 k2 b 2 b_2 b2 做初始化时需要将其考虑进去
对于 n o n l i n e a r nonlinear nonlinear 的权重初始化我们可以采用凯明初始化
凯明初始化
fan_in,fan_out
fan_in -> k.rows fan_out -> k.cols
mean = 0
std = gain / sqrt(fan_in + fan_out)
关于不同的非线性函数对应的增益可参考 pytorch 官网 torch.nn.init,非线性函数不同对应的增益也将不同,比如 ReLU 的增益为 2 \sqrt 2 2
关于凯明初始化的更多细节需要大家自行补充
-
Xavier 初始化 Paper:Understanding the difficulty of training deep feedforward neural networks
-
Kaiming 初始化 Paper:Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
-
几种常见的权重初始化方法
-
一文搞懂深度网络初始化(Xavier and Kaiming initialization)
总结
本次课程从一个新奇的角度带我们了解了 BP 算法,我们可以将其理解为多模型的堆叠,将中间的隐藏层抽象出来,可以不断的叠加,也比较符合人类社会的阶级制度。但值得注意的是我们往往会将中间隐藏层的输出经过一个非线性变换,在本次课程中我们是使用 relu 函数来实现的,这样可以加强模型的非线性表达能力,增强模型的性能。
本次课程还学习了权重初始化的相关理论知识,我们从线性回归模型出发最终得出了 k k k 和 b b b 的设计,二者的设计思路是确保 x x x 经过 k k k 和 b b b 后其分布不发生变化。根据这个设计思路我们可以推广到 BP 神经网络中权重的设计,由此引出了 Kaming 初始化,其均值为 0,方差为 gain/(fan_in+fan_out),不同激活函数对应的增益也不尽相同。