哈喽，大家好，我是雷工！
今天测试KingIOServer连接ModbusTCP设备，下面记录测试过程。

一、ModbusTCP设备

利用ModbusSlave模拟Modbus从站设备。
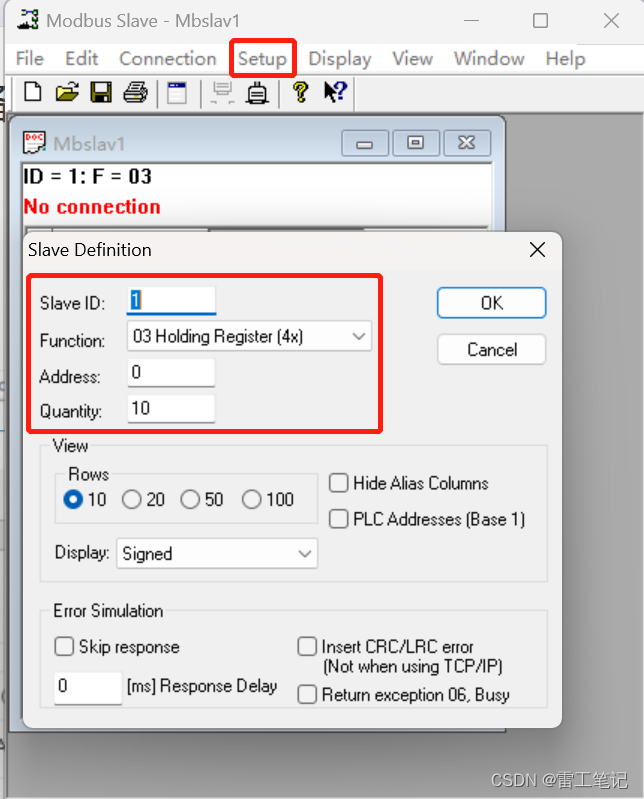
1、打开ModbusSlave软件，点击菜单栏【Setup】—>【SlaveDefinition…】

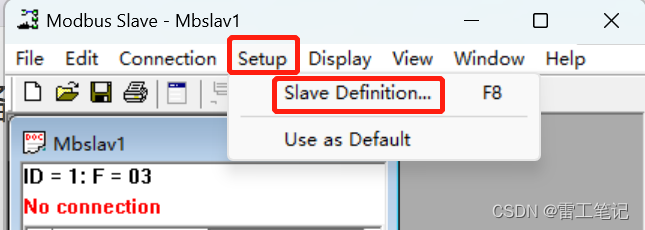
2、设置相关参数。
Slave ID :设置从站地址；
Function:设置功能码；
Address:设置寄存器地址；
Quantity:设置寄存器数量；

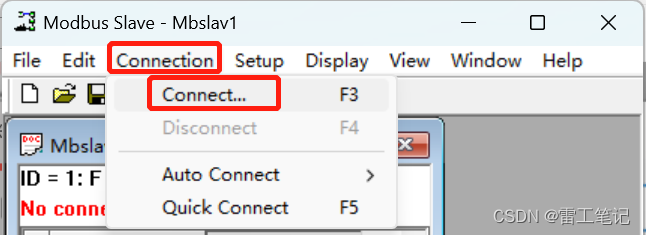
3、点击菜单栏【Connection】—>【connect…】。

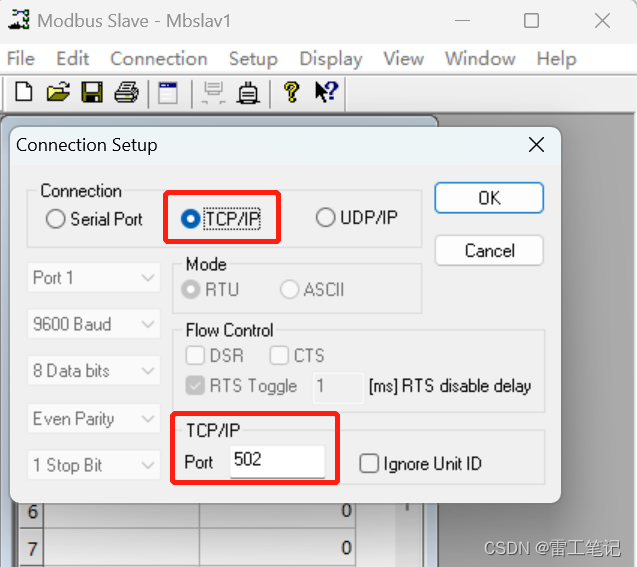
4、Connection Setup
Connection选择【TCP/IP】;
TCP/IP Port:设置端口；

二、KingIOServer配置

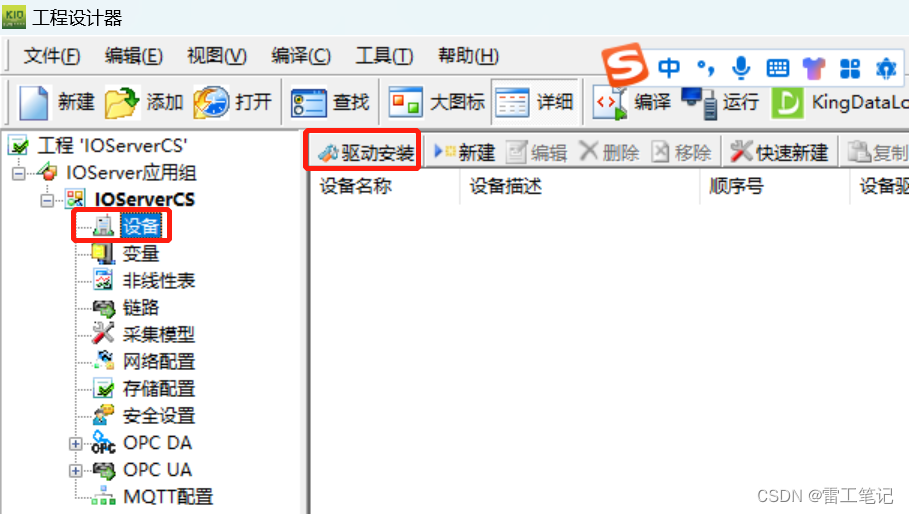
1、新建IOServer项目后，点击【设备】，选择【驱动安装】，安装上ModbusTCP驱动。

2、新建设备，设置设备名称，设备系列，种类等参数；

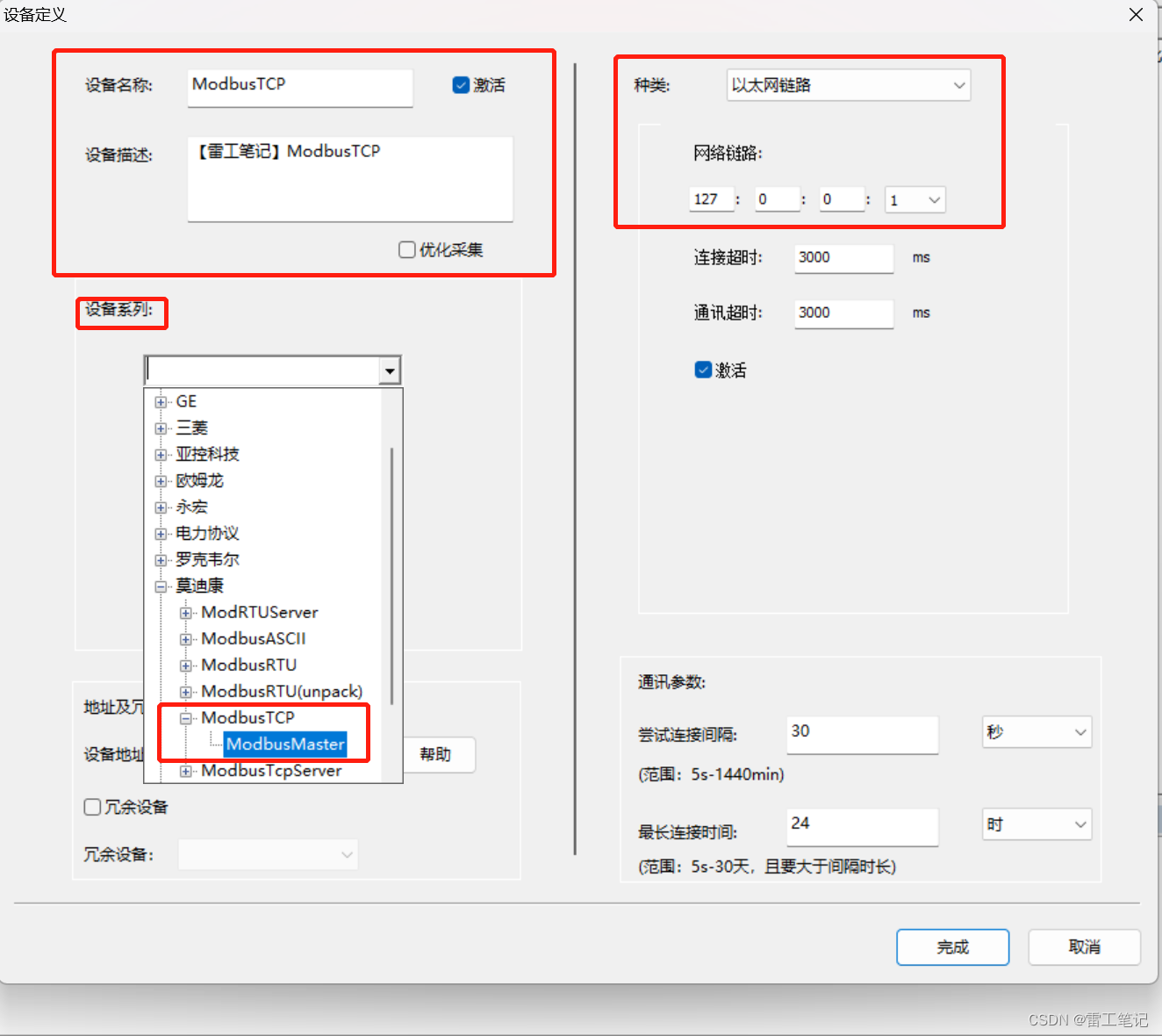
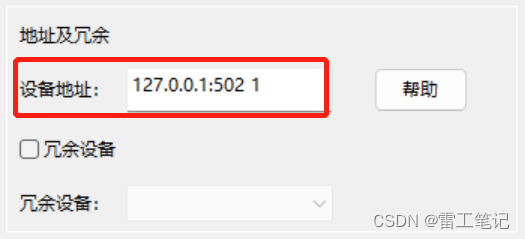
3、设置设备地址，然后点击确定。

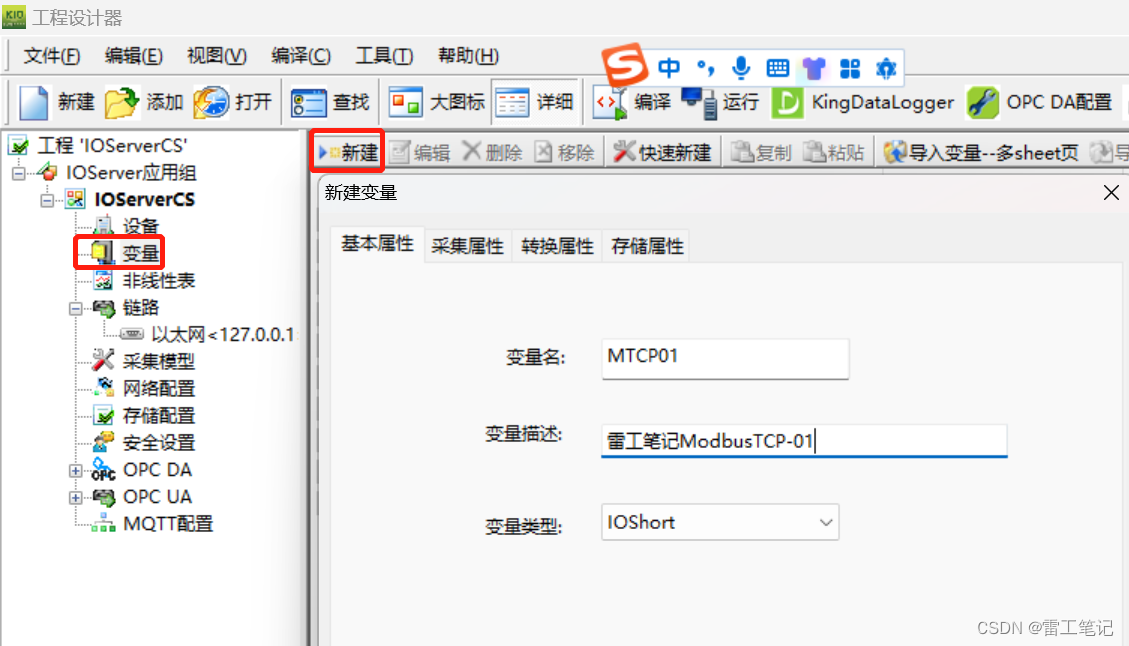
4、新建变量：设置基本属性。

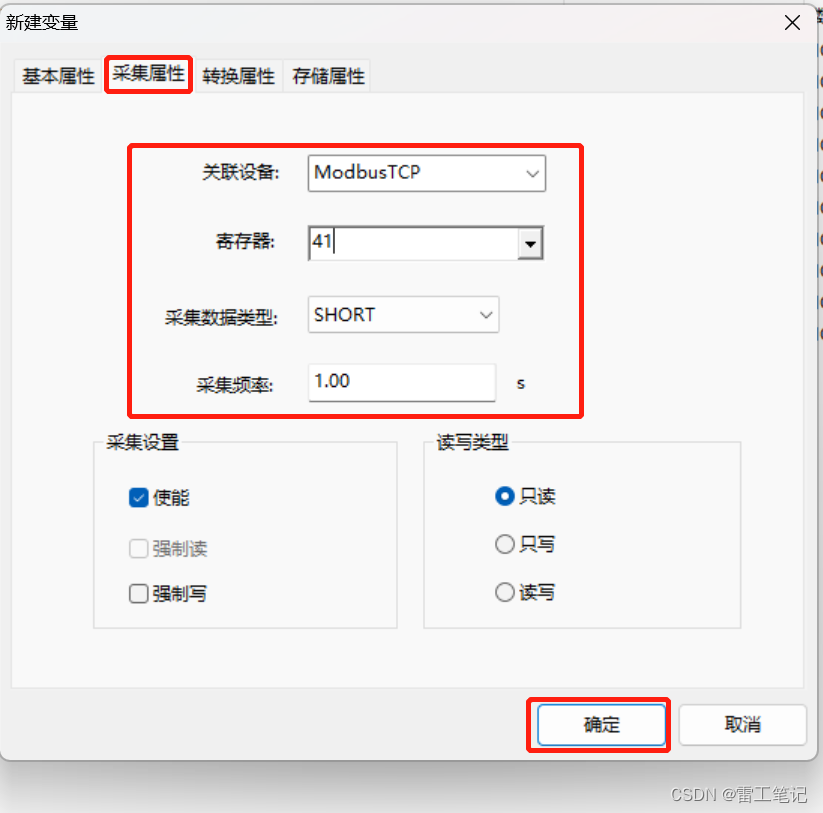
5、设置采集属性，然后点击确定。

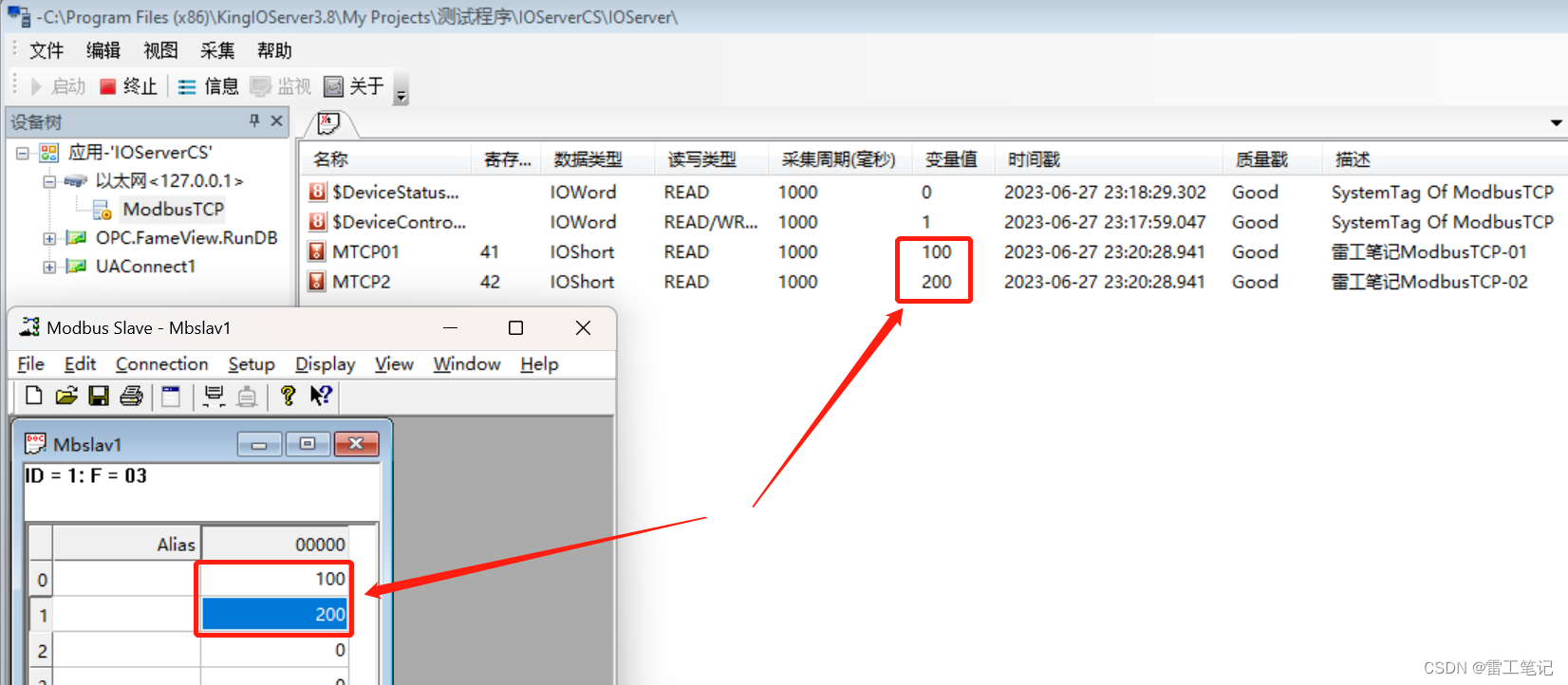
6、然后点击运行，查看结果值，显示结果与ModbusSlave设置的值一致，说明通讯正常。

后记

以上为简单的通讯测试，具体其他数据类型，或处理方式等可根据现场实际情况进行调整测试，对比与采集值一致说明采集配置正常。