文章目录
- 前言
- 课前温习
- 一、快速排序
- 核心模板
- 1.1题目描述
- 1.2思路分析
- 1.3代码实现
- 二、归并排序
- 核心模板
- 2.1题目描述
- 2.2思路分析
- 2.3代码实现
- 三、二分查找
- 整数二分
- 题目一
- 3.1题目描述
- 3.2思路分析
- 3.3代码实现
- 浮点数二分
- 题目二
- 3.1题目描述
- 3.2思路分析
- 3.3代码实现
- 四、高精度加法
- 核心模板
- 4.1题目描述
- 4.2思路分析
- 4.3代码实现
- 五、高精度减法
- 核心模板
- 5.1题目描述
- 5.2思路分析
- 5.3代码实现
- 六、高精度乘法(高精度乘低精度)
- 核心模板
- 6.1题目描述
- 6.2思路分析
- 6.3代码实现
- 七、高精度除法(高精度除低精度)
- 核心模板
- 7.1题目描述
- 7.2思路分析
- 7.3代码实现
- 八、一维前缀和
- 核心模板
- 8.1题目描述
- 8.2思路分析
- 8.3代码实现
- 九、二维前缀和
- 核心模板
- 9.1题目描述
- 9.2思路分析
- 9.3代码实现
- 十、一维差分
- 核心模板
- 10.1题目描述
- 10.2思路分析
- 10.3代码实现
- 十一、二维差分
- 核心模板
- 11.1题目描述
- 11.2思路分析
- 11.3代码实现
- 十二、位运算
- 核心模板
- 12.1题目描述
- 12.2思路分析
- 12.3代码实现
- 十三、双指针
- 核心模板
- 题目一
- 13.1题目描述
- 13.2思路分析
- 13.3代码实现
- 题目二
- 13.1题目描述
- 13.2思路分析
- 13.3代码实现
- 十四、离散化
- 核心模板
- 14.1题目描述
- 14.2思路分析
- 14.3代码实现
- 十五、区间合并
- 核心模板
- 15.1题目描述
- 15.2思路分析
- 15.3代码实现
- 十六、树状数组(了解)
- 核心模板
- 十七、线段树(了解)
- 核心模板
前言
本专栏文章为本人AcWing算法基础课的学习笔记,课程地址在这。如有侵权,立即删除。
课前温习

课程提要:
- 课上理解算法的 主要思想。
- 课下 背过(能写出来并调试通过即可) 模板。
- 提高熟练度方法:一个模板题 重复3~5次 AC通过。
一、快速排序
基本思想:分治思想
- 确定分界点:
q[l]、q[(l+r)/2]、q[r]、随机划分。上述任意一种划分方式均可。 - 调整区间:使得所有小于等于x的元素在x之前,大于等于x的元素在x之后(保证x左边的数均小于等于x,x右边的数均大于等于x)。
- 递归处理左右两段:(将左右两段排序),处理完后,原序列就变有序。
核心模板
代码基本思路:
注:如果递归变量传的是i,则分界点一定不能选q[l];如果递归变量传的是j,则分界点一定不能选q[r]。否则都会造成死循环。
设置两个指针i和j,分别指向区间左右两边,然后两个指针同时往中间走,如果i指向的值满足小于x则继续走,否则停下;如果j指向的值,满足大于x则继续走,否则停下;当i和j指针都停下后,然后交换i和j所指向元素的位置。直到i与j指针相遇,结束。
void quick_sort(int q[],int l,int r){
//如果当前区间只有一个数或者没有数,不用排序,直接返回
if(l>=r) return;
//确定分界点,指针指向
int x=q[l+r>>1],i=l-1,j=r+1;
//前后指针遍历数组
while(i<j){
do i++;while(q[i]<x);
do j--;while(q[j]>x);
if(i<j) swap(q[i],q[j]);
}
//递归处理左右两边
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
题目链接:785. 快速排序
1.1题目描述
给定你一个长度为 n 的整数数列。
请你使用快速排序对这个数列按照 从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n。
第二行包含 n 个整数(所有整数均在 1∼109 范围内),表示整个数列。
输出格式
输出共一行,包含 n 个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
5 3 1 2 4 5输出样例:
1 2 3 4 5
1.2思路分析
套用模板即可,注意细节。
1.3代码实现
#include <iostream>
using namespace std;
const int N=1e6+10;
int n;
int q[N];
void quick_sort(int q[],int l,int r){
if(l>=r) return;
int x=q[l+r>>1],i=l-1,j=r+1;
while(i<j){
do i++;while(q[i]<x);
do j--;while(q[j]>x);
if(i<j) swap(q[i],q[j]);
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>q[i];
}
quick_sort(q,0,n-1);
for(int i=0;i<n;i++){
cout<<q[i]<<" ";
}
return 0;
}
二、归并排序
基本思想:分治思想
- 确定分界点:将序列从中间分成两个部分(
mid=(l+r)/2)。 - 递归排序左右两部分。
- 将 左右两部分归并,将两部分合二为一。
注:排序稳定性:元素值相同在排完序之后的相对位置是否会变化。快排不稳定,归并排序稳定。
核心模板
代码基本思路:
合并方法:分别有两个指针指向两个序列的头部,比较指向元素的大小,指向元素小的将元素放进合并数组中,然后再移动已输出元素序列的指针,重复上述步骤。直至某个序列被遍历完,然后把另一个序列剩余元素添在合并数组尾部即可。
void msort(int q[],int l,int r){
//如果当前区间只有一个数或者没有数,不用排序,直接返回
if(l>=r) return ;
int mid=l+r>>1; //取当前区间中点
msort(q,l,mid); //递归排序左边
msort(q,mid+1,r); //递归排序右边
//归并过程
int k=0,i=l,j=mid+1; //i和j分别指向左右两边的起点
//每次将两个指针指向的值小的元素放入结果数组
while(i<=mid&&j<=r){
if(q[i]<=q[j]) temp[k++]=q[i++];
else temp[k++]=q[j++];
}
//如果某一半边没有遍历完,直接把剩余元素加到数组尾部
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
//将结果数组赋值给q数组
for(i=l,j=0;i<=r;i++,j++){
q[i]=temp[j];
}
}
题目链接:787. 归并排序
2.1题目描述
给定你一个长度为 n 的整数数列。
请你使用归并排序对这个数列按照 从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n。
第二行包含 n 个整数(所有整数均在 1∼109 范围内),表示整个数列。
输出格式
输出共一行,包含 n 个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
5 3 1 2 4 5输出样例:
1 2 3 4 5
2.2思路分析
套用模板即可,注意细节。
2.3代码实现
#include <iostream>
using namespace std;
const int N=1e6+10;
int n;
int q[N],temp[N];
void msort(int q[],int l,int r){
if(l>=r) return ;
int mid=l+r>>1;
msort(q,l,mid);
msort(q,mid+1,r);
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r){
if(q[i]<=q[j]) temp[k++]=q[i++];
else temp[k++]=q[j++];
}
while(i<=mid) temp[k++]=q[i++];
while(j<=r) temp[k++]=q[j++];
for(i=l,j=0;i<=r;i++,j++){
q[i]=temp[j];
}
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>q[i];
}
msort(q,0,n-1);
for(int i=0;i<n;i++){
cout<<q[i]<<" ";
}
return 0;
}
三、二分查找
是否具有二段性(即一半区间满足,另一半区间不满足),若具有二段性可以二分。
注:有单调性一定可以二分,没有单调性也有可能可以二分。
二分的本质:寻找满足某种性质的边界点,该性质将区间一分为二(满足或不满足,两种情况)。
做题步骤:
做题首先写一个mid,想check函数或者是一个条件,根据此条件来判断如何划分下一次二分区间,如果是l=mid,则mid后+1;如果是r=mid,则不需要+1。
整数二分
check函数:
bool check(int x){ }//x是否满足某种性质,可写为函数或直接当成条件写在if中。
模板1:
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int b1(int l,int r){
while(l<r){
int mid=l+r>>1; //注意别把这条语句写到循环外,否则死循环
if(check(mid)) r=mid;
else l=mid+1;
}
return l;
}
模板2:
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int b2(int l,int r){
while(l<r){
int mid=l+r+1>>1; //注意别把这条语句写到循环外,否则死循环
if(check(mid)) l=mid;
else r=mid-1;
}
return l;
}
题目一
题目链接: 789. 数的范围
3.1题目描述
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回
-1 -1。输入格式
第一行包含整数 n 和 q ,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回
-1 -1。数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3 1 2 2 3 3 4 3 4 5输出样例:
3 4 5 5 -1 -1
3.2思路分析
应用二分模板即可,注意细节。
3.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int q[N];
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>q[i];
}
while(m--){
int x;
cin>>x;
//查找左端点
int l=0,r=n-1;
while(l<r){
int mid=l+r>>1;
if(q[mid]>=x) r=mid; //如果满足if条件,则x在左半边区间[l,mid]中
else l=mid+1; //否则在右半边区间[mid+1,r]中
}
//如果没有找到,按题目要求输出
if(q[l]!=x) cout<<"-1 -1"<<endl;
else{
cout<<l<<' ';
//查找右端点
int l=0,r=n-1;
while(l<r){
int mid=l+r+1>>1;
if(q[mid]<=x) l=mid; //如果满足if条件,则x在[mid,r]中
else r=mid-1;
}
cout<<l<<endl;
}
}
return 0;
}
浮点数二分
bool check(double x){ }//x是否满足某种性质,可写为函数或直接当成条件写在if中。
或
bool check(float x){ }//x是否满足某种性质,可写为函数或直接当成条件写在if中。
double b3(double l,double r){
const double eps=1e-6;//eps表示精度,取决于题目对精度的要求
while(r-l>eps){
double mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid;
}
return l;
}
题目二
例:求数的平方根
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HOsIwH9b-1687956520550)(https://note.youdao.com/yws/res/4389/WEBRESOURCE14635440587a89ebb8802161f4f78b4f)]](https://img-blog.csdnimg.cn/50d76e97ec564cc4bb98af232a2b666a.png)
注:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uzIhqNAh-1687956520551)(https://note.youdao.com/yws/res/4391/WEBRESOURCEe57276fdef44f95522cae18f58083212)]](https://img-blog.csdnimg.cn/a9536c451e624c8ba4c279fbfe7fe6c0.png)
题目链接:
790. 数的三次方根
3.1题目描述
给定一个浮点数 n ,求它的 三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00输出样例:
10.000000
3.2思路分析
直接套用模板即可,注意细节。
3.3代码实现
待更~
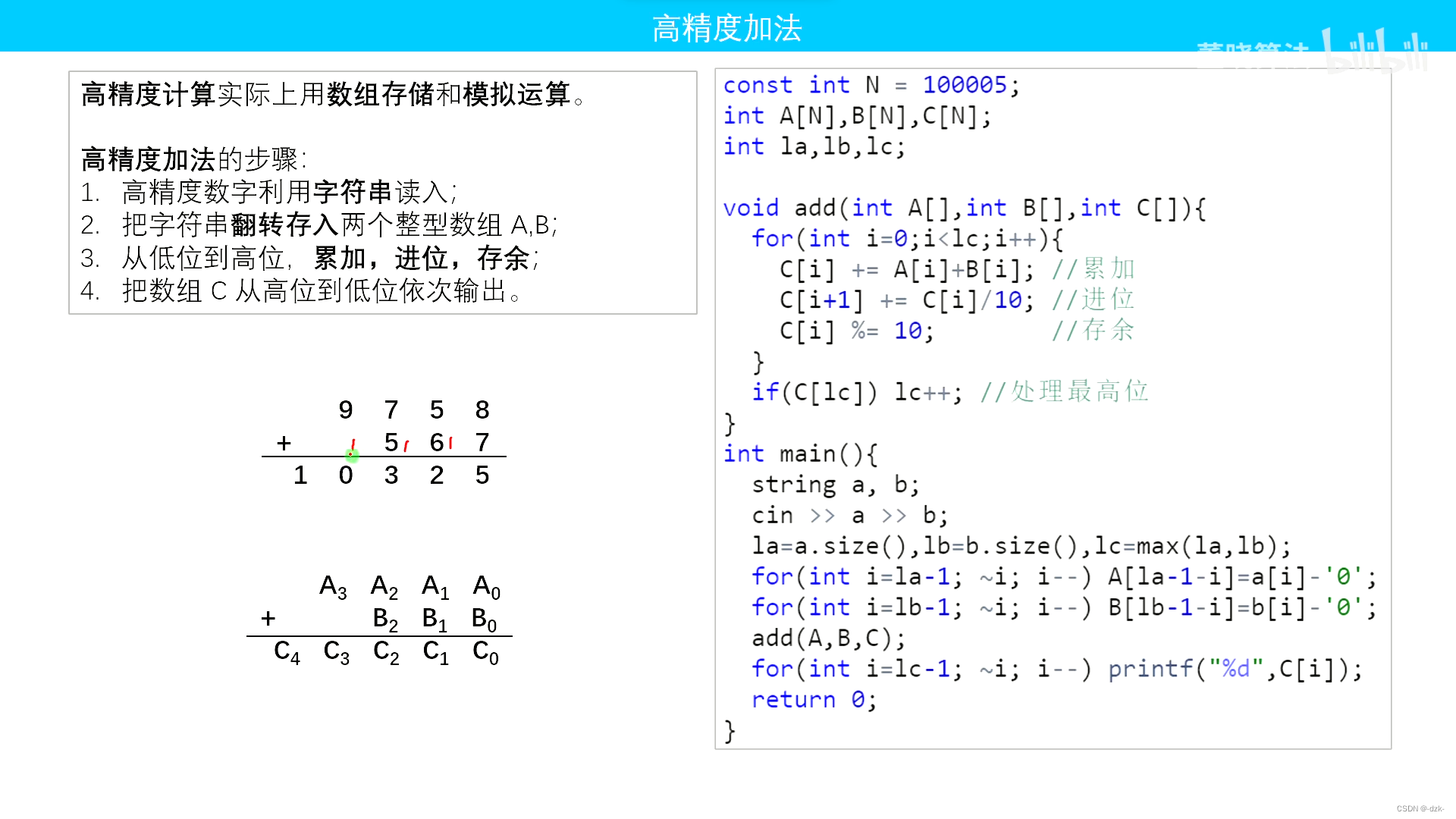
四、高精度加法
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iEMsz6Lx-1687956520551)(https://note.youdao.com/yws/res/3137/WEBRESOURCE6f942f306fd60382d9387b3e256c3c08)]](https://img-blog.csdnimg.cn/a7a09624f561405999f8b5bd1adee773.png)
- 用 字符串 读入数字,用数组 倒序 存储每位,方便进位。
- 下图来源:这里。侵删。
核心模板
//C=A+B,A>=0,B>=0
vector<int> add(vector<int>&A,vector<int>&B){
if(A.size()<B.size()) return add(B,A);
vector<int> C;
int t=0;
for(int i=0;i<A.size();i++){
t+=A[i];
if(i<B.size()) t+=B[i];
C.push_back(t%10);
t/=10;
}
if(t) C.push_back(t);
//去除前导0
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
题目链接:791. 高精度加法
4.1题目描述
给定两个 正整数(不含前导 0),计算它们的和。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的和。
数据范围
1≤整数长度≤100000
输入样例:
12 23输出样例:
35
4.2思路分析
模拟加法过程即可,注意细节,具体见代码注释。
4.3代码实现
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<int> add(vector<int> &A,vector<int> &B){
vector<int> C;
int t=0; //记录每次的进位
//从个位开始依次按加法原则进行模拟
for(int i=0;i<A.size()||i<B.size();i++){
//下两行t记录不进位时当前位计算结果
if(i<A.size()) t+=A[i];
if(i<B.size()) t+=B[i];
C.push_back(t%10); //将当前位进位后计算结果记入C数组中
t/=10; //记录进位
}
if(t) C.push_back(1); //如果A,B均遍历完,还有进位,则在最高位补1
return C;
}
int main()
{ string a,b;
vector<int> A,B;
cin>>a>>b; //a,b正序读入
//逆序存储a,b每位数字
for(int i=a.size()-1;i>=0;i--){
A.push_back(a[i]-'0');
}
for(int i=b.size()-1;i>=0;i--){
B.push_back(b[i]-'0');
}
vector<int> C=add(A,B);
//倒序存储,需倒序输出
for(int i=C.size()-1;i>=0;i--){
cout<<C[i];
}
return 0;
}
五、高精度减法
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yO6a7gtl-1687956520552)(https://note.youdao.com/yws/res/3151/WEBRESOURCEdeeb5ef831401482686875c421f648de)]](https://img-blog.csdnimg.cn/e08533489e59444e8402cb1b4d3fb235.png)
核心模板
//C=A-B,满足A>=B,A>=0,B>=0;
vector<int> sub(vector<int>&A,vector<int>&B){
vector<int> C;
for(int i=0,t=0;i<A.size(),i++){
t=A[i]-t;
if(i<B.size()) t-=B[i];
C.push_back((t+10)%10);
if(t<0) t=1;
else t=0;
}
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
题目链接:792. 高精度减法
5.1题目描述
给定两个 正整数(不含前导 0),计算它们的差,计算结果可能为负数。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的差。
数据范围
1≤整数长度≤105
输入样例:
32 11输出样例:
21
5.2思路分析
模拟减法过程即可,注意细节,具体见代码注释。
5.3代码实现
#include <iostream>
#include <string>
#include <vector>
using namespace std;
//判断是否有A>=B
bool cmp(vector<int> &A,vector<int> &B){
//若A,B位数不同,直接比较位数
if(A.size()!=B.size()) return A.size()>B.size();
//如果A,B位数相同从高位开始逐位数字比较
for(int i=A.size()-1;i>=0;i--){
if(A[i]!=B[i]){
return A[i]>B[i];
}
}
//如果A和B相等,返回true
return true;
}
vector<int> sub(vector<int> &A,vector<int> &B){
vector<int> C;
int t=0; //判断是否需要借位
//从个位开始依次按减法原则进行模拟
//减法已保证A的长度大于等于B的长度,直接枚举A每位数字即可
for(int i=0;i<A.size();i++){
//下两行t记录不借位时当前位计算结果
t=A[i]-t;
if(i<B.size()) t-=B[i];
C.push_back((t+10)%10); //将当前位借位后计算结果记入C数组中 //将t>=0(够减)和t<0(不够减)两种情况合二为一
if(t<0) t=1; //如果不够减需要借位(下次循环时就将下一位减去借位1,再计算当前位结果)
else t=0;
}
//去除前导0
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main()
{ string a,b;
vector<int> A,B;
cin>>a>>b; //a,b正序读入
//逆序存储a,b每位数字
for(int i=a.size()-1;i>=0;i--){
A.push_back(a[i]-'0');
}
for(int i=b.size()-1;i>=0;i--){
B.push_back(b[i]-'0');
}
//计算减法需保证大的数减去小的数,若数据正好符合,则直接相减,否则用大的数减去小的数,然后加负号
if(cmp(A,B)){
vector<int> C=sub(A,B);
//倒序存储,需倒序输出
for(int i=C.size()-1;i>=0;i--){
cout<<C[i];
}
}
else{
vector<int> C=sub(B,A);
cout<<"-";
//倒序存储,需倒序输出
for(int i=C.size()-1;i>=0;i--){
cout<<C[i];
}
}
return 0;
}
六、高精度乘法(高精度乘低精度)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GKuD1ejC-1687956520552)(https://note.youdao.com/yws/res/3376/WEBRESOURCEcfaa84ff1a5883bad29c73e5d03351d5)]](https://img-blog.csdnimg.cn/a8b73bb36b774370ad9c41062b5f9c4d.png)
将低精度作为 整体 来按乘法原则计算、进位。
核心模板
//C=A*b,A>=0,b>=0
vector<int> mul(vector<int>&A,int b){
vector<int> C;
int t=0;
for(int i=0;i<A.size()||t;i++){
if(i<A.size()) t+=A[i]*b;
C.push_back(t%10);
t/=10;
}
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
题目链接:793. 高精度乘法
6.1题目描述
给定两个非负整数(不含前导 0) A 和 B,请你 计算 A×B 的值。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共一行,包含 A×B 的值。
数据范围
1≤A的长度≤100000,0≤B≤10000
输入样例:
2 3输出样例:
6
6.2思路分析
模拟乘法过程即可,注意 将b看做整体去乘,具体见代码注释。
6.3代码实现
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<int> mul(vector<int> &A,int b){
vector<int> C;
int t=0; //记录进位
//从个位开始依次按乘法原则进行模拟
for(int i=0;i<A.size();i++){
t+=A[i]*b; //此时t记录当前位不进位时计算结果
C.push_back(t%10); //将当前位进位后计算结果记入C数组中
t/=10; //记录进位(低位到高位权重多10)
}
//如果遍历完A还有进位,则在最高位添上进位(如果有多位数,直接将进位存储在了一个数组元素中和模板中多出来的进位每个数字存储在一个数组元素中一样,不影响结果)
if(t) C.push_back(t);
//去除前导0
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main()
{ string a;
int b;
vector<int> A;
cin>>a>>b; //a,b正序读入
//逆序存储a每位数字
for(int i=a.size()-1;i>=0;i--){
A.push_back(a[i]-'0');
}
vector<int> C=mul(A,b);
for(int i=C.size()-1;i>=0;i--){
cout<<C[i];
}
return 0;
}
七、高精度除法(高精度除低精度)
核心模板
除法是从最高位开始算,可以正序存储,但是为了与加减乘统一,以及题目中存在四则运算时比较方便,也使用倒序存储每位信息。
//A/b=C...r,A>=0,b>0
vector<int> div(vector<int> &A,int b,int &r){
vector<int>C;
r=0;
for(int i=A.size()-1;i>=0;i--){
r=r*10+A[i];
C.push_back(r/b);
r%=b;
}
reverse(C.begin(),C.end());
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
题目链接:794. 高精度除法
7.1题目描述
给定两个非负整数(不含前导 0) A,B,请你 计算 A/B 的商和余数。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共两行,第一行输出所求的商,第二行输出所求余数。
数据范围
1≤A的长度≤100000,1≤B≤10000
B 一定不为 0输入样例:
7 2输出样例:
3 1
7.2思路分析
模拟减法过程即可,注意细节,具体见代码注释。
7.3代码实现
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> div(vector<int> &A,int b,int &r){ //r是引用
r=0; //记录余数
vector<int> C; //商
//从最高位开始依次按除法原则进行模拟
for(int i=A.size()-1;i>=0;i--){
r=r*10+A[i]; //上一次余数*10和当前位的和,作为本次的被除数
C.push_back(r/b); //当前位计算所得商
r%=b; //当前位计算所得余数
}
//C中为正序存储,为统一,翻转C改为逆序存储
reverse(C.begin(),C.end());
//去除前导0
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main()
{ string a;
int b;
vector<int> A;
cin>>a>>b; //a,b正序读入
//逆序存储a每位数字
for(int i=a.size()-1;i>=0;i--){
A.push_back(a[i]-'0');
}
int r;
vector<int> C=div(A,b,r);
for(int i=C.size()-1;i>=0;i--){
cout<<C[i];
}
cout<<endl<<r;
return 0;
}
八、一维前缀和
前缀和下标从1开始, S[0]=0 ,为更好处理边界
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N0xivW4V-1687956520553)(https://note.youdao.com/yws/res/3410/WEBRESOURCE48030c65b5a740e53add8890f8f279e7)]](https://img-blog.csdnimg.cn/21bf931a142e49f18c4908e02fbc7bee.png)
核心模板
S[]前缀和数组
S[i]=a[1]+a[2]+...+a[i]
a[l]+...+a[r]=S[r]-S[l-1]
题目链接:795. 前缀和
8.1题目描述
输入一个长度为 n 的整数序列。接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出 原序列中从第 l 个数到第 r 个数的和。输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数 l 和 r,表示一个询问的区间范围。输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,1≤n,m≤100000,−1000≤数列中元素的值≤1000
输入样例:
5 3 2 1 3 6 4 1 2 1 3 2 4输出样例:
3 6 10
8.2思路分析
套用公式(模板)即可,注意细节。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wg1INTJa-1687956520553)(https://note.youdao.com/yws/res/5074/WEBRESOURCE5aed1218dec9859076a08819be16eeab)]](https://img-blog.csdnimg.cn/4c47e524a3aa477288027e491879727e.png)
8.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int a[N],s[N];
int main()
{ cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
//套用公式(模板)即可
//前缀和的初始化
for(int i=1;i<=n;i++){
s[i]=s[i-1]+a[i];
}
int l,r;
while(m--){
cin>>l>>r;
//区间和的计算
cout<<s[r]-s[l-1]<<endl;
}
return 0;
}
九、二维前缀和
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4AaKoaF7-1687956520553)(https://note.youdao.com/yws/res/3484/WEBRESOURCEfc6424412c14f32d6756bd97c9f94979)]](https://img-blog.csdnimg.cn/af25863d12a243a9b977acd411f789ca.png)
核心模板
S[]前缀和数组
S[i][j]=第i行第j列格子左上部分所有元素的和
以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵的和为:
S[x2][y2]-S[x1-1][y2]-S[x2][y1-1]+S[x1-1][y1-1]
题目链接:796. 子矩阵的和
9.1题目描述
输入一个 n 行 m 列的整数矩阵,再输入 q 个询问,每个询问包含四个整数 x1,y1,x2,y2 ,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问 输出子矩阵中所有数的和。输入格式
第一行包含三个整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含四个整数 x1,y1,x2,y2 ,表示一组询问。输出格式
共 q 行,每行输出一个询问的结果。
数据范围
1≤n,m≤1000,1≤q≤200000,1≤x1≤x2≤n,1≤y1≤y2≤m,−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3 1 7 2 4 3 6 2 8 2 1 2 3 1 1 2 2 2 1 3 4 1 3 3 4输出样例:
17 27 21
9.2思路分析
套用公式(模板)即可,注意细节。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3Y3evBWA-1687956520554)(https://note.youdao.com/yws/res/5085/WEBRESOURCE2f15f63cdf40361cdd27558ca83fcd9e)]](https://img-blog.csdnimg.cn/54a52fe5644046a28d97a16969b79170.png)
计算红方框前缀和,左上角(x1,y1),右下角(x2,y2)
此方阵代表a[][]数组
-
s[x2][y2]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rng9tlP1-1687956520554)(https://note.youdao.com/yws/res/5076/WEBRESOURCE572e5adda3f774b7f7eb9df96c6b2127)]](https://img-blog.csdnimg.cn/d01f1c22468e4ccbb3d342d3f84e2174.png)
-
s[x2][y2]-s[x1-1][y2]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ad1Kp41o-1687956520554)(https://note.youdao.com/yws/res/5078/WEBRESOURCEc1ba35e8726d0014cf31f994f13255ec)]](https://img-blog.csdnimg.cn/3a8af08574754d10ae4d70a656ac52be.png)
-
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1](黑色s[x1-1][y1-1]被减了两次)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6p8NBppR-1687956520555)(https://note.youdao.com/yws/res/5081/WEBRESOURCEb9a402049c9fb1b99b64055374e3b2dd)]](https://img-blog.csdnimg.cn/c9c571c9566540b49b4134c1e3f9dea6.png)
-
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4Xj55cF6-1687956520555)(https://note.youdao.com/yws/res/5083/WEBRESOURCE688cac51d834fe4d3f0e3d1e0e5787c3)]](https://img-blog.csdnimg.cn/187888669ae84d6e9d15956202244b16.png)
计算绿色方框的前缀和s[i][j]
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yNcAKc2o-1687956520556)(https://note.youdao.com/yws/res/5089/WEBRESOURCEfea6f2db004ea2c9e3de9be55e6776d9)]](https://img-blog.csdnimg.cn/a6ecd5ec58924f92808b4632f01c5e1a.png)
-
s[i-1][j](浅蓝区域)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4XgBwzxv-1687956520556)(https://note.youdao.com/yws/res/5091/WEBRESOURCEfb266457fae518bddcea4be248018369)]](https://img-blog.csdnimg.cn/16a75b2480a248b29a492e4914c7f5c6.png)
-
s[i-1][j]+s[i][j-1](浅蓝区域)(深蓝色区域s[i-1][j-1]被加了两次)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aLsD9yDs-1687956520556)(https://note.youdao.com/yws/res/5093/WEBRESOURCE1071fbef7c66b7f58dab2f1671a3ccbf)]](https://img-blog.csdnimg.cn/3c166d02aff74b6096a173bd1986e968.png)
-
s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j](a[i][j]为绿色方格)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-opOuT22r-1687956520557)(https://note.youdao.com/yws/res/5095/WEBRESOURCEe3320339a8e1fc6e1df7c750b277e26d)]](https://img-blog.csdnimg.cn/2fa98a88e41e475a8255127170d9d77f.png)
9.3代码实现
#include <iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],s[N][N];
int main()
{ cin>>n>>m>>q;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
//套用公式(模板)即可
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]; //求前缀和
}
}
int x1,y1,x2,y2;
while(q--){
cin>>x1>>y1>>x2>>y2;
cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl; //算子矩阵的和
}
return 0;
}
十、一维差分
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8SjM1JqN-1687956520557)(https://note.youdao.com/yws/res/3491/WEBRESOURCE634ebe16df850d1f7c718653c8ca871c)]](https://img-blog.csdnimg.cn/5f5e71b9954849c7bd5b2ef58b984355.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Cl6rEjSU-1687956520557)(https://note.youdao.com/yws/res/3493/WEBRESOURCEe4bb8138eb4a77084765681bdb60dca9)]](https://img-blog.csdnimg.cn/1bb9904823a5402186d5f8bb4994ef00.png)
核心模板
B[]差分数组
给区间[l,r]中的每个数加上c:B[l]+=c,B[r+l]-=c
题目链接:797. 差分
10.1题目描述
输入一个长度为 n 的整数序列。
接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示 将序列中 [l,r]之间的每个数加上 c。
请你 输出进行完所有操作后的序列。输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,1≤l≤r≤n,−1000≤c≤1000,−1000≤整数序列中元素的值≤1000
输入样例:
6 3 1 2 2 1 2 1 1 3 1 3 5 1 1 6 1输出样例:
3 4 5 3 4 2
10.2思路分析
套用公式(模板)即可,注意细节。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CBXFitzF-1687956520557)(https://note.youdao.com/yws/res/5280/WEBRESOURCEe0519c104555077ee7f5dbd2614d40dd)]](https://img-blog.csdnimg.cn/d10959e2baa242729373a54190694bcf.png)
10.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int n,m;
int a[N],b[N]; //b为差分数组
void insert(int l,int r,int c){
b[l]+=c;
b[r+1]-=c;
}
int main()
{ cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
//套用公式(模板)即可
//假定a数组初识为0,而a中每个元素相当于在该元素位置加了该元素值
for(int i=1;i<=n;i++){
insert(i,i,a[i]);
}
int l,r,c;
while(m--){
cin>>l>>r>>c;
insert(l,r,c);
}
//差分数组求前缀和得到结果数组
for(int i=1;i<=n;i++){
b[i]+=b[i-1];
}
for(int i=1;i<=n;i++){
cout<<b[i]<<" ";
}
return 0;
}
十一、二维差分
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b1xRzjps-1687956520558)(https://note.youdao.com/yws/res/3496/WEBRESOURCEf9d6807a07a99200c520bab15992e929)]](https://img-blog.csdnimg.cn/d43fdf5d0ba24960a2b66487f23ea41e.png)
核心模板
B[]差分数组
给以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵中所有元素加上c:
B[x1][y1]+=c,B[x2+1][y1]-=c,B[x1][y2+1]-=c,B[x2+1][y2+1]+=c
题目链接:798. 差分矩阵
11.1题目描述
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c ,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的 子矩阵中的每个元素的值加上 c。请你 将进行完所有操作后的矩阵输出。输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,1≤q≤100000,1≤x1≤x2≤n,1≤y1≤y2≤m,−1000≤c≤1000,−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3 1 2 2 1 3 2 2 1 1 1 1 1 1 1 2 2 1 1 3 2 3 2 3 1 3 4 1输出样例:
2 3 4 1 4 3 4 1 2 2 2 2
11.2思路分析
套用公式(模板)即可,注意细节。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KKmJxjGa-1687956520558)(https://note.youdao.com/yws/res/5286/WEBRESOURCEbe57c40dd6125ce9a4e016cb9a392d0d)]](https://img-blog.csdnimg.cn/d9d65f9340ab4965990f9c76c4a2afe3.png)
计算红色区域对应的a[][]的每个数加上c
此方阵代表b[][]数组,红色区域左上角为(x1,y1),右下角为(x2,y2)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sgR3S7hE-1687956520558)(https://note.youdao.com/yws/res/5291/WEBRESOURCE99300d003f3ca65f4a5c48aa5c6ffba9)]](https://img-blog.csdnimg.cn/093fc6f0f4bc4d66a657cd76b850a3e9.png)
-
b[x1][y1]+=c
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HZz58w8V-1687956520558)(https://note.youdao.com/yws/res/5301/WEBRESOURCEd73119a1ef14e9c8739a09ac67329f23)]](https://img-blog.csdnimg.cn/fbac896512cd404094a3d5ed3bb05321.png)
-
b[x1][y1]+=c,b[x1][y2+1]-=c
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ur3uQnjo-1687956520559)(https://note.youdao.com/yws/res/5304/WEBRESOURCE3a6e80435132bc1c0c2876f4233f9ccb)]](https://img-blog.csdnimg.cn/26006a4014894daf8ff1ef6c9ac8fac2.png)
-
b[x1][y1]+=c,b[x1][y2+1]-=c,b[x2+1][y1]-=c(黑色区域被减了两次)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iyskDjeO-1687956520559)(https://note.youdao.com/yws/res/5310/WEBRESOURCE4d97f2d7e4682caa6dc8906d74307952)]](https://img-blog.csdnimg.cn/572a5eabc24241f8ae4465f03751b341.png)
-
b[x1][y1]+=c,b[x1][y2+1]-=c,b[x2+1][y1]-=c,b[x2+1][y2+1]+=c
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RdSghSlx-1687956520559)(https://note.youdao.com/yws/res/5312/WEBRESOURCEa6637d6d75737311545c44e2048c1a08)]](https://img-blog.csdnimg.cn/49ca0739faf34665b6d15c7f26d10c15.png)
11.3代码实现
#include <iostream>
using namespace std;
const int N=1010;
int n,m,q;
int a[N][N],b[N][N]; //b为差分数组
void insert(int x1,int y1,int x2,int y2,int c){
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
int main()
{ cin>>n>>m>>q;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
//套用公式(模板)即可
//假定a数组初始为0,而a中每个元素相当于在该元素位置(大小为1的子矩阵)加了该元素值
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
insert(i,j,i,j,a[i][j]);
}
}
int x1,y1,x2,y2,c;
while(q--){
cin>>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
//差分数组求前缀和得到结果数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout<<b[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
十二、位运算
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FRCPQs2V-1687956520559)(https://note.youdao.com/yws/res/5381/WEBRESOURCEba81a11bb6d2bdd4396a55505e6e4e7f)]](https://img-blog.csdnimg.cn/d0da6f9703ba4464935f43ac75b76986.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4nMSFkaj-1687956520560)(https://note.youdao.com/yws/res/5383/WEBRESOURCEfaff767293f701a38245d6a9430e2c0f)]](https://img-blog.csdnimg.cn/8305259ddf074b8182cd1313eba3ab27.png)
lowbit(x)原理:返回的是x&(~x+1)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XrmLNdhk-1687956520560)(https://note.youdao.com/yws/res/5385/WEBRESOURCEe6897ab95c2be99e076d304f096ef953)]](https://img-blog.csdnimg.cn/2293459dfad846a6bdec7333fd7fe846.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zTQnTw3R-1687956520560)(https://note.youdao.com/yws/res/5390/WEBRESOURCEedb43c97894ca2aad4c11a4223403961)]](https://img-blog.csdnimg.cn/4c1a5e962a974acf839c81a12e1695e4.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gNYoSsVC-1687956520560)(https://note.youdao.com/yws/res/5399/WEBRESOURCEe24c38d50cc91419e98f0b0f9fdee45d)]](https://img-blog.csdnimg.cn/6191d84b6b6c486f9cad32fe1d2ab919.png)
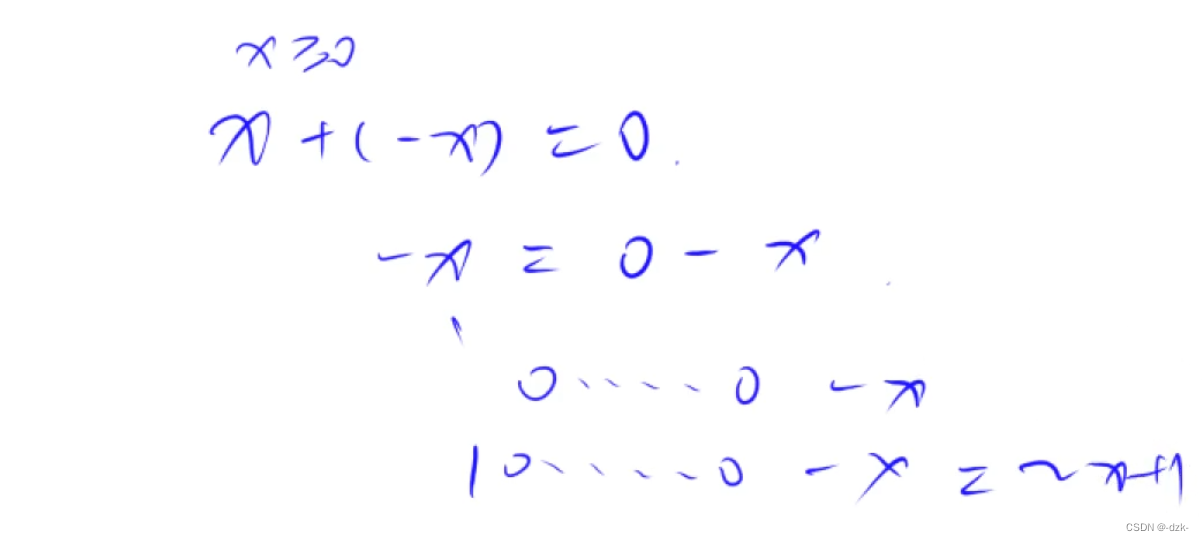
核心模板
求n的第k位数字:n>>k&1
返回n的最后一位:lowbit(n)=n&-n
//lowbit()无头文件,需自己实现函数。
题目链接:801. 二进制中1的个数
12.1题目描述
给定一个长度为 n 的数列,请你求出数列中每个数的二进制表示中 1 的个数 。
输入格式
第一行包含整数 n 。
第二行包含 n 个整数,表示整个数列。
输出格式
共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。
数据范围
1≤n≤100000 , 0≤数列中元素的值≤109
输入样例:
5 1 2 3 4 5输出样例:
1 1 2 1 2
12.2思路分析
使用lowbit()操作,每次将“最后一位1”减去,统计出数中1的个数。
12.3代码实现
#include <iostream>
using namespace std;
const int N=100010;
int a[N];
int n;
int lowbit(int x){
return x&-x;
}
int num(int x){
int sum=0;
while(x){
sum++; //统计1的个数
x-=lowbit(x); //每次减去x的最后一位1
}
return sum;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
for(int i=0;i<n;i++){
cout<<num(a[i])<<' ';
}
return 0;
}
十三、双指针
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CzxLaX5A-1687956520560)(https://note.youdao.com/yws/res/5335/WEBRESOURCEe4b4982498ec6bee511f8c22aa3ece90)]](https://img-blog.csdnimg.cn/47940b280fa943b8910799f6b5f7aa6d.png)
先想暴力做法,然后根据i,j之间是否存在某种单调关系,进行双指针优化。
核心模板
for(int i=0,j=0;i<n;i++){
while(j<i&&check(i,j)) j++;
//具体问题的逻辑
}
//常见问题分类:
(1)对于一个序列,用两个指针维护一段区间。
(2)对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
例子:
输入n个字符串(不含空格),由空格隔开。每行依次输出每个字符串。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z2BpQtPI-1687956520561)(https://note.youdao.com/yws/res/5338/WEBRESOURCE3ab5295541af65967ec70c87335b3e2a)]](https://img-blog.csdnimg.cn/4d5b787fb6494b6580906089e20e2311.png)
思路:i指针指向字符串第一个字母,j向后寻找空格,如果找到,输出位置i到j的字符串,并将i更新为j(下次从空格位置后找下一个字符串),直到将n个字符串输出。
代码:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8z0hzqt8-1687956520561)(https://note.youdao.com/yws/res/5348/WEBRESOURCEb3a3585999915881a3cc9bef848a10fc)]](https://img-blog.csdnimg.cn/5960e42ab7de4670823b0402e3447b5d.png)
题目一
题目链接:799. 最长连续不重复子序列
13.1题目描述
给定一个长度为 n 的整数序列,请找出 最长的不包含重复的数的连续区间,输出 它的长度。
输入格式
第一行包含整数 n 。
第二行包含 n 个整数(均在 0∼105 范围内),表示整数序列。
输出格式
共一行,包含一个整数,表示最长的不包含重复的数的连续区间的长度。
数据范围
1≤n≤105
输入样例:
5 1 2 2 3 5输出样例:
3
13.2思路分析
i枚举区间右端点,j枚举区间左端点。枚举所有可能区间,记录满足条件区间长度的最大值。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1YIVhHcR-1687956520561)(https://note.youdao.com/yws/res/5362/WEBRESOURCE451534fca8d7dfa8e623edf8900c07a9)]](https://img-blog.csdnimg.cn/efedcca20cd6418796c980cff5c2d9e2.png)
优化:
i枚举区间右端点,j枚举区间左端点,每次判断[j,i]区间是否满足条件,如果不满足区间就缩短,即j++。记录满足条件区间的最大长度。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U3u1sbtL-1687956520561)(https://note.youdao.com/yws/res/5371/WEBRESOURCE3835fb5e3a142ae4f8787fde60605920)]](https://img-blog.csdnimg.cn/c2c768a6e51047adbe9d5c17c07a8338.png)
- 对于每次i如果向后移动,则j必定不动或者向后移动,j一定不会向前移动。原因:如果i往后走,假设j往前走,如果找到了满足条件的区间,则这个区间一定满足无重复元素,而且比i在其原来位置找到的区间要长,由于i在原来位置找到最长满足条件区间才向后移,说明原来[j,i]区间就是从j开始到i满足条件的区间长度最大值。若i往后移动,j也往前移动能求得最优区间长度,说明原来[j,i]区间不是i在原位置的区间长度最大(而是[j-x,i],即j应该在求得[j,i]区间中的j的左边),这就互相矛盾了,所以j只能向后或者不动。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N3GOehzW-1687956520562)(https://note.youdao.com/yws/res/5373/WEBRESOURCE73b4113d5ec4fabec5d2d516022567fc)]](https://img-blog.csdnimg.cn/eb0a690435c5473e92c02e61ca09ce1e.png)
s[]记录a[]中每个数出现的个数
双指针执行具体流程:i每次向后移动,同时记录a[i]的值的出现次数在s[i]中,i向后走的过程中,如果s[a[i]]>1,即当前a[i]位置的数不是第一次出现,出现重复了,此时需要缩小区间,将j指向的数的出现次数-1,移动j指针,将j指针依次向后移动,来找到与a[i]重复的位置,如果j已经越过该位置,说明当前区间无重复元素,s[a[i]]<=1,满足题目要求,j停下,此时继续向后移动i指针,重复上述过程,直到遍历完a[]数组。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VHBxBFE7-1687956520562)(https://note.youdao.com/yws/res/5453/WEBRESOURCE02118b4ca7bccb58c8985ddcbd9d63cd)]](https://img-blog.csdnimg.cn/5345b05356fa420d803f89e15f639190.png)
13.3代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N=100010;
int a[N],s[N]; //s[a[i]]存储当前[j,i]区间中a[i]的值出现的次数
int n,ans;
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0,j=0;i<n;i++){
s[a[i]]++; //每次i指向的值的出现次数+1
//循环条件可以不写j<=i,因为j>i时,区间一定满足要求,不会走循环
while(s[a[i]]>1){ //如果此时i指向的值的出现次数>1,说明区间中有重复的值,此时应该缩小区间来去掉重复值
s[a[j]]--; //j指向的元素要出区间,j指向的值的出现次数-1
j++; //j往后移动,缩小区间
}
ans=max(ans,i-j+1); //统计出区间长度的最大值
}
cout<<ans;
return 0;
}
题目二
题目链接:800. 数组元素的目标和
13.1题目描述
给定两个升序排序的有序数组 A 和 B ,以及一个目标值 x 。
数组下标从 0 开始。
请你求出满足
A[i]+B[j]=x的数对 (i,j) 。数据保证有唯一解。
输入格式
第一行包含三个整数 n,m,x ,分别表示 A 的长度,B 的长度以及目标值 x 。
第二行包含 n 个整数,表示数组 A 。
第三行包含 m 个整数,表示数组 B 。
输出格式
共一行,包含两个整数 i 和 j 。
数据范围
数组长度不超过 105 。
同一数组内元素各不相同。
1≤数组元素≤109输入样例:
4 5 6 1 2 4 7 3 4 6 8 9输出样例:
1 1
13.2思路分析
待更~
13.3代码实现
待更~
十四、离散化
对一组值范围比较大而其中出现的数的个数比较少的情况,使用离散化。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wV9D9ZO7-1687956520562)(https://note.youdao.com/yws/res/5630/WEBRESOURCEe1a0904b35e10fd42c2c4fef32d38908)]](https://img-blog.csdnimg.cn/285e8cab11a64938af0f8856d12cc554.png)
第一步,将原数组元素去重;
第二步,用二分来查找每个元素离散化之后的值(离散化后数组元素的下标为离散化后的值,则该数组元素的值为待离散前原数组元素的值)。
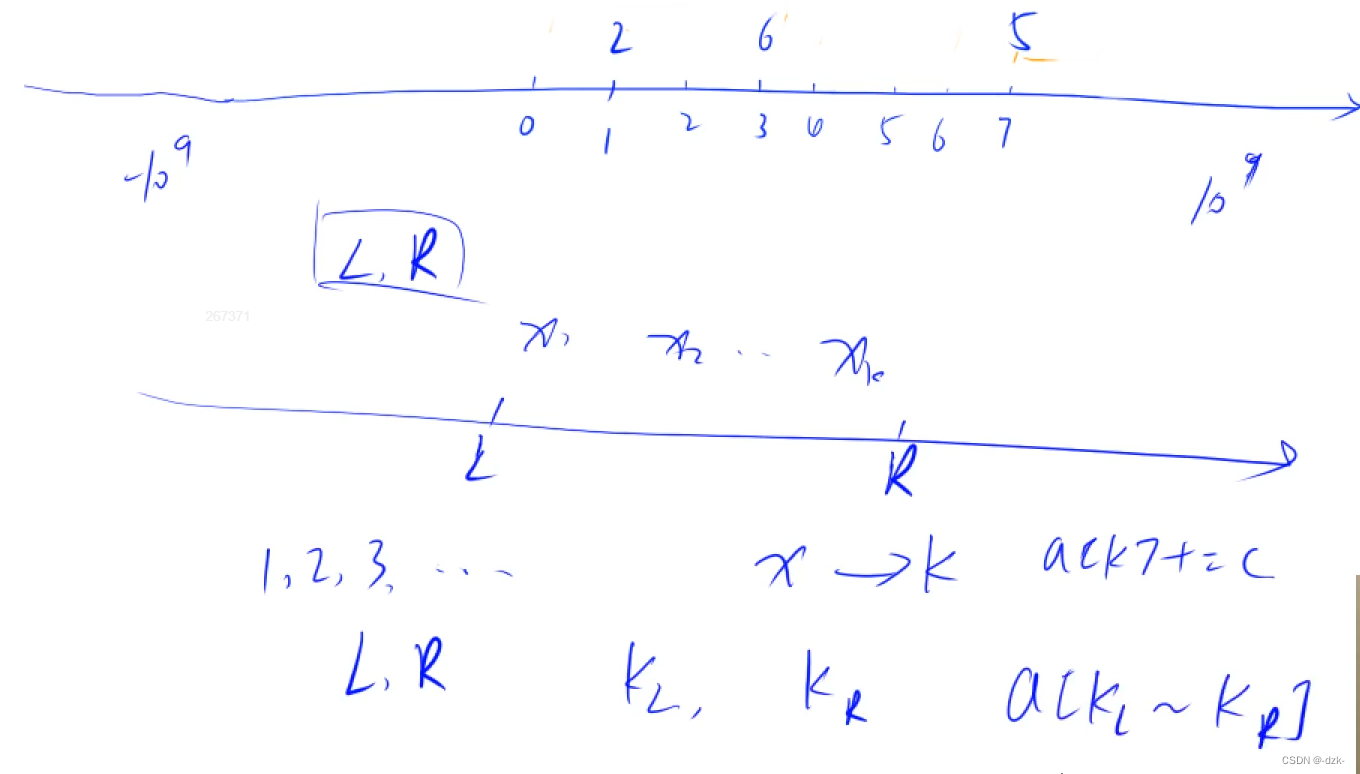
unique自己手写思路:

将序列中第一次出现,而且和它前面的数不相等就把这个数拿出来,将所有满足条件的数拿出来即完成了去重。
手写unique函数代码
vector<int> ::iterator unique(vector<int> &a){
int j=0;
for(int i=0;i<a.size();i++){
if(!i||a[i]!=a[i-1]){
a[j++]=a[i];
}
}
//a[0]~a[j-1] 所有a中不重复的数
return a.begin()+j;
}
核心模板
unqiue作用:unique(a.begin(),a.end())将a数组去重并且返回去重后数组的尾端点。
vector<int> alls; //存储所有待离散化的值
sort(alls.begin(),alls.end());//将所有值排序
alls.erase(unique(alls.begin(),alls.end()),alls.end()); //去掉重复元素
//二分求出x对应的离散化的值
int find(int x){ //找到第一个大于等于x的位置
int l=0,r=alls.size()-1;
while(l<r){
int mid=l+r>>1;
if(alls[mid]>=x) r=mid;
else l=mid+1;
}
return r+1; //映射1,2,...,n;不+1从0开始映射
}
题目链接:802. 区间和
14.1题目描述
假定有一个无限长的数轴,数轴上每个坐标上的数都是 0 。
现在,我们首先进行 n 次操作,每次操作将某一位置 x 上的数加 c 。
接下来,进行 m 次询问,每个询问包含两个整数 l 和 r ,你需要求出在 区间 [l,r] 之间的所有数的和。
输入格式
第一行包含两个整数 n 和 m 。
接下来 n 行,每行包含两个整数 x 和 c 。
再接下来 m 行,每行包含两个整数 l 和 r 。
输出格式
共 m 行,每行输出一个询问中所求的区间内数字和。
数据范围
−109≤x≤109,1≤n,m≤105,−109≤l≤r≤109,−10000≤c≤10000
输入样例:
3 3 1 2 3 6 7 5 1 3 4 6 7 8输出样例:
8 0 5
14.2思路分析
套用模板即可,注意细节。
14.3代码实现
#include <iostream>
#include <vector>
#include <utility>
#include <algorithm>
using namespace std;
const int N=300010;
typedef pair<int,int> PII;
int n,m;
int a[N],s[N]; //a[]存储每个数,s[]存储前缀和
vector<int> alls; //存储待离散的值
vector<PII> add,query; //存储操作
//二分查找x离散化后的结果
int find(int x){
int l=0,r=alls.size()-1;
while(l<r){
int mid=l+r>>1;
if(alls[mid]>=x) r=mid;
else l=mid+1;
}
return r+1; //将x映射成从1开始的下标
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
int x,c;
cin>>x>>c;
add.push_back({x,c});
alls.push_back(x);
}
for(int i=0;i<m;i++){
int l,r;
cin>>l>>r;
query.push_back({l,r});
alls.push_back(l);
alls.push_back(r);
}
//去重
sort(alls.begin(),alls.end());
alls.erase(unique(alls.begin(),alls.end()),alls.end());
//处理插入
for(auto item:add){
int x=find(item.first);
a[x]+=item.second; //将插入的数,放到其离散化后的位置上,注意是+=,因为同一个数会出现多次,要求区间和的时候,得将它们都加上
}
//预处理前缀和
for(int i=1;i<=alls.size();i++) s[i]=s[i-1]+a[i];
//处理询问
for(auto item:query){
int l=find(item.first),r=find(item.second);
cout<<s[r]-s[l-1]<<endl;
}
return 0;
}
十五、区间合并
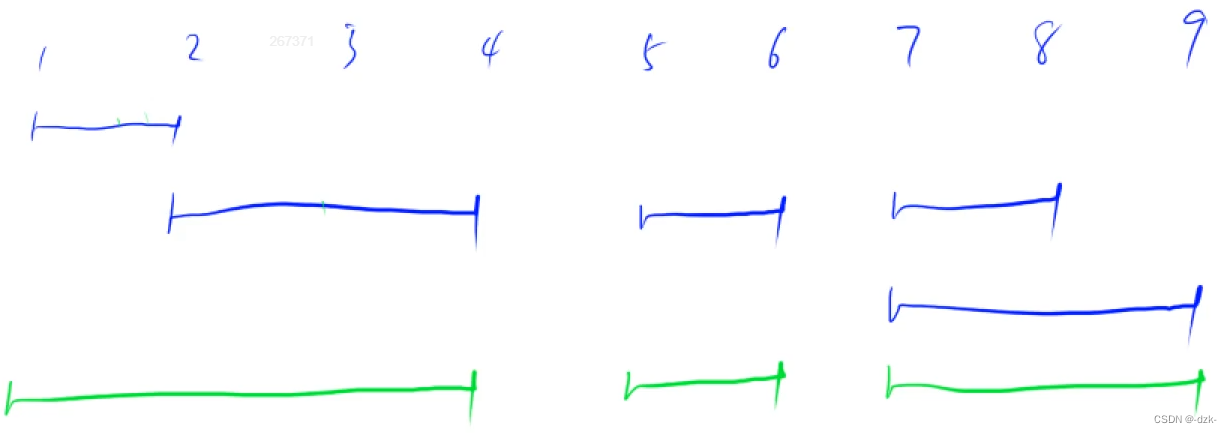

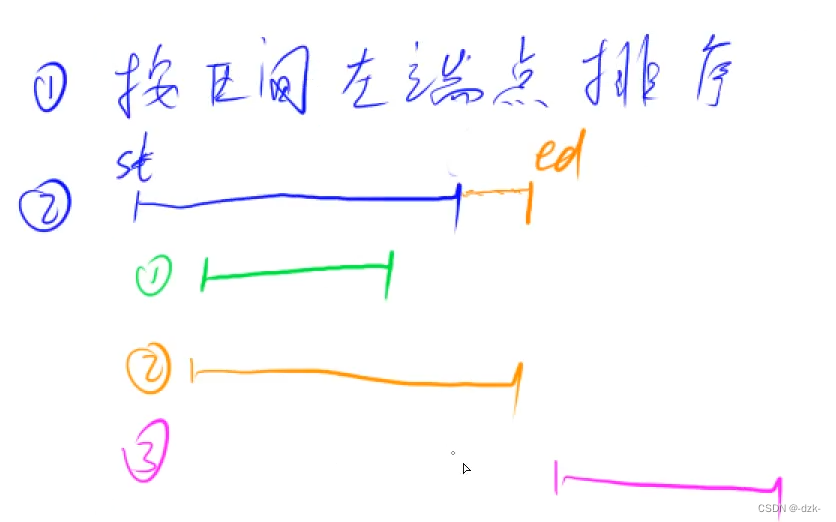
- 将区间按左端点排序。
- 区间情况数如图三种,第一种和第三种不需要改变原来需要维护的区间,第二种需要把原有区间延长至新的ed。
- 如果前两种情况都已处理,只剩下第三种情况(区间st比原需维护的区间的ed还要大),原需维护区间不会再与第三种情况的区间及其后面的区间有交集,所以将原需维护的区间放入答案中取,然后将其更新为第三种情况的第一个这样的区间,再进行后续合并操作。
核心模板
//将所有存在交集的区间合并
void merge(vector<PII> &segs){
vector<PII> res;
sort(segs.begin(),segs.end());
int st=-2e9,ed=-2e9; //按题目要求设置边界即可
for(auto seg:segs){
if(ed<seg.first){
if(st!=-2e9) res.push_back({st,ed});
st=seg.first,ed=seg.second;
}
else ed=max(ed,seg.second); }
if(st!=-2e9) res.push_back({st,ed});
segs=res;
}
题目链接:803. 区间合并
15.1题目描述
给定 n 个区间 [li,ri] ,要求合并所有有交集的区间。
注意如果在端点处相交,也算有交集。
输出合并完成后的 区间个数。
例如:[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 l 和 r。
输出格式
共一行,包含一个整数,表示合并区间完成后的区间个数。
数据范围
1≤n≤100000,−109≤li≤ri≤109
输入样例:
5 1 2 2 4 5 6 7 8 7 9输出样例:
3
15.2思路分析
套用模板即可,注意细节。
15.3代码实现
#include <iostream>
#include <utility>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int,int> PII;
const int N=100010;
int n;
vector<PII> v; //存储每个区间,first为左端点,second为右端点
void merge(vector<PII> &v){
vector<PII> ans; //存储合并后的区间结果
sort(v.begin(),v.end()); //默认按区间左端点(first)从小到大排序
int st=-2e9, ed=-2e9; //设置边界值,即初始化不存在合法区间
//遍历所有区间
for(auto i:v){
//如果是第三种情况,即当前区间的左端点比原维护区间的右端点大,不需要合并
if(ed<i.first){
//要特判,如果是初始化的区间则不放入数组
if(st!=-2e9){
ans.push_back({i.first,i.second});
}
st=i.first,ed=i.second; //将需维护区间更新为当前枚举的区间
}
//如果是第二种情况,说明区间有交集,则将原需维护区间的右端点和枚举区间的右端点取max
else ed=max(ed,i.second);
}
//防止输入的为空数组,需特别判断一下
if(st!=-2e9) ans.push_back({st,ed});
v=ans;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){
int l,r;
cin>>l>>r;
v.push_back({l,r});
}
merge(v);
cout<<v.size();
return 0;
}
以下内容为拓展内容
十六、树状数组(了解)
- 下图内容作者如图。侵删。


树状数组主要用于查询前缀和、区间和及点更新,对点查询、区间修改效率较低。 - 下述图片内容来源这里。侵删。


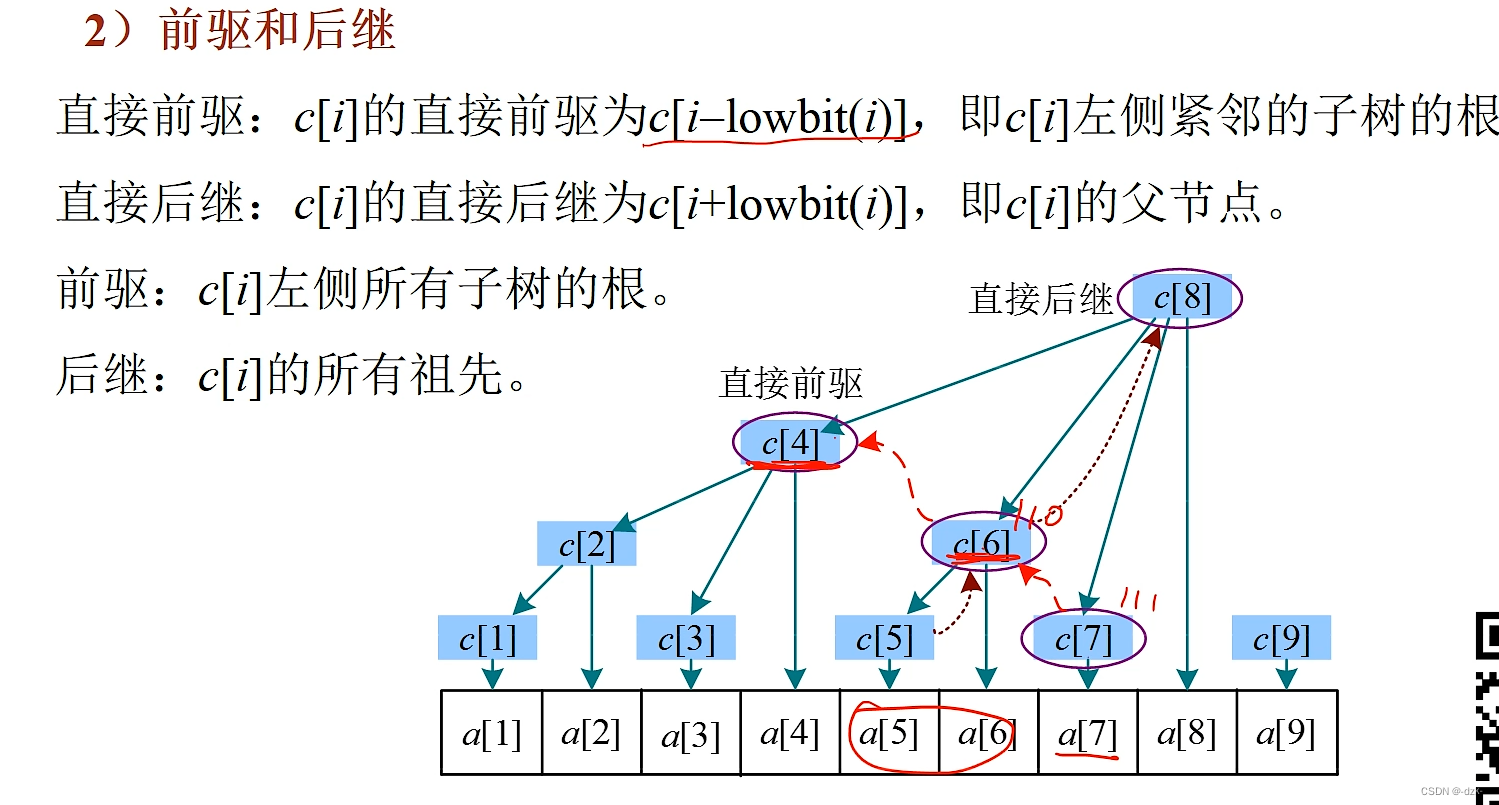
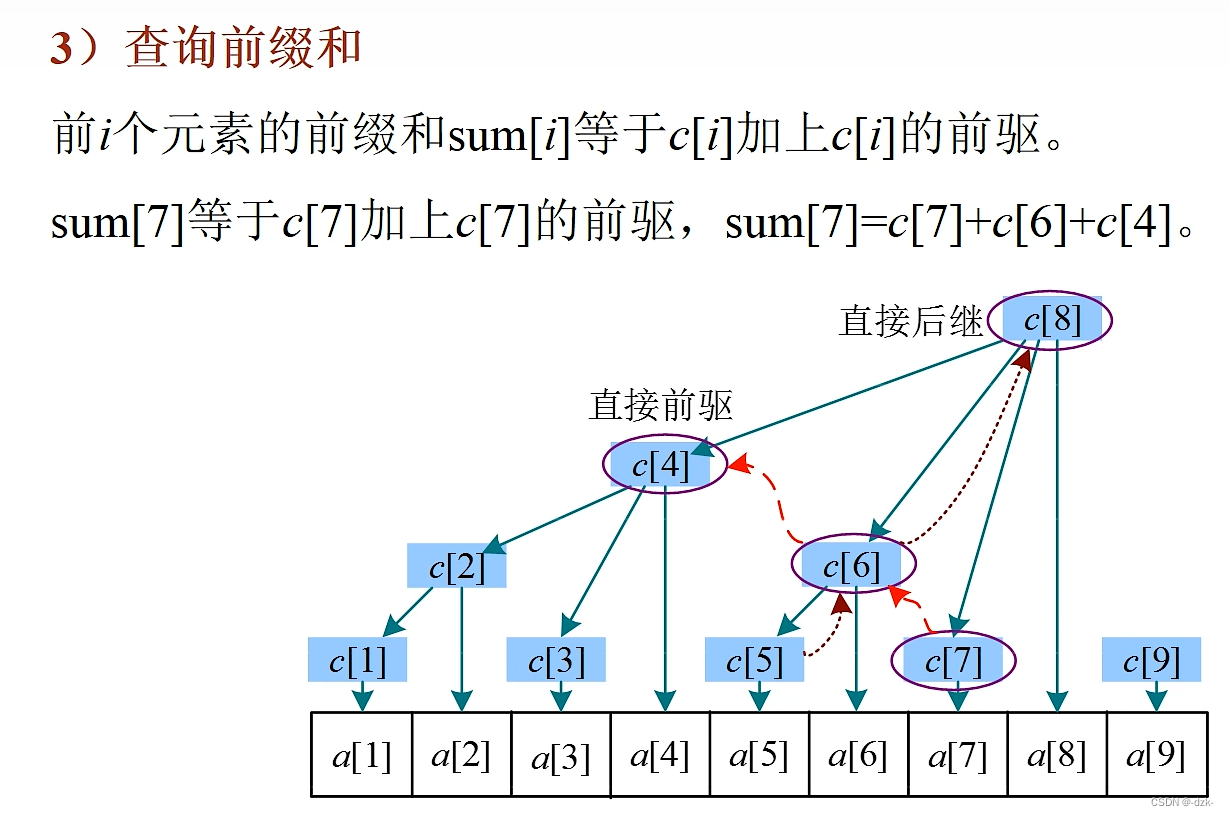
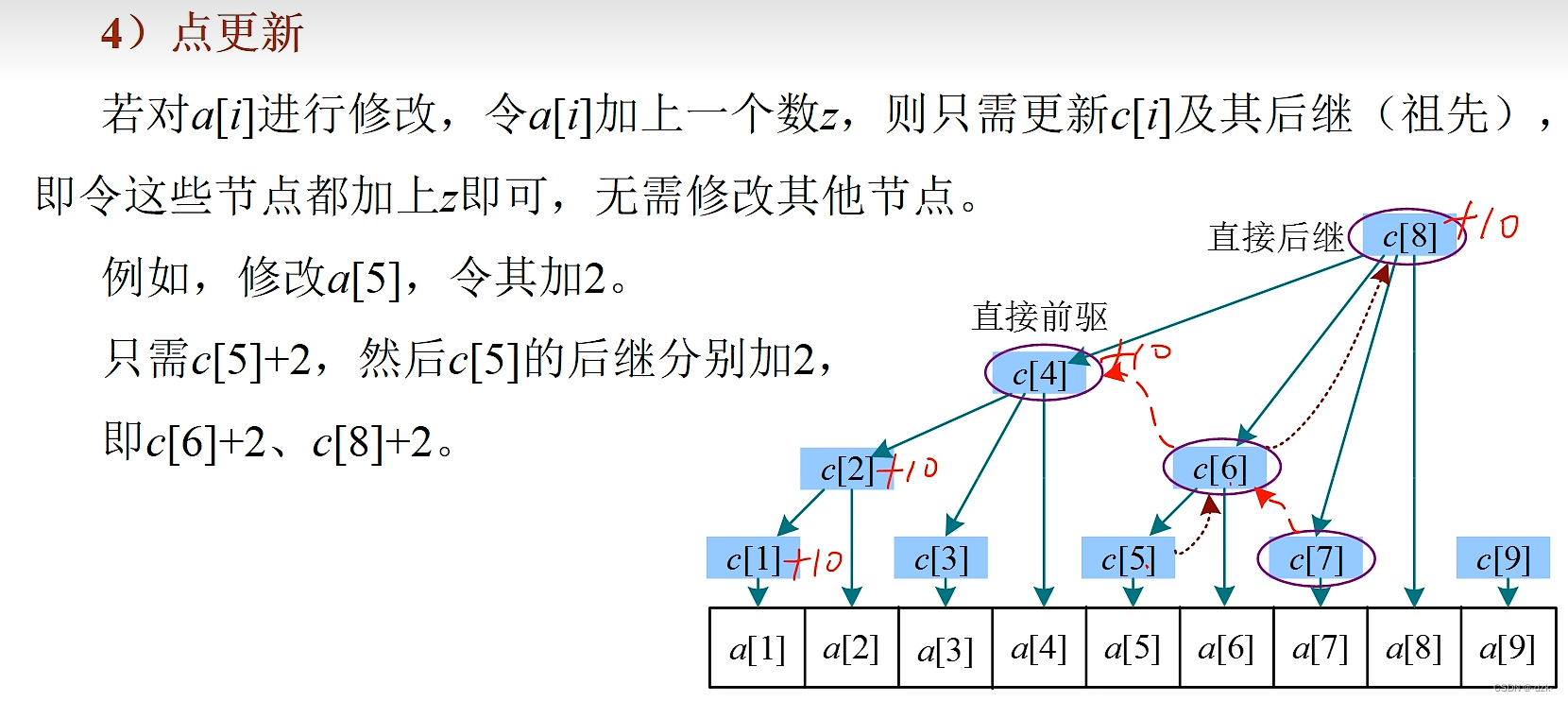

核心模板
//树状数组长度是固定的,为n+1
//树状数组的下标必须从1开始(下标为0会死循环)
int tr[n+1];
//求最低位的一位1
int lowbit(int x){
return x&-x;
}
//点更新:在tr[x]的位置上加上c
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i))
tr[i]+=c;
}
//查询前缀和
int query(int x){
int res=0;
for(int i=x;i>0;i-=lowbit(i))
res+=tr[i];
return res;
}
//区间和
int sum(int i,int j){
return query(j)-query(i-1);
}
十七、线段树(了解)
- 下述图片内容来源这里。侵删。
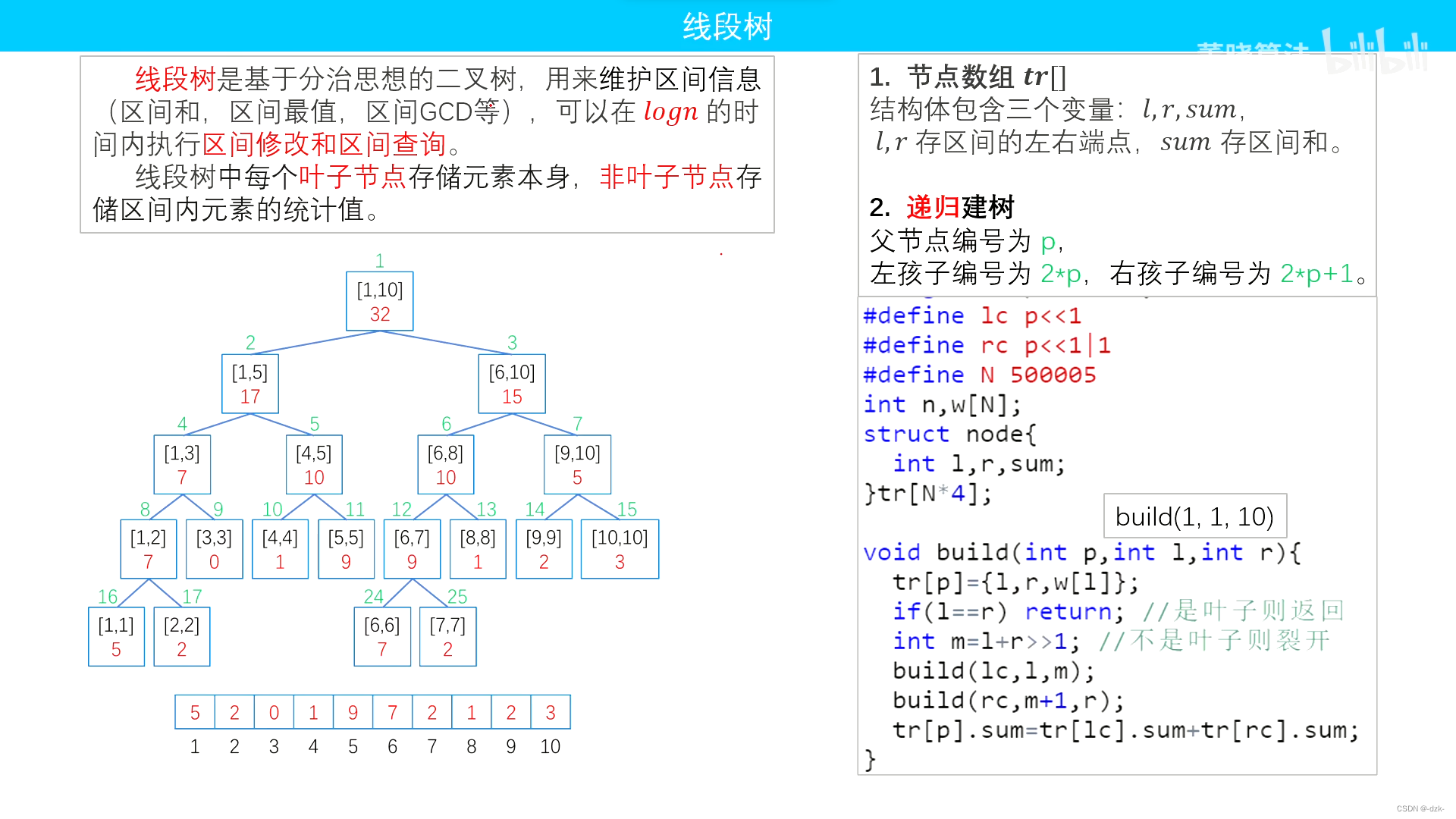
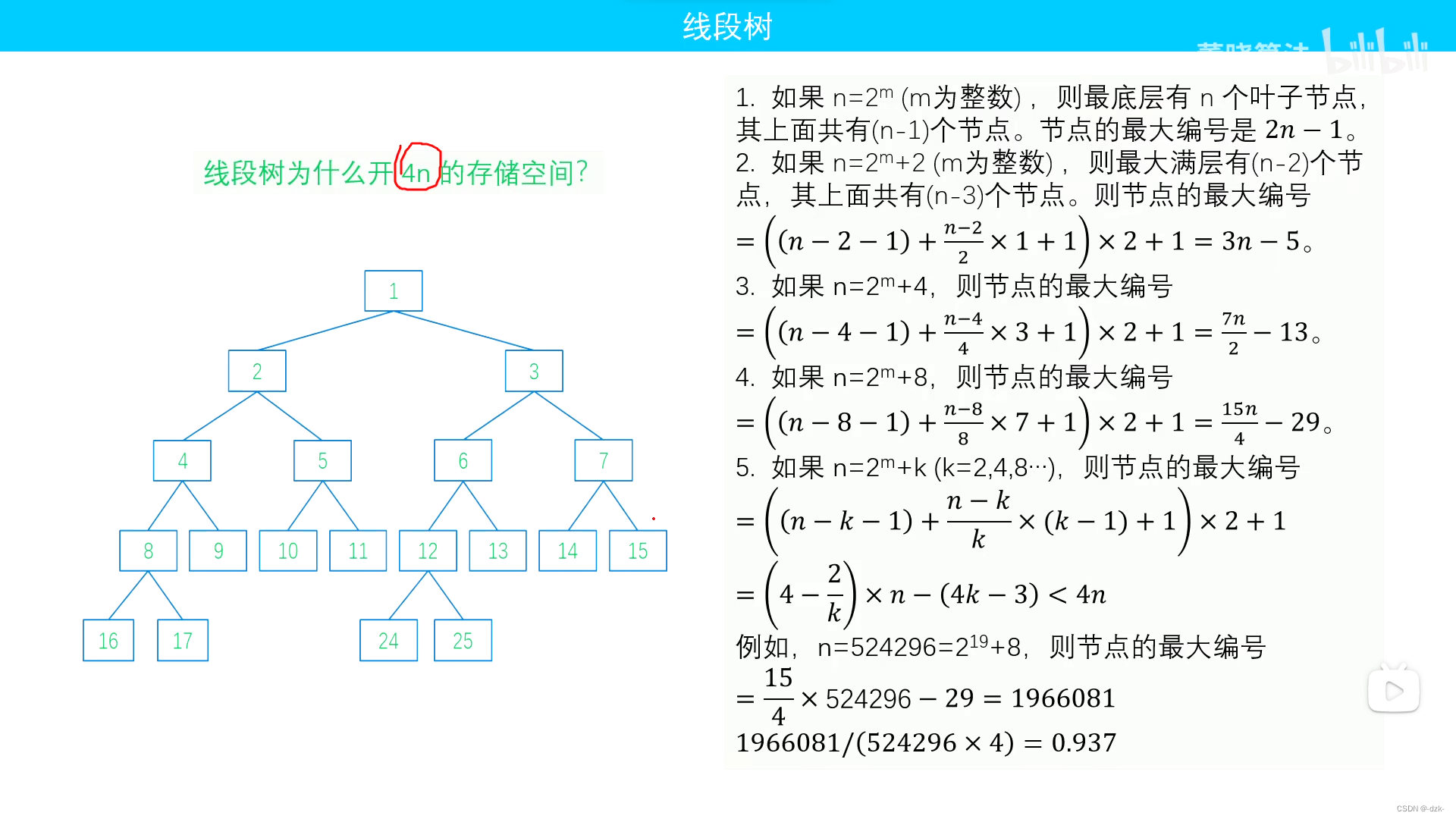
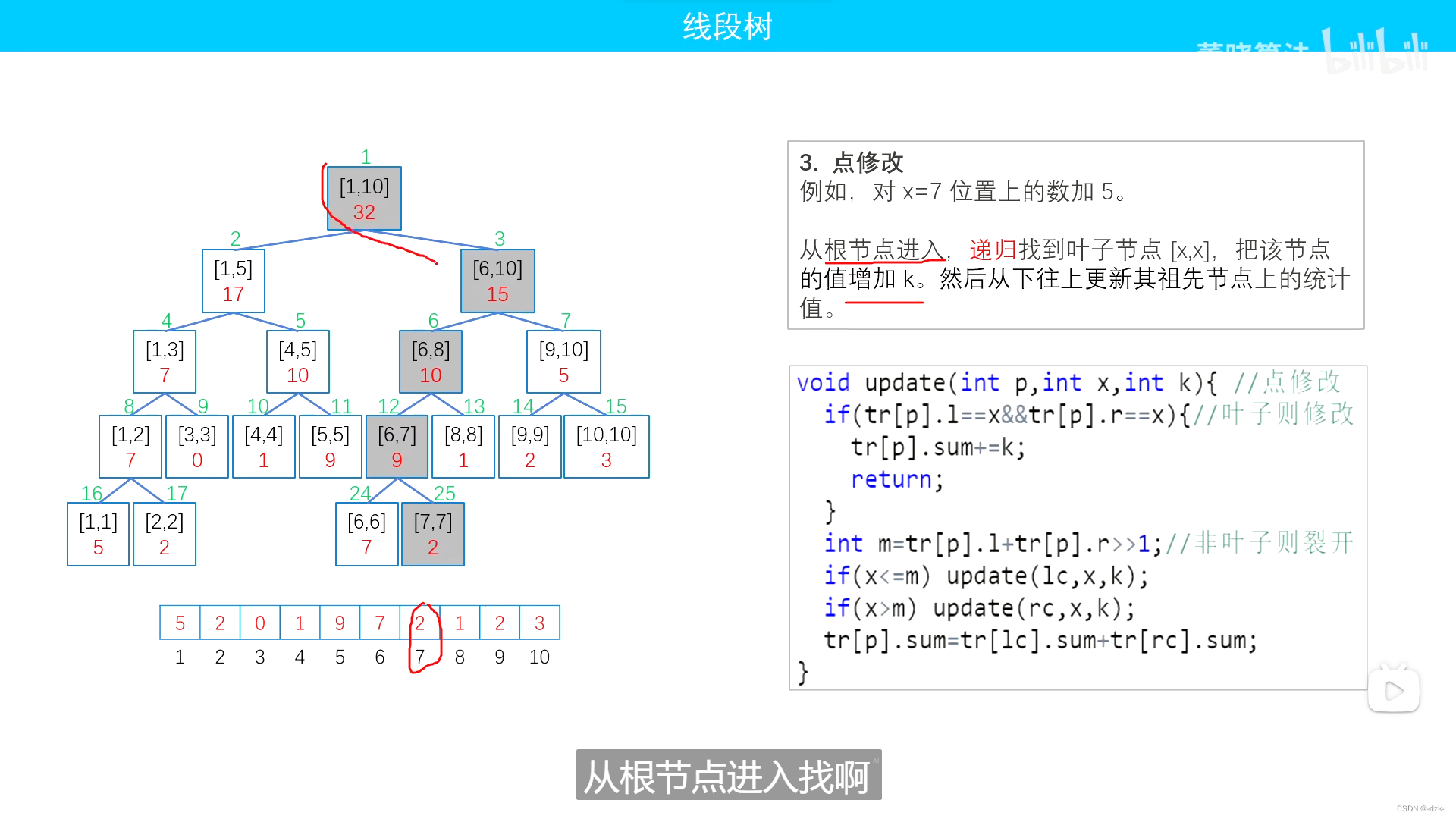
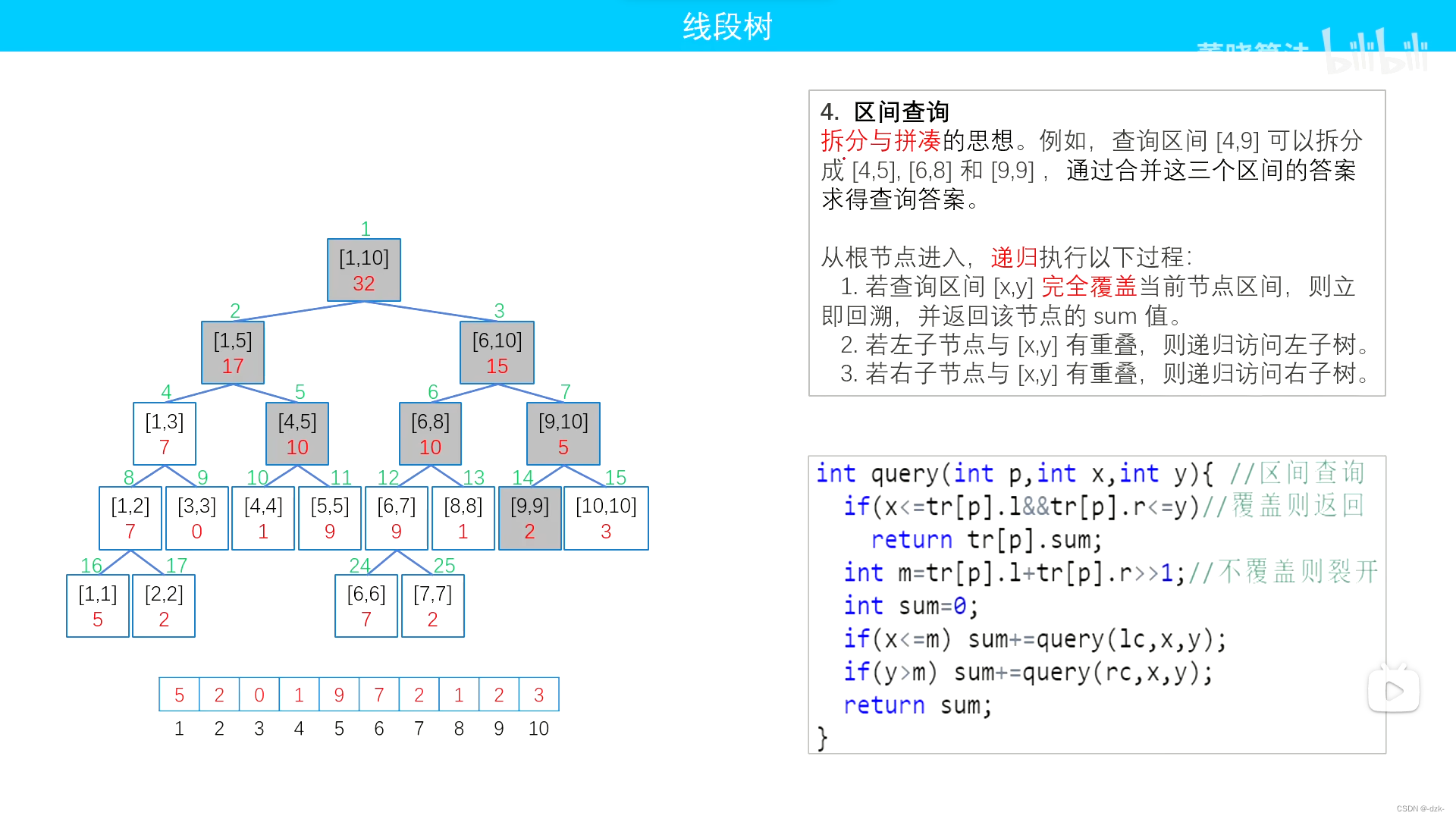
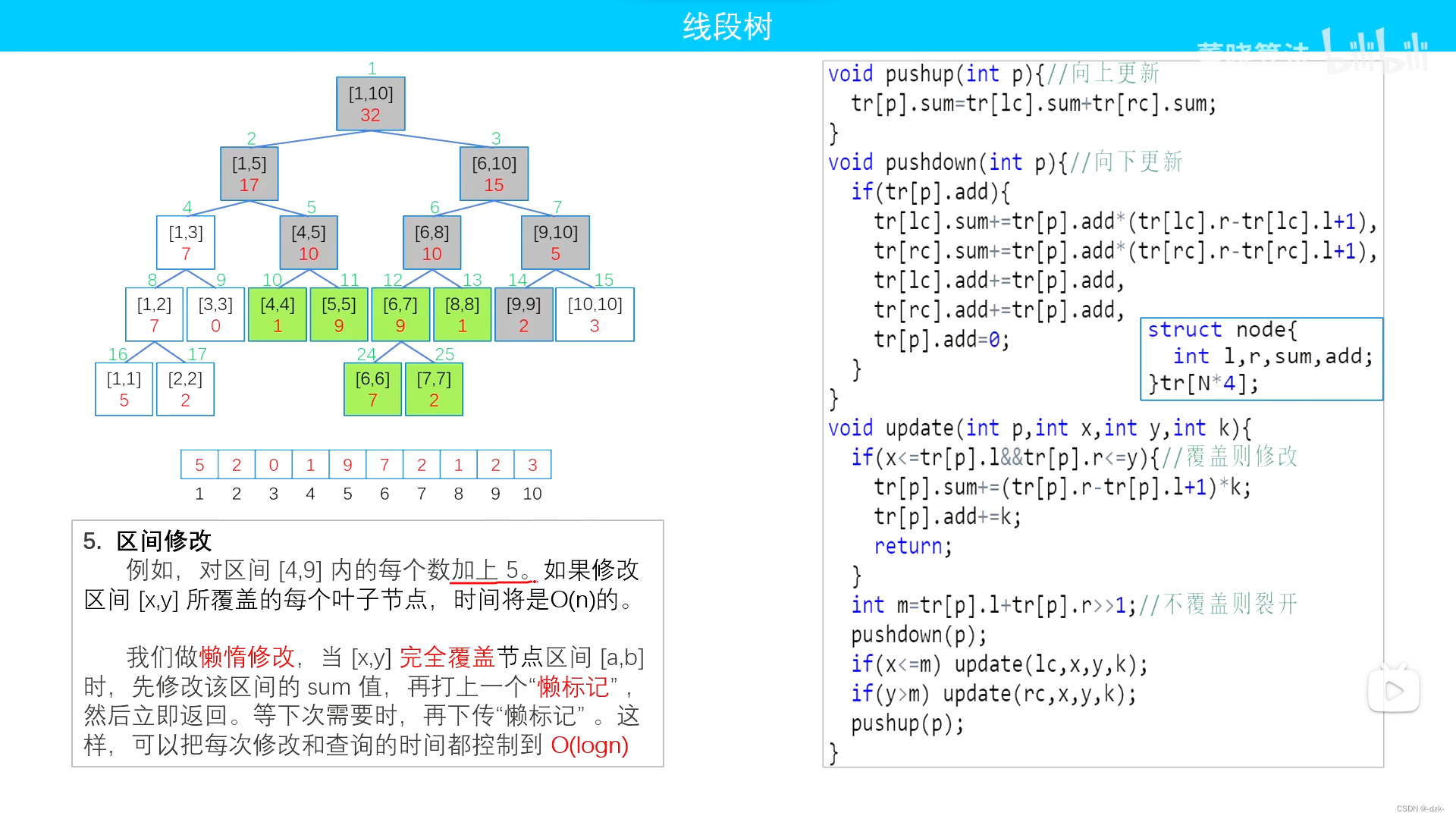

核心模板
#define lc p<<1
#define rc p<<1|1
int n,w[N]; //w[]是需维护的一维数组
struct node{
int l,r,sum,add;
}tr[N*4];
//向上更新
void pushup(int p){
tr[p].sum=tr[lc].sum+tr[rc].sum;
}
//向下更新
void pushdown(int p){
if(tr[p].add){
tr[lc].sum+=tr[p].add*(tr[lc].r-tr[lc].l+1);
tr[rc].sum+=tr[p].add*(tr[rc].r-tr[rc].l+1);
tr[lc].add+=tr[p].add;
tr[rc].add+=tr[p].add;
tr[p].add=0;
}
}
void build(int p,int l,int r){
tr[p]={l,r,w[l],0};
if(l==r) return ; //是叶子则返回
int m=l+r>>1; //不是叶子则裂开
build(lc,l,m);
build(rc,m+1,r);
pushup(p);
}
void update(int p,int x,int y,int k){
if(x<=tr[p].l&&tr[p].r<=y){ //覆盖则修改
tr[p].sum+=(tr[p].r-tr[p].l+1)*k;
tr[p].add+=k;
return ;
}
int m=tr[p].l+tr[p].r>>1; //不覆盖则裂开
pushdown(p);
if(x<=m) update(lc,x,y,k);
if(y>m) update(rc,x,y,k);
pushup(p);
}
int query(int p,int x,int y){
if(x<=tr[p].l&&tr[p].r<=y) return tr[p].sum; //覆盖则返回
int m=tr[p].l+tr[p].r>>1; //不覆盖则裂开
pushdown(p);
int sum=0;
if(x<=m) sum+=query(lc,x,y);
if(y>m) sum+=query(rc,x,y);
return sum;
}