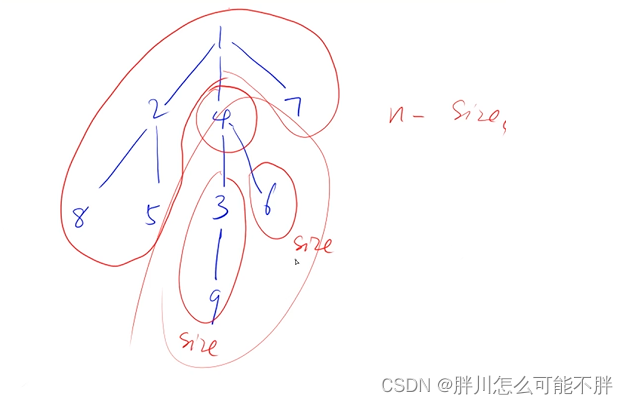
树的重心

 

本题的本质是树的dfs， 每次dfs可以确定以u为重心的最大连通块的节点数，并且更新一下ans。

也就是说，dfs并不直接返回答案，而是在每次更新中迭代一次答案。

这样的套路会经常用到，在 树的dfs 题目中

 

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<cstring>
#include <unordered_set>
//#include<priority_queue>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;

 ll  INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;

const ll N = 2e6+ 10;
const ll mod =998244353;
int t,n,m,x,y,ca;
ll arr[N],brr[N],crr[N];
int h[N],ne[N],e[N],idx;
int ans;
int book[N];

void add(int a, int b)
{
  e[idx] = b,ne[idx] = h[a] ,h[a] = idx++;
}

// dfs 框架
/*
void dfs(int u){
    st[u]=true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(!st[j]) {
            dfs(j);
        }
    }
}
*/

//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u)
{
  int sum = 1;//存储 以u为根的树 的节点数, 包括u，如图中的4号节点
  int res = 0;//存储 删掉某个节点之后，最大的连通子图节点数
  book[u] = 1;
  for(int i = h[u]; i != -1; i = ne[i])
  {
    int j = e[i];
    if(!book[j])
    {
      int s = dfs(j);// u节点的单棵子树节点数
      res = max(res ,s);// 记录最大联通子图的节点数
      sum += s;//以j为根的树 的节点数
    }
  }
  res = max(res ,n - sum); // 选择u节点为重心，最大的 连通子图节点数
  ans = min(ans ,res);//遍历过的假设重心中，最小的最大联通子图的 节点数
  return sum;
}

void fatchuan()
{
  memset(h,-1,sizeof(h));
  ans = INF;
  cin >> n;
  rep(i,2,n)
  {
    int a,b;
    cin >> a >> b;
    add(a,b),add(b,a);
  }
  dfs(1);
  cout << ans;
}



int main()
{
    IOS;
    t=1;
    //scanf("%d",&t);
    //cin>>t;
    ca=1;
    while(t--)
    {
      fatchuan(); 
      ca++;
    }    
    return 0;
}