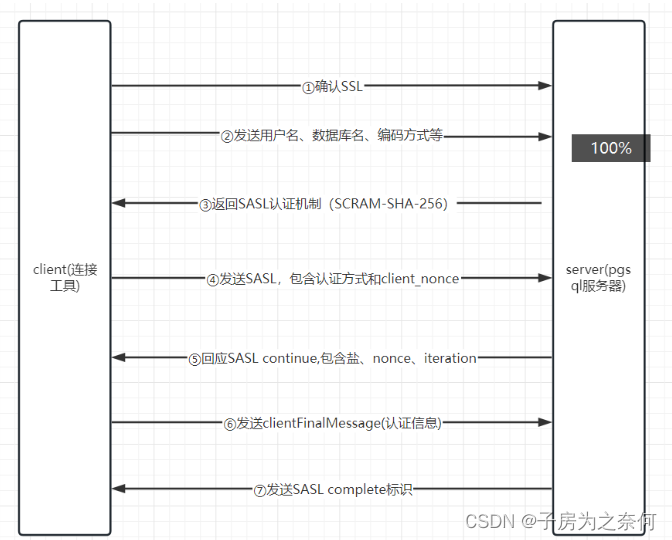
IMU学名惯性测量单元，所有的运动都可以分解为一个直线运动和一个旋转运动，故这个惯性测量单元就是测量这两种运动，直线运动通过加速度计可以测量，旋转运动则通过陀螺。

void IMUupdate(float gx, float gy, float gz, float ax,float ay, float az)
{
    float norm;
    float vx, vy, vz;
    float ex, ey, ez;

    float q0q0 = q0*q0;
    float q0q1 = q0*q1;
    float q0q2 = q0*q2;
    float q1q1 = q1*q1;
    float q1q3 = q1*q3;
    float q2q2 = q2*q2;
    float q2q3 = q2*q3;
    float q3q3 = q3*q3;

    if(ax*ay*az==0)
        return;

    // 第一步：对加速度数据进行归一化
    norm = sqrt(ax*ax + ay*ay + az*az);
    ax = ax / norm;
    ay = ay / norm;
    az = az / norm;



    // 第二步：DCM矩阵旋转

    vx = 2*(q1q3 - q0q2);
    vy = 2*(q0q1 + q2q3);
    vz = q0q0 - q1q1 - q2q2 + q3q3 ;


    // 第三步：在机体坐标系下做向量叉积得到补偿数据

    ex = ay*vz - az*vy ;
    ey = az*vx - ax*vz ;
    ez = ax*vy - ay*vx ;


    // 第四步：对误差进行PI计算，补偿角速度
    exInt = exInt + ex * Ki;
    eyInt = eyInt + ey * Ki;
    ezInt = ezInt + ez * Ki;

    gx = gx + Kp*ex + exInt;
    gy = gy + Kp*ey + eyInt;
    gz = gz + Kp*ez + ezInt;


    // 第五步：按照四元数微分公式进行四元数更新
    q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
    q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
    q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
    q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;

}

​​​​​​​1. 数据规范化

在使用一个算法之前首先要弄清楚数据数据的单位是什么，在互补滤波算法中，角速度的单位是“弧度每秒”，加速度是数据是归一化后的数据，无单位。

2. DCM旋转矩阵

通过旋转矩阵计算标准加速度在当前姿态下的理论加速度分量，其中旋转矩阵通过四元素得到。（四元数，欧拉角，和旋转矩阵之间可以相互转换）。

3. 通过向量叉积得到误差

这个误差指的是两个向量的不平行程度，和夹角的正弦成正比，叉乘=a*b*sin(角度),二两个向量又归一化了，所以就和sin(角度成正比)，进而反应了陀螺仪估计的姿态和加速度计测量的姿态误差。Mahony那篇论文用叉乘来表示误差是有其物理意义的。一般来说向量的误差不是用叉乘来表示，直接作减法会更合适。而单位向量的向量叉积在物理意义上在小角度意义就是轴角，轴角本身就刻画了旋转，也就是叉乘的结果可以看成是旋转误差，在这个物理意义下比任何误差表示都要合理和切合实际系统。

4. PID调节

5. 四元素微分公式

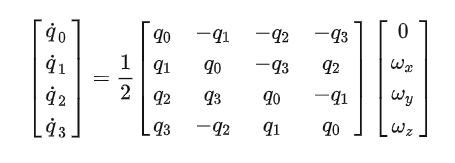
利用PID补偿后的角速度对四元数进行更新。