1. 旋转矩阵

 1.1 点、向量和坐标系

点：点是空间中的基本元素，没有长度，没有体积；

向量：把两个点连接起来，就构成了向量，向量可以看成从某点指向另一点的一个箭头；只有当我们指定这个三维空间中的某个坐标系时，才可以谈论该向量在此坐标系下的坐标；默认向量就是列向量；
坐标系：三根不共面的轴，坐标系的三根坐标轴的方向向量就是基，坐标系能用它的基来表示；

标准正交基：两两正交、单位长度（基就是张成这个空间的一组线性无关的向量。
 

任意向量在基下的坐标（坐标 + 坐标系可以表示向量）。

机器人中有各种各样的坐标系

• 世界系 World、机体系 Body、传感器参考系 Sensor

向量点乘和叉乘

点乘（内积）：结果是一个数

叉乘（外积）：结果是一个向量，方向垂直于这两个向量，大小为 |a||b|sin<a,b>

通过上述等式，我们引入符号^，把 写成矩阵， 实际上是一个反对称矩阵，可以把写成矩阵与向量的乘法 ，变成线性运 算。此符号是一个一一映射，意味着任意向量都对应着唯一的一个反对称矩阵，反之亦然:

2. 坐标系间的欧式变换

2.1 欧式变换之旋转

 

 

 

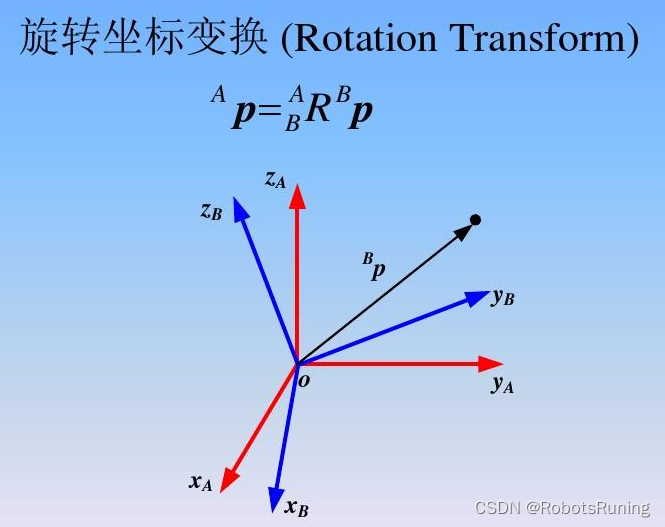
1. 两个坐标系间的欧式变换

        我们经常在实际场景中定义各种各样的坐标系，如果考虑运动的机器人(即相机)，那么常见的做法是设定一个惯性坐标系(或者叫世界坐标系)，可以认为它是固定不动的。

        刚体运动： 两个坐标系之间的运动变换由一个旋转加上一个平移组成，这种运动就是刚体运动。相机运动就是一个刚体运动。刚体运动过程中，同一个向量在各个坐标系下的长度和夹角都不会发生变化。此时，我们说手机坐标系和世界坐标系之间，相差了一个欧氏变换(Euclidean Transform)。

旋转矩阵也有一些特别的性质，我们通过矩阵R的行列式可以看出，它是一个行列式为1的正交矩阵。反过来说，行列式为1的正交矩阵也是一个旋转矩阵
 

视觉SLAM十四讲 3-三维空间刚体运动_三维空间中的刚体有哪几个运动维度组成_Nismilesucc的博客-CSDN博客

视觉SLAM十四讲笔记-第三讲 刚体运动_独自悠哉独自在的博客-CSDN博客