机器学习-方差和偏差理论

关于机器学习方差和偏差的内容其实很重要，这个方差和偏差可以帮助我们去分析，模型的泛化能力和过拟合的程度。
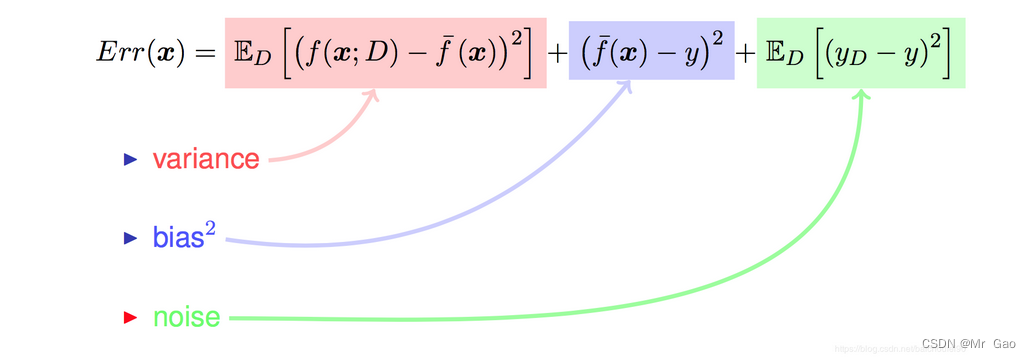
下面我们先给存储方差和偏差的公式：
注意，下式当中，$f(x;D)表示在数据集D上训练出的模型，f^{-}(x)表示无穷多个不同数据集训练出的加权平均模型，y表示假设中的最优模型。$

注：下面说的不同数据集，实质上是同源的，也就是本质上来源于一个性质的数据源。

其实我们从上式可以看出，方差就是不同数据集训练出的模型内方差。

偏差就是不同数据集训练出的模型，在对其计算平均模型，平均模型与最优模型的平方差就是偏差。

如果你有着很多的机器学习实战，或许，你可以推导出，泛化能力、过拟合程度和方差与偏差的联系。

下面博主就总结一下，泛化能力、过拟合程度和方差与偏差的联系：
（1）很显然，方差越大，说明在不同数据集上的参数差异大，即模型差异大，也就是模型对于数据集过于敏感，也就是过拟合的可能性越大，所以，方差越大模型越可能过拟合。
（2)那么偏差呢？偏差越大说明模型和最优模型的结果差异越大，也就是模型效果不好，即泛化能力越差。
所以理想状态下，我们希望，方差和偏差都比较小，这是最好的。

对于方差和偏差的实验应该也是挺有趣的，但是时间有限，博主就不做了，不过我知道怎么做这个实验，感兴趣的同学可以咨询我啊。