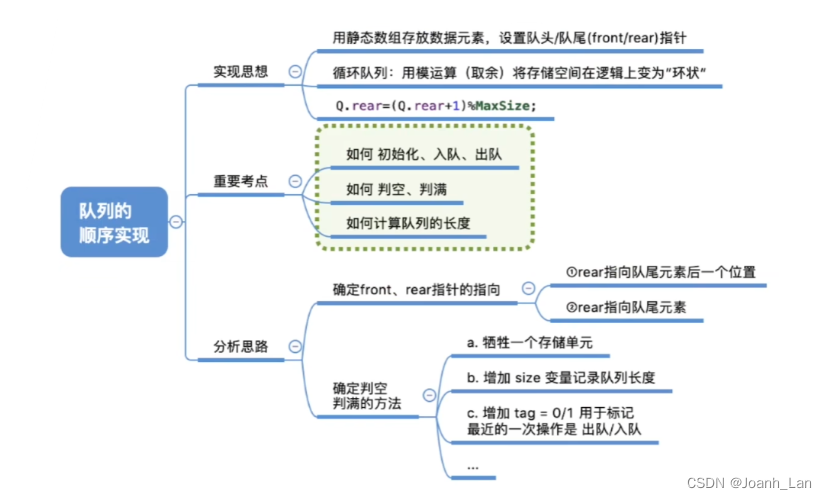
数据结构–队列的顺序实现

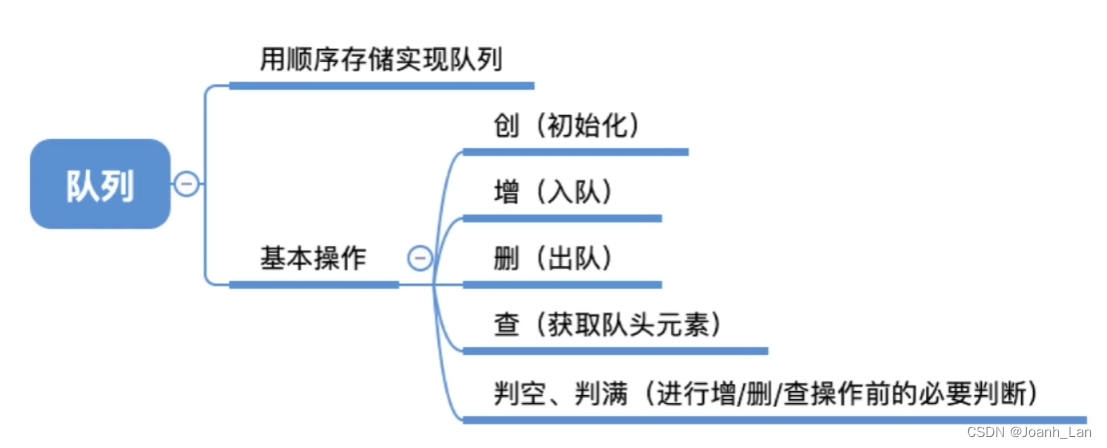
队列的顺序存储代码定义

#define MaxSize 10 //定义队列中元素最大个数
typedef struct
{
    ElemType data[MaxSize]; //静态数组存放队列元素
    int front, rear; //对头指针 & 队尾指针
} SqQueue;	

初始化操作

void InitQueue(SqQueue &Q)
{
    Q.rear = Q.front = 0;
}

判断队列是否为空

bool QueueEmpty(SqQueue Q)
{
    return Q.rear == Q.front;
}

入队操作

bool EnQueue(SqQueue &Q, ElemType x)
{
    if (队列已满)   return false;

    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1) % MaxSize;
    return true;
}

用模运算将存储空间在逻辑上变成了
$“环状”$

这样可以$节约空间$

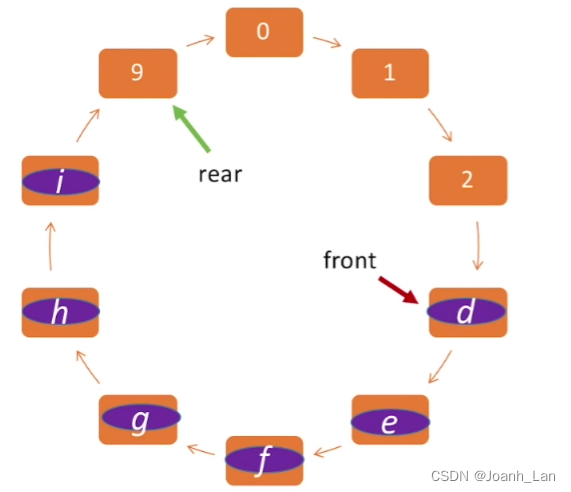
入队代码就变成这个：

bool EnQueue(SqQueue &Q, ElemType x)
{
    if ((Q.rear + 1) % MaxSize == Q.front)   return false;

    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1) % MaxSize;
    return true;
}

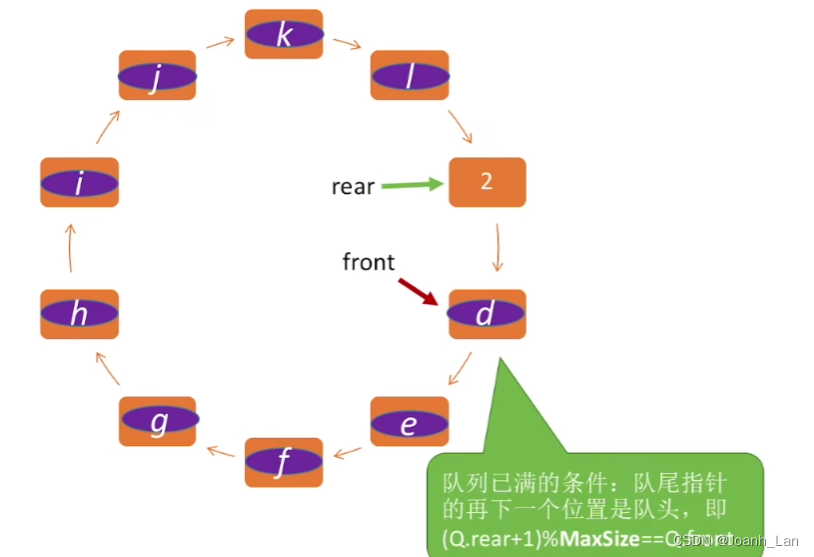
我们可以发现这种逻辑会牺牲一个存储空间

解决方法：
方法一：引进队列元素个数

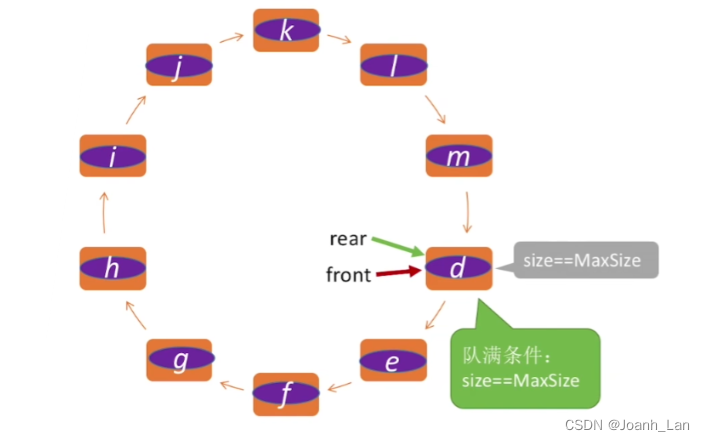
方法二：

记录上一次操作是插入 or 删除

只有删除操作，才可能导致队空
只有插入操作，才可能导致队满

出队操作

bool DeQueue(SqQueue &Q, ElemType &x)
{
    if (Q.rear == Q.rear)   return false;
    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}

获取队头元素

bool GetHead(SqQueue Q, ElemType &x)
{
    if(Q.rear == Q.front)   return false;
    x = Q.data[Q.front];
    return true;
}

ps：要根据实际的逻辑来书写代码，注意是否需要保证 不牺牲存储空间

知识点回顾与重要考点