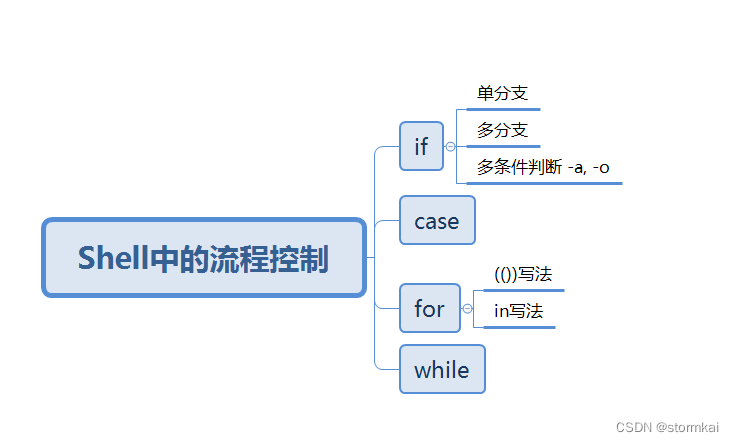
文章目录
-
- 概要
- 整体架构流程
- 技术名词解释
- 技术细节
- 小结
概要
提示:这里可以添加技术概要
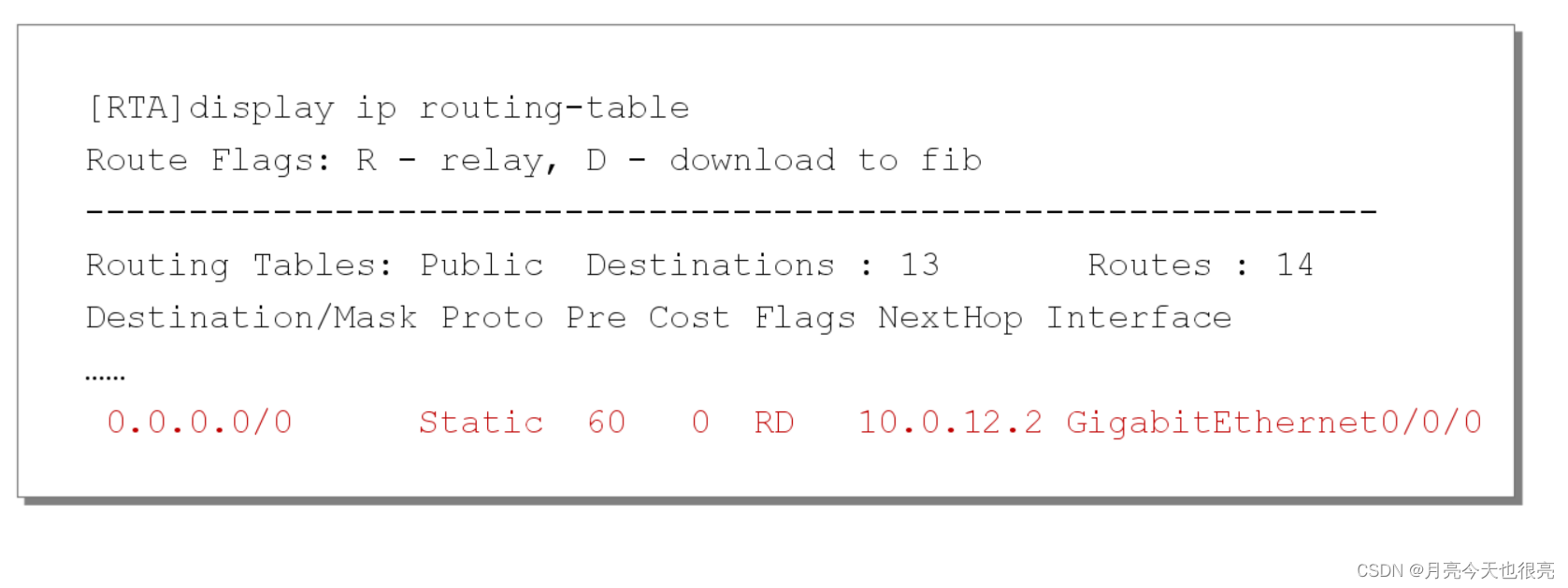
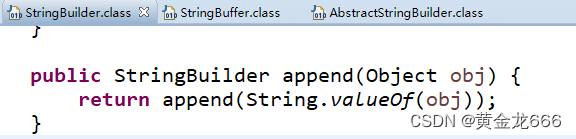
接 触 ADC 或 DAC 时您一定会碰到这个经常被引用的公式,用于计算转换器理论信噪 比(SNR)。与其盲目地相信表象,不如从根本上了解其来源,因为该公式蕴含着一些微 妙之处,如果不深入探究,可能导致对数据手册技术规格和转换器性能的误解。记住, 该公式代表的是完美 N 位 ADC 的理论性能。您可以比较 ADC 的实际 SNR 与理论 SNR, 看看二者有何异同。
整体架构流程
提示:这里可以添加技术整体架构
理想转换器对信号进行数字化时,最大误差为±½LSB,如图 1 的一个理想 N 位 ADC 的 传递函数所示。对于任何横跨数个 LSB 的交流信号,其量化误差可以通过一个峰峰值 幅度为 q(一个 LSB 的权重)的非相关锯齿波形来近似计算。对该近似法还可以从另 一个角度来看待,即实际量化误差发生在±½q 范围内任意一点的概率相等。虽然这种 分析不是百分之百精确,但对大多数应用是足够准确的
技术名词解释
提示:这里可以添加技术名词解释
例如:
- Bert
- GPT 初代
- GPT-2
- GPT-3
- ChatGPT
技术细节
提示:这里可以添加技术细节
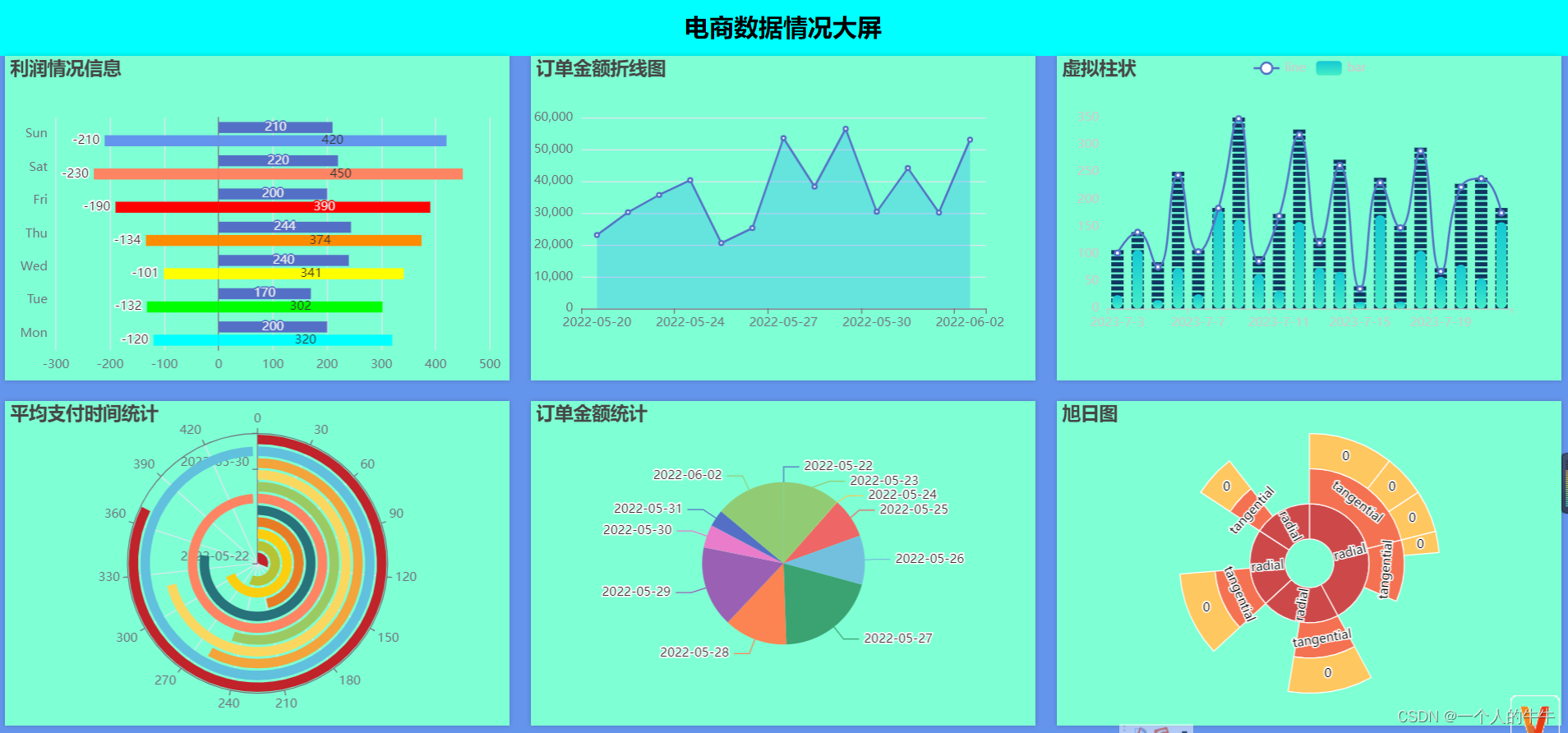
贝尔实验室的 W.R.Bennett1948 年发表的经典论文中,分析了量化噪声的实际频谱。 采用上述简化假设,他的详细数学分析可以简化为图 1 所示。继 Bennett 的经典论文 之后,还有其它一些关于转换器噪声的重要论文和著作。 图 2 更详细地显示了量化误差与输入电压的关系。同样,一个简单的锯齿波形就能提 供足够准确的分析模型。锯齿误差的计算公式如下:

因此,均方根量化误差为:

锯齿误差波形产生的谐波远远超过 DC 至 fs/2 的奈奎斯特带宽,然而,所有这些高阶 谐波必须折回(混叠)到奈奎斯特带宽并相加,产生 q/√12 的均方根噪声。 正如 Bennett 所指出的,量化噪声近似于高斯分布,几乎均匀地分布于从 DC 至 fs/2 的奈奎斯特带宽。这里假设量化噪声与输入信号不相关。在某些条件下,当采样时钟 ,量化噪声与时间的关系 MT 和信号通过谐波相关时, 量化噪声将与输入信号相关,能量集中在信号的谐波中,但均方根值仍然约为 q/√12。 理论信噪比现在可以通过一个满量程输入正弦波来计算
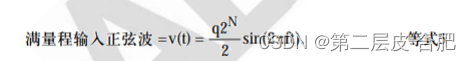

Bennett 论文说明:虽然量化噪声的实际频谱相当复杂,难以分析,但推导出等式 9 的简化分析对大多数应用足够准确。然而,必须再次强调,均方根量化噪声是在 DC 至 fs/2 的完整奈奎斯特带宽范围内进行测量 .
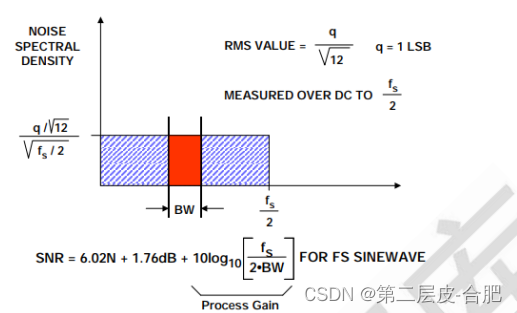
许多应用中,实际目标信号占用的带宽 BW 小于奈奎斯特带宽(参见图 3)。如果使 用数字滤波来滤除带宽 BW 以外的噪声成分,则等式中必须包括一个校正系数(称为 “处理增益”),以反映 SNR 的最终提高,如等式 10 所示。

以两倍以上的信号带宽的速率对信号进行采样的过程称为“过采样”。过采样、量化 噪声整形和数字滤波均是 Σ-Δ 型转换器的重要概念,不过任何 ADC 架构都可以采用过 采样技术
处理增益的意义可以通过下例说明。在许多数字基站或其它宽带接收机中,信号带宽 由许多独立的通道组成,一个 ADC 对整个带宽进行数字化处理。例如,美国的模拟蜂 窝无线电系统(AMPS)由 416 个 30kHz 带宽通道组成,占用的带宽约为 12.5MHz。假设 采样速率为 65MSPS,并且使用数字滤波来分离各个 30kHz 通道。在这些条件下,过 采样导致的处理增益为
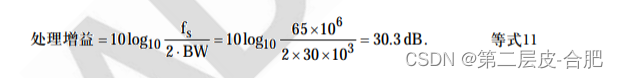
总结
例如:
将处理增益加入 ADC SNR 规格,便得到 30kHz 带宽内的 SNR。上例中,如果 ADC SNR 规格为 65dB(DC 至 fs/2),则 30kHz 通道带宽内的 SNR 提高到 95.3dB(经过适当 的数字滤波后)。