基于灰狼优化算法的最小二乘支持向量机及其MATLAB实现

在这里插入图片描述

常用的预测方法有回归分析法、神经网络法、支持向量机(SVM, Support Vector Machine)等。回归分析法是建立影响因素与目标量之间的回归方程，建模过程简单，但预测精度较低。神经网络法适合分析大量非线性数据样本，挖掘其潜在规律，具有良好的非线性映射与泛化能力，但网络训练速度慢且易陷入局部极小值。支持向量机是基于结构风险最小化原则，可以避免易陷入局部最优解，适合解决小样本、高维度问题。其中，最小二乘支持向量机[1] (LSSVM,Least Squares Support Vector Machine) 是标准支持向量机的扩展，将 SVM 解决的凸二次规划问题转化为求解线性方程组，将非等式约束用等式约束替代，可以降低运算复杂度。但LSSVM 中的正则化系数和核宽度系数的选择对其预测精度有较大的影响，目前依据人工经验确定其值，无法保证模型精度及稳定性。因此，需要寻求一种优化算法自适应来确定最优参数。

在众多的群智能优化算法中，GWO(GWO, Grey Wolf Optimization )算法有着结构简单、需要调节的参数少、容易实现等特点[2]，在参数优化领域展现出卓越的性能。

综上，本文将运用灰狼算法对最小二乘支持向量机的参数进行优化，同时，为验证算法的有效性，引入网格搜索的LSSVM、遗传算法(,GA ,Genetic Algorithm)优化的最小二乘支持向量机以及BP神经网络，最后证明了最小二乘支持向量机在该问题上性能优于BP神经网络，且GWO-LSSVM也优于GA-LSSVM.

00目录

1 最小二乘支持向量机模型
2 灰狼优化算法
3 GWO-LSSVM预测模型
4 代码目录
5 仿真
6 源码获取

01 最小二乘支持向量机模型

基于SVM的思想，Suykens等人提出了最小二乘支持向量机。将SVM中复杂的二次规划问题转变为求解线性方程，因此LSSVM相较于SVM极大提升了计算效率。其具体原理和数学推导如下。

假设样本数据集为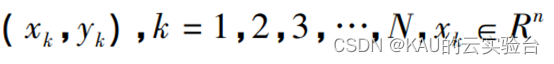：在这里插入图片描述

LSSVM 的关键是将训练和样本通过非线性映射反映到高维特征空间，在高维空间中进行线性回归,回归函数描述如下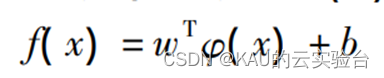：在这里插入图片描述

式中，ｗ为权重向量；φ(x)为投影函数；ｂ为阈值。将回归等式转化为最小化代价函数约束的优化问题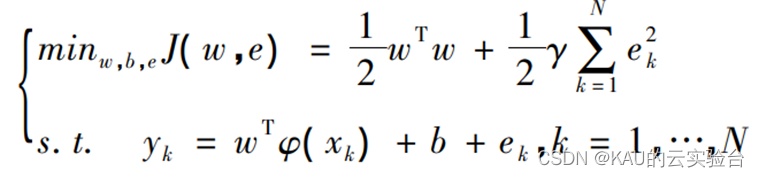：在这里插入图片描述

式中，γ为正则化参数，作用为平衡模型的复杂性和精度；ek为输入向量的训练误差。与SVM不同的是，LSSVM使用等式约束而非不等式约束。基于上述等式,为寻找目标函数最小值，对上式引入拉格朗日乘子，即：
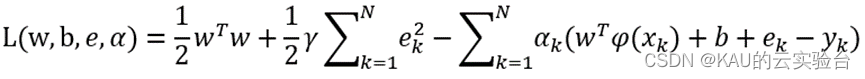
在这里插入图片描述

根据KKT条件，对其求解可得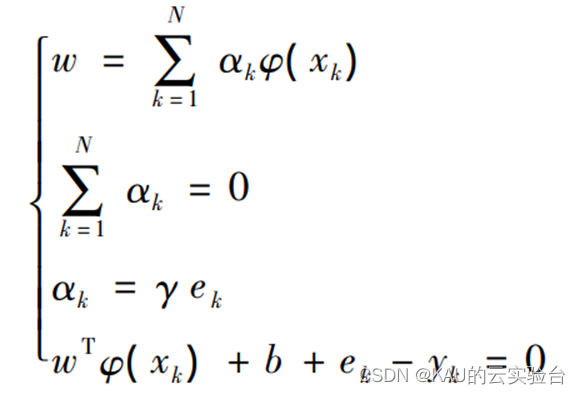：在这里插入图片描述

消去w和ek，得到模型预测函数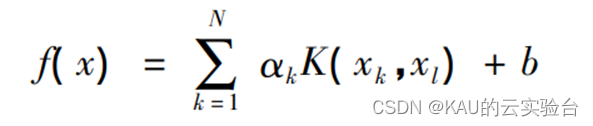：在这里插入图片描述

式中：K(…)为核函数，表示低维空间到高维空间的映射关系。本文采用径向基核函数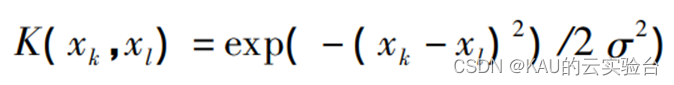：在这里插入图片描述

其中，σ 表示核函数宽度。

在 LSSVM 模型中，惩罚因子 g 控制模型对误差的惩罚程度，直接影响模型的泛化能力，s 反映训练参数的分布。这两个参数的取值直接影响了预测效果。因此，建立 LSSVM 模型时有必要选择智能算法对这两个参数进行优化。

02 灰狼优化算法

LSSVM的2个参数主要是依靠经验自行设定，难以使模型获得较佳的性能，虽然后续也发展了网格搜索法寻优，但没有摆脱传统算法的弊端，需要遍历所有组合，计算量庞大、耗费时间长且精准度不高，于是逐渐衍生出使用群智能优化算法全局优化参数的方法。

灰狼优化算法是2014年由澳大利亚学者Mirjalili等提出的一种群智能优化算法。GWO算法模拟自然界中灰狼种群等级机制和捕猎行为。通过4种类型的灰狼(𝛼，𝛽，𝛿，𝜔)来模拟社会等级。通过狼群跟踪﹑包围、追捕、攻击猎物等过程来模拟狼的捕猎行为,实现优化搜索目的。GWO算法具有原理简单、并行性﹑易于实现,需调整的参数少且不需要问题的梯度信息,有较强的全局搜索能力等特点。

在函数优化方面, Mirjalili等通过对29个基准函数的测试表明,GWO算法在求解精度和收敛性方面明显优于粒子群优化(PSO)、重力搜索算法(GSA),差分进化(DE),进化规划(EP)和进化策略(ES)的结果。

在GWO算法中, 首先是在搜索空间中随机产生灰狼族群，为构建灰狼的社会等级制度模型,将种群中适应度值最优的解、次优的解和第三优的解分别看作α狼、β狼和𝛿狼,而剩余的解被视为𝜔狼。然后由α狼、β狼和𝛿狼来负责引导, 𝜔狼则跟随着α狼、β狼和𝛿狼,通过搜寻猎物﹑包围猎物和攻击猎物来完成狩猎优化，最终获取最优解。

2.1 社会等级

设计GWO算法时,狼群中每一个灰狼代表了种群的一个潜在解,为了描述灰狼的社会等级﹐将α狼的位置视为最优解﹔将β和𝛿狼的位置分别作为优解和次优解; 𝜔狼的位置作为其余的候选解。在GWO算法中,由a , β和𝛿引导搜索(优化),而𝜔狼跟随前面3种狼。

2.2 包围猎物

捕猎过程中，灰狼群体会先包围猎物，该行为的数学模型可以表示为:

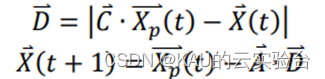
在这里插入图片描述

其中，𝑡代表当前迭代的次数，𝑋𝑝 (𝑡)为第𝑡次迭代中猎物的位置向量，𝑋 (𝑡)为第𝑡次迭代中灰狼的位置向量。𝐴和𝐶为协同向量，计算方式为

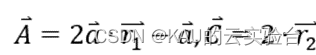
在这里插入图片描述

其中𝑎中的分量在迭代过程中从2到0线性递减，𝑟⃑1 和𝑟⃑2 为[0,1]中的随机向量

2.3 狩猎

灰狼有能力识别猎物的位置并包围它们。狩猎通常由α狼引导, β和𝛿也可能偶尔参与狩猎。然而,在一个抽象搜索空间中,灰狼并不知道最优解(猎物)的精确位置。为了模拟灰狼的狩猎行为,假设α(最优候选解)、β和𝛿拥有更多关于猎物潜在位置的知识。因此,在每次迭代过程中,保存迄今为止获得的3个最优解,迫使其他狼(包括𝜔)根据最优搜索的位置采用以下公式更新它们的位置: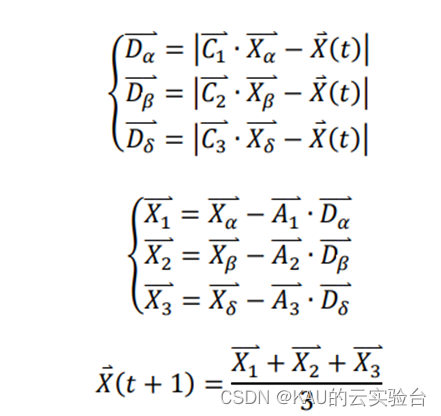 在这里插入图片描述

其中𝑋𝛼 ⃑，𝑋𝛽 ⃑，𝑋𝛿 ⃑ 代表当前迭代中𝛼，𝛽，𝛿的位置向量，𝑋 (𝑡)为第𝑡次迭代中个体的位置向量，𝐶1 ⃑ ，𝐶2 ⃑ ，𝐶3 ⃑ 为随机向量，𝐷𝛼 ⃑，𝐷𝛽 ⃑， 𝐷𝛿 ⃑代表群体中其他个体与𝛼，𝛽，𝛿之间的距离，𝑋 (𝑡 + 1)为个体更新后的位置向量。

下图给出𝜔狼或其他狼(候选狼)如何根据二维搜索空间中的𝛼，𝛽，𝛿狼来更新其位置。从中可以看出,最终位置将在搜索空间中由𝛼，𝛽，𝛿狼的位置定义的圆内的随机位置。换句话说, 𝛼，𝛽，𝛿狼估计猎物的位置,其他狼围绕猎物随机更新它们的位置。

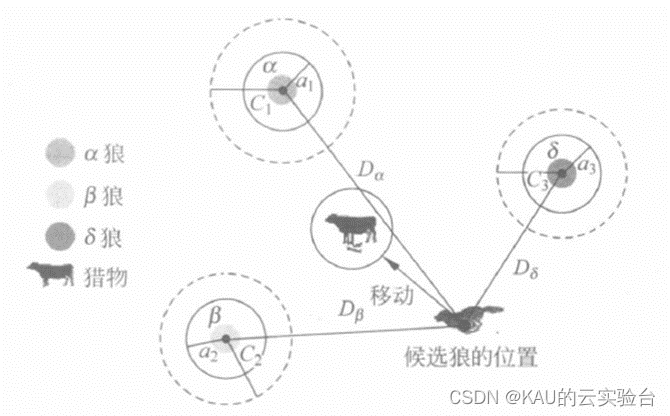
在这里插入图片描述

图源于智能优化计算与涌现计算

2.4 攻击猎物

灰狼在猎物停止移动时通过攻击猎物来完成捕猎。攻击猎物确定猎物位置，即得到最优解，这一过程主要通过迭代过程中收敛因子𝑎 从 2 到 0 的递减来实现，于是群体在迭代结束后，获取最优解。
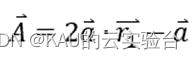
在这里插入图片描述

在 GWO 算法中，通过 a 值逐渐线性减少，使得 A的波动范围也随之线性减少，从而模拟狼群逼近猎物的行为。C 是［0，2］之间随机值，C表示狼所在位置对猎物影响的随机权重，由于C值是一个随机值，用于防止算法寻优时无法摆脱局部最优，对搜寻全局最优解发挥了非常重要的作用，增强了算法的全局搜索能力、鲁棒性与收敛性。

2.5 优化过程

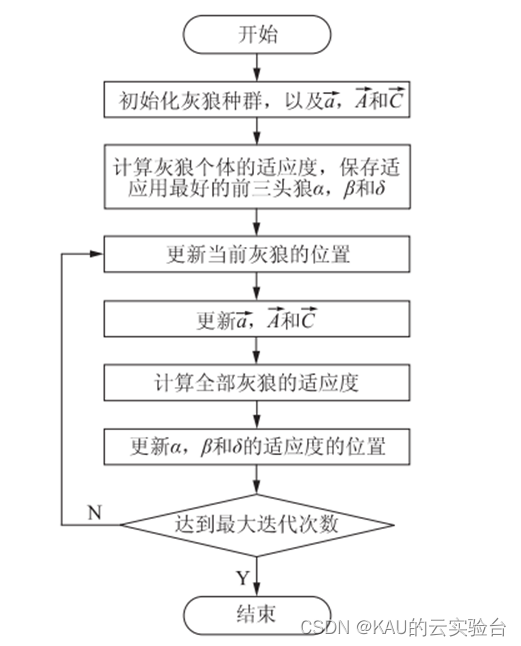
GWO 算法优化流程为首先创建一个灰狼种群，然后在迭代过程中将最优的三个解定义为 α、β 和 δ，而后其他个体根据 α、β 和 δ 的位置判断猎物所在位置，从而更新自己的位置。GWO 算法的流程如图所示
在这里插入图片描述

3 GWO-LSSVM预测模型

传统 LSSVM 模型中的正则化系数和核宽度系数均是根据经验得到的，容易造成模型稳定性差，预测效果不理想。灰狼算法具有全局搜索能力，可以实现自动对 LSSVM 中参数优化选取，有效避免人工选择的盲目性。LSSVM模型需要优化的参数有核函数宽度σ、惩罚因子g，将训练集的RMSE作为适应度函数来优化LSSVM的参数，RMSE的计算方式如下：

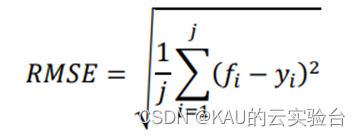
在这里插入图片描述

其中，𝑓𝑖表示第𝑖个样本的预测值，𝑦𝑖表示第𝑖个样本的真实值，𝑗表示样本个数。

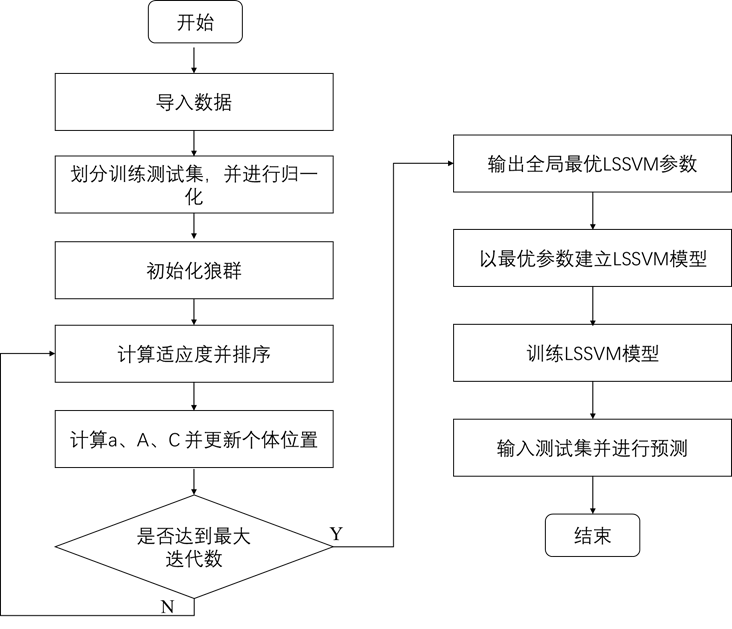
GWO-LSSVM模型的算法流程图如下所示

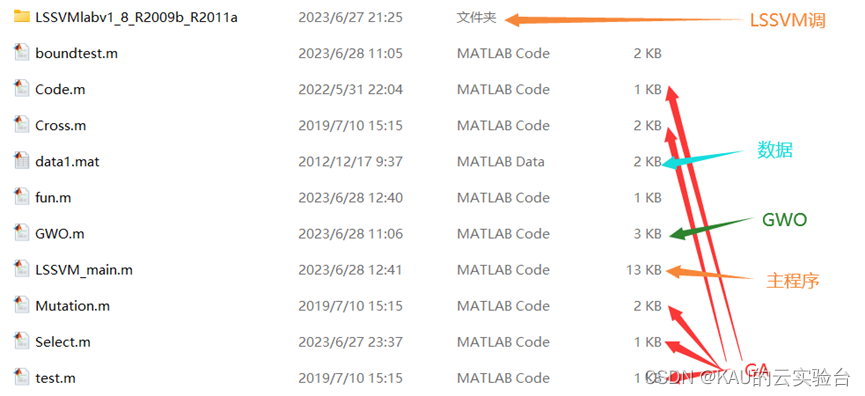
在这里插入图片描述

04 代码目录

在这里插入图片描述

05 仿真

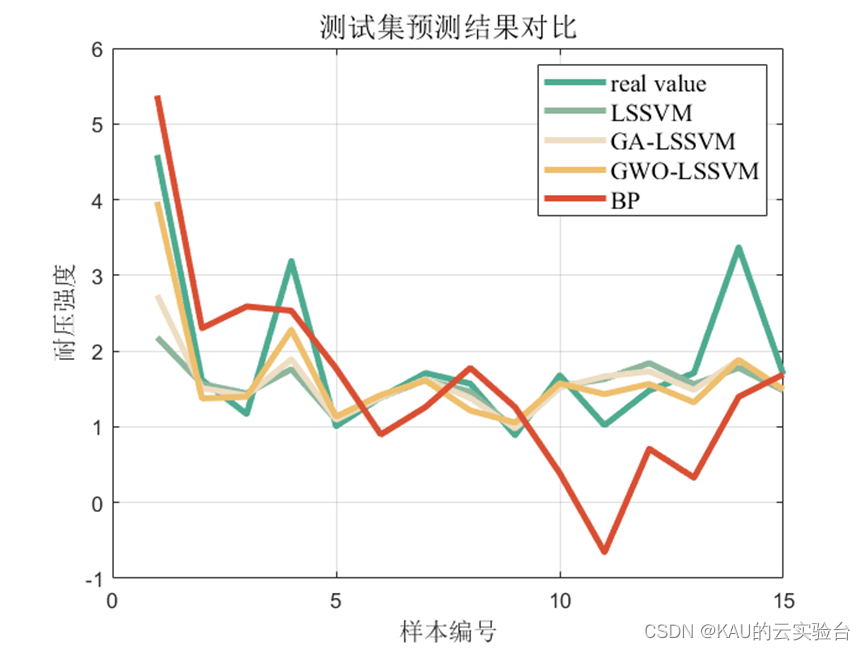
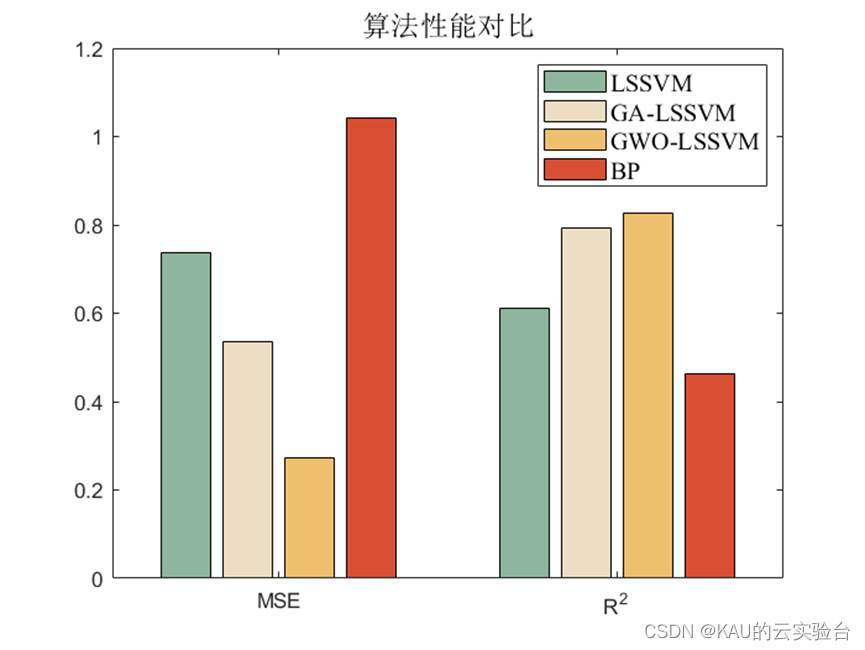
仿真采用的数据是6输入，1输出，样本数量55，取40个作为训练集，15个作为测试集，除GWO-LSSVM外，引入网格搜索的LSSVM、GA-LSSVM、BP神经网络进行对比，结果如下：

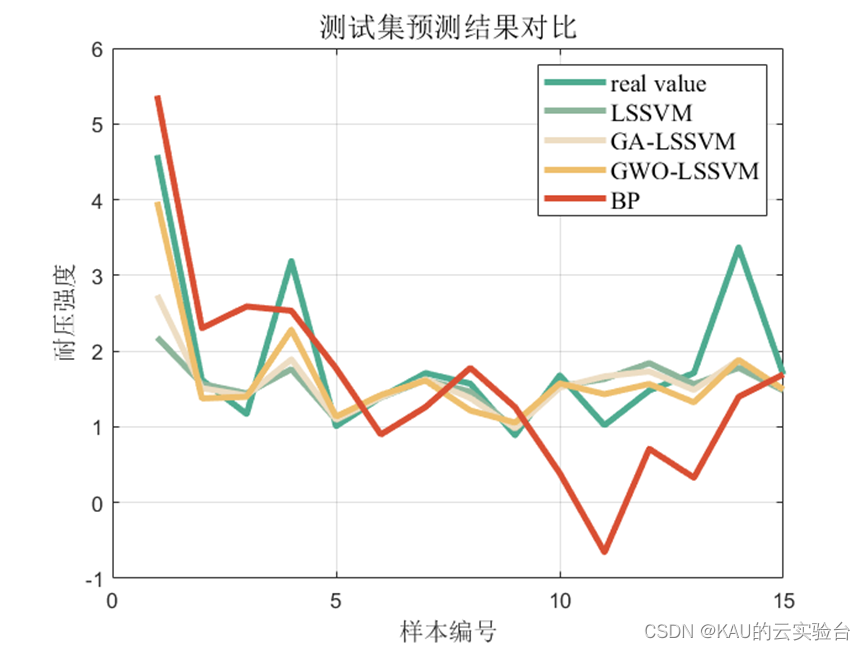
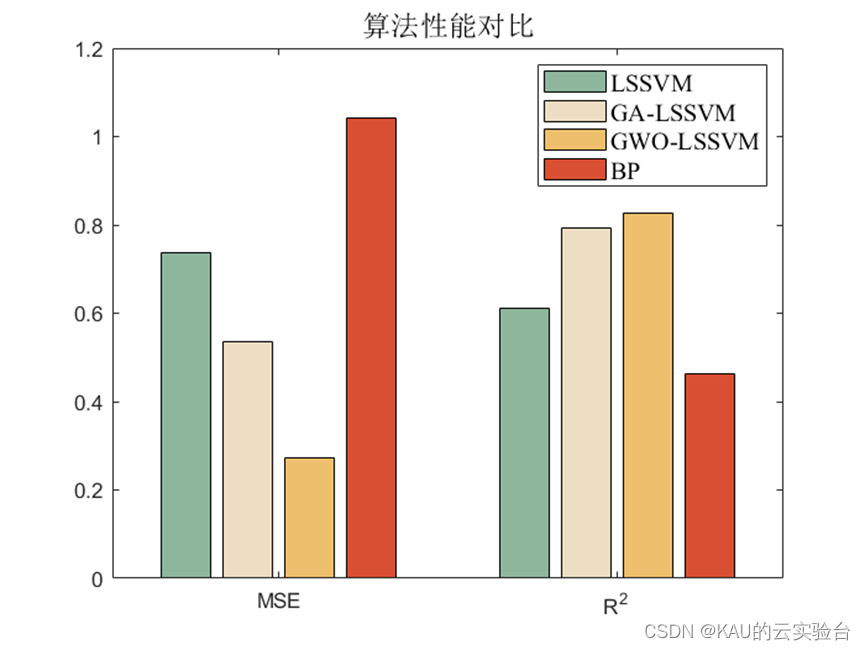
在这里插入图片描述

首先，在该数据集上， LSSVM较之BP神经网络误差更小，拟合程度更好，因此LSSVM具有一定优越性，同时，对比LSSVM,GA-LSSVM与GWO-LSSVM，可以看到GWO-LSSVM数据最佳，也证明了该优化算法的优良效果。

06 源码获取

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
https://mbd.pub/o/bread/ZJqbk5pu
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

参考文献

[1]Suykens J, Lukas L, Van P, et al. Least squares support vector machine classifiers: a large scale algorithm[J], 2000.

[2]张晓凤, 王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(03): 30-8.