前言

相信使用过光盘的读者都会有这样一种经历,如果不小心刮花了盘面,大部分情况下,把它放进DVD机器却仍然可以播放视频,这是为什么呢?

因为光盘的存储原理是同一份内容(二进制)存储三份,当进行播放的时候,会对三份内容进行位校验,按照少数服从多数原则进行 查错或者校订

什么意思呢?假设光盘存储的内容为:10101100110001,那么实际光盘会有三份这样的内容,假设我们在光盘某个位置刮花了,即二进制数据可能被修改了,那么当进行播放前,会将三份内容按照下面规则进行排列检验:

但是这样就会比较浪费存储空间,因为要存储一份内容,却要多花两倍空间,那怎么解决呢?

这就是本文将要引入的汉明码问题解析;

它所需要的检验错误的空间,只占整个内容的非常小一部分,它怎么实现的呢?我们慢慢道来

启发

在汉明发明汉明码之前,他知道存在一种奇偶检验算法,原理很简单,以16个数字块举例,第一个位置的值取决于后面15个位置中所有1的数量的奇偶,如果为奇数,那么第一个位置存储1,相反,存储0;(即保证16个块的所有1加起来为偶数,称为偶校验,相反的如果想加起来为奇数,则称为奇校验,我们这里只看偶检验)

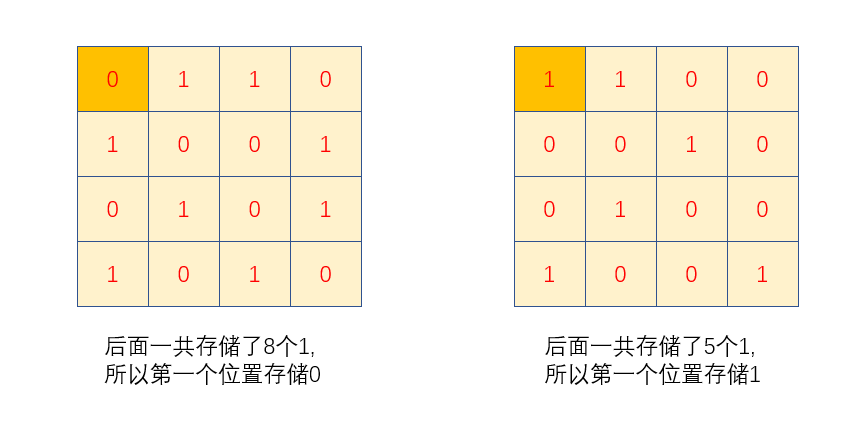
如果我们发送这样一种含有16个bit的01信息,我们便只需要检查1的数量是否为偶数,如果为偶数,则说明信息未变化,否则说明变化了;

比如第一个矩阵块的第三行,第三列的0变为了1,那么1的数量就会变成奇数,接收方就可以知道数据发生了改变;

有人会说:如果改变了两个位置呢?即可能多生出了两个1,或者减少了两个1,那不就没办法了吗?

是这样的,但是即使现在这么多高深的算法,也无法保证所有信息都能100%正确,我们只是在概率上相对保证了而已,今天我们介绍的这个算法也是这样,他只能校验奇数数量的改变的正确性;

此算法完美的将任何一个比特位发生的错误,都反映在了第一个比特位上,但是此算法存在一个问题—无法知道是哪个比特位发生了错误

汉明码介绍

于是汉明想出了以个方法,他将16个块进行了分组,然后在分组上进行偶校验,对于为啥在特定位置设置为校验位,最后会讲,大家可以把疑惑放一下:

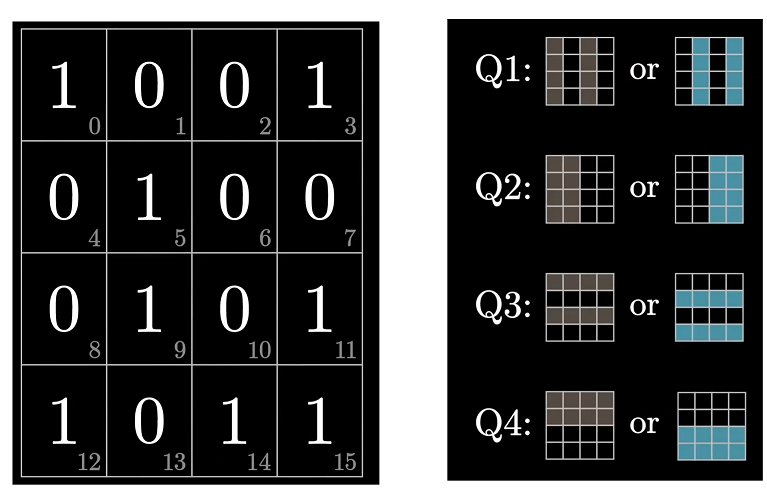
什么意思呢?

我们第一次先对位置全是奇数列的块进行分组,然后对1位置利用偶检验算法(即该位置的值取决于其他绿色区的所有1数量,如果相加为奇数,就需要该位置为1,保证所有绿色位置的1数量为偶数,相反,该位置填0)

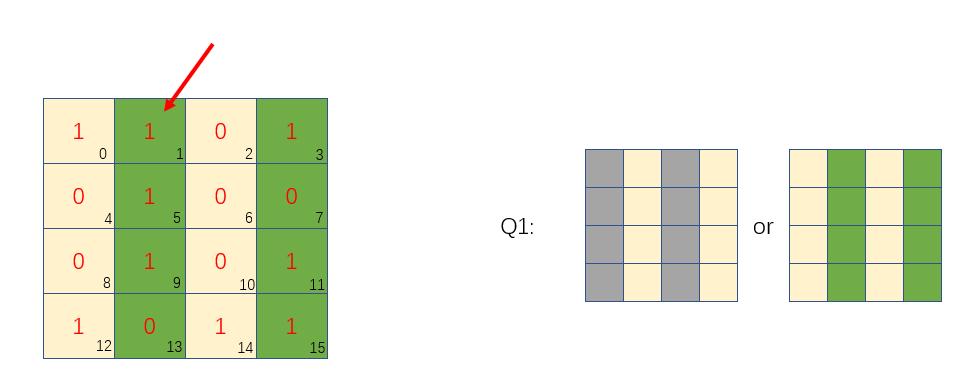
假设左边图绿色区域位置有一个位置的值修改了,即0变1,或者1变0,那么经过检验就会知道绿色区的1数量为奇数,所以可以判定错误发生在右边图绿色(其实就是左边图绿色)区域位置,相反,如果1数量为偶数,则可以说明发生错误位置在右边灰色区域位置(或者没有发生错误,但是先不考虑这个,后面会有介绍)

---

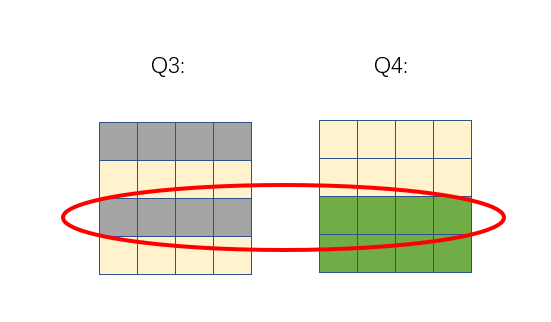
第二次是对右边一半的列进行分组,然后对2位置进行偶检验算法:

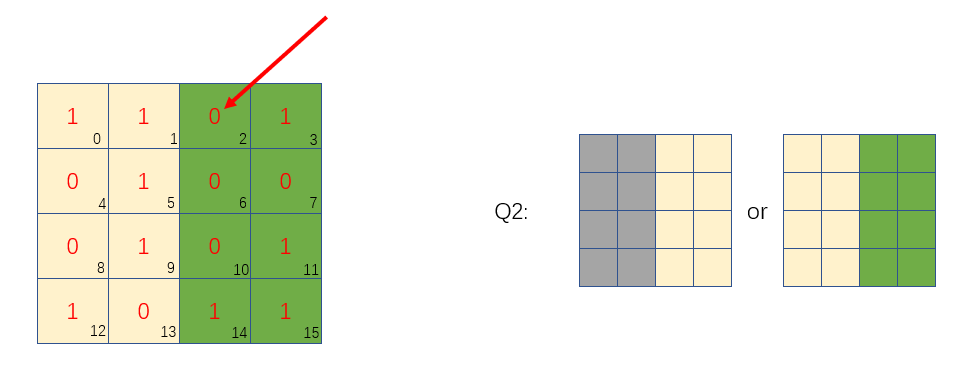
假设左边绿色区域位置有一个位置的值修改了,即0变1,或者1变0,那么经过检验就会知道绿色区的1数量为奇数,所以可以判定错误发生在右边图绿色区域位置,相反,如果1数量为偶数,则可以说明发生错误位置在右边灰色区域位置(或者没有发生错误,但是先不考虑这个,后面会有介绍)

好了,说到这里,我们仔细观察上面右边四个小图,是不是能发现,任意一个位置,发生错误,我们都可以通过求交集,确定错误发生的位置

精确在哪一列

比如,第9个位置的比特位发生了变化,1变成了0:

• 那么第一个分组可以检验到绿色区1的数量为奇数,从而确定发生错误的位置在第一个分组图的绿色区域位置;

• 那么第二个分组可以检验到绿色区1的数量为偶数,从而确定发生错误的位置在第二个分组图的灰色区域位置;

• 通过这两个图的交集,能够确定,发生错误的位置一定在第二列

  

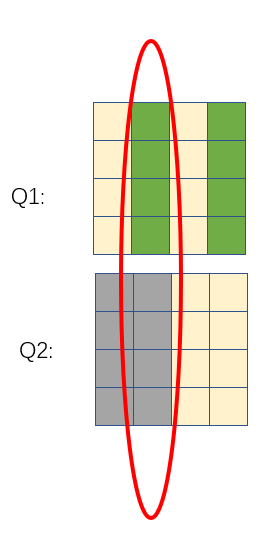
通过前面两个分组,你是不是有了启发,通过相同的方式进而确定发生错误的位置的行呢?是的,完全可以;

第三次分组,我们对第二行和第四行进行划分为一个小组,然后对4位置进行偶检验:

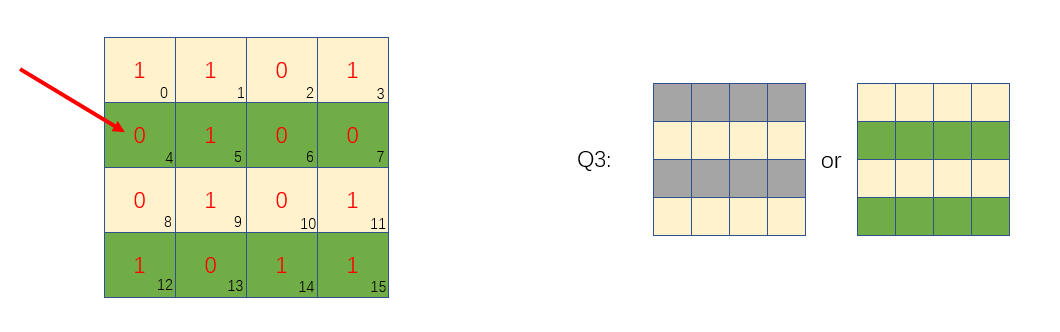
假设左边绿色区域位置有一个位置的值修改了,即0变1,或者1变0,那么经过检验就会知道绿色区的1数量为奇数,所以可以判定错误发生在右边图绿色区域位置,相反,如果1数量为偶数,则可以说明发生错误位置在右边灰色区域位置(或者没有发生错误,但是先不考虑这个,后面会有介绍)

第四次分组,我们对下半部分进行分组,然后对8位置进行偶检验:

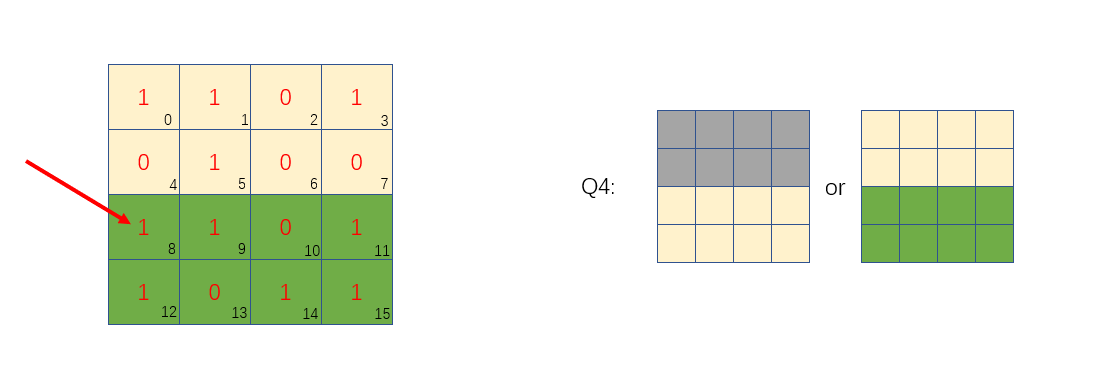
假设左边绿色区域位置有一个位置的值修改了,即0变1,或者1变0,那么经过检验就会知道绿色区的1数量为奇数,所以可以判定错误发生在右边图绿色区域位置,相反,如果1数量为偶数,则可以说明发生错误位置在右边灰色区域位置(或者没有发生错误,但是先不考虑这个,后面会有介绍)

到这里,我们还是假设9位置发生了错误,1变成了0:

• 那么第三个分组可以检验到绿色区1的数量为偶数,从而确定发生错误的位置在第三个分组图的灰色区域位置;
• 那么第四个分组可以检验到绿色区1的数量为奇数,从而确定发生错误的位置在第事个分组图的绿色区域位置;
• 通过这两个图的交集,能够确定,发生错误的位置一定在三行

通过一二分组,确定了错误发生在第二列,通过三四分组,确定了错误发生在第三行,也就是知道了错误发生在**[第二列,第三行]**位置,这样就完美且精确的确定了错误发生位置;

然后我们就可以将该位置的值改回去,这种算法比起之前的光盘算法来说,既节约了空间,又能精准定位位置,明显更优良

这里有个小问题:如果四个检验位(1,2,4,8位置),都没有检验出问题,即四次分组的绿色区域位置都是正常的,那只有两种可能

• 发生错误的位置都是四次分组的灰色区域,即第0位置(可以根据我上面四种分组方法去求交集得到该结果,这里不再赘述)
• 没有发生错误

也就是说,通过四个检验位,我们可以精确的确定发生错误的位置有16种可能性,且能精确定位出第[0-15]位置,但是没有发生错误这第17种可能性,我们却没办法解决,那怎么办呢?

答案是: 直接忽略第0位置,这样子当我们四个检验位都检查出来是偶数时候,说明数据正常,没有错误发生

当然,真正的大佬怎么可能会就这样浪费掉一个位置呢?他们把第0位置设置成了全局校验位,即它的值取决于除了它之外的所有位置的1的数量奇偶性,如果其他位置1数量之和为奇数,那么第0位置填1,相反填0,总之就是保证全局16个位置的1数量为偶数,我们称为全局偶校验;

这有什么作用呢?那就是我们可以监测出至少两个位置发送错误,比我们之前所说的局限性只能检验奇数变化多了一种可能性

比如第5号位置,和第9号位置都发生了错误:

• 那么全局校验位为0
• 同时通过另外四个校验位,我们可以找出第9号位置发生了错误

也就是说,当全局校验位为偶数,但是另外四个校验位检测出错误时候,表明至少有两个错误;因为如果只发生了一个变化,全局校验位应该为奇数

(注意哦,博主这里说的校验位为奇偶,不是指校验位(1,2,4,8)位置的值为1或者0,而是指它们所属的分组(绿色或者灰色)的所有位置加起来的1数量)

在我们日常生活中,无论要发生多少信息,都是把所有信息分为11个bit位为一组(因为第0位置,和另外四个校验位一共占据了5个位置),进行填充16块的矩阵,比如这里有信息: 00110001110,该怎么将它填入方框呢?答案如下:

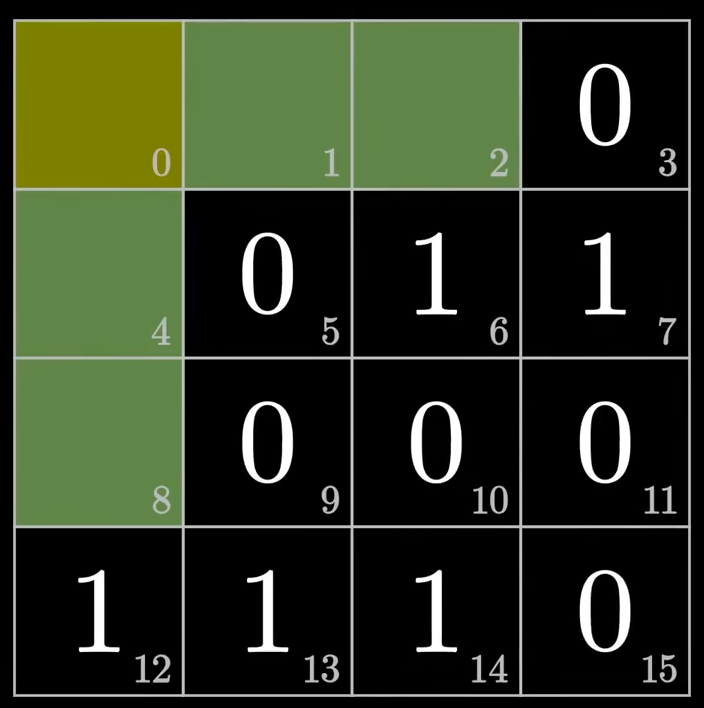
现在,我们可以根据之前讲的四种分组分别对四个校验位进行填充,最后对全局校验位进行填充:

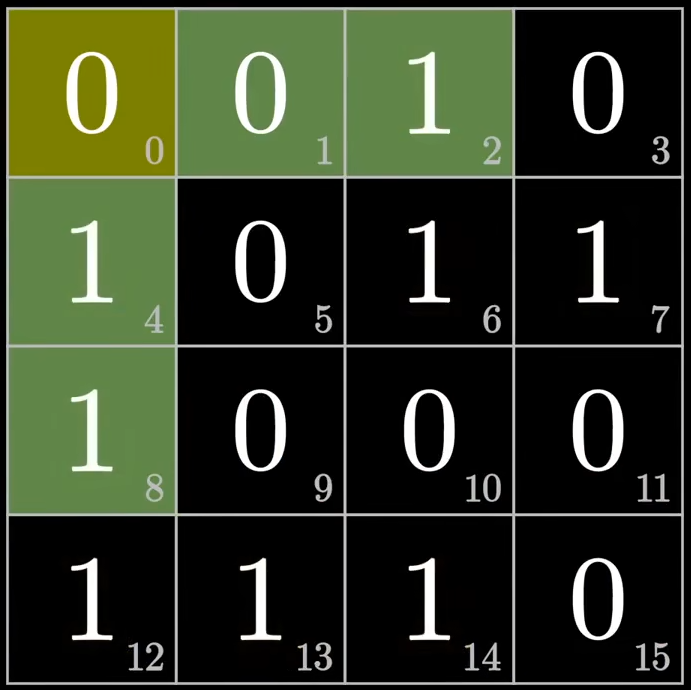
现在,假设你是发送方,你给对面发送了一个上面信息的数据块,但是数据传送过程中发生了错误,对面根据汉明码的检验,怎么进行确定发生错误并修改呢:

• 第一个校验位为偶数(要记得之前博主提醒的不是说第1位置为0,而是之前说分组位置的所有1数量),说明发生错误的位置在第一列和第三列

• 第二个校验位为奇数(因为有5个1),说明发生错误的位置在第三列和第四列

  通过第一和第二校验位,我们可以判定发生错误的位置在第三列

• 第三个校验位为偶数 ,说明发生错误的位置在第一行和第三行

• 第四个校验位为奇数,说明发生错误的位置在第三行和第四行

  通过第三和第四校验位,我们可以判定发生错误的位置在第三行

• 通过四个校验位,我们知道了发生错误的位置在第三行第三列,即第10号位置

• 全局校验位为奇数,那说明只有一个地方发生了错误,(毕竟三个,五个这种多奇数错误,我们也不知道,这种算法的默认前提就是只发生一个错误)

因此对面就可以更改第10位置,然后正确使用信息;

怎么实现汉明码?

为了实现汉明码,你可能会写一个算法,对可能发生错误的每一个位置进行检测,比如检测每个分组,然后记录结果,最后求交集,对吗?

是不是感觉非常繁琐呢?

但实际上,这却比你想象中的简单的多,我们以图中7号位置发生错误为例,那么第一分组,第二分组,第三分组的检验位都是奇数,而第四分组的检验位却为偶数.

我们把分组顺序按照第四,第三,第二,第一,这样排序,认为奇数检验结果为1,偶数检验结果0,那么可以得到这样结果0111,变成10进制就是7,而第7号为正好是发生错误的位置!!!

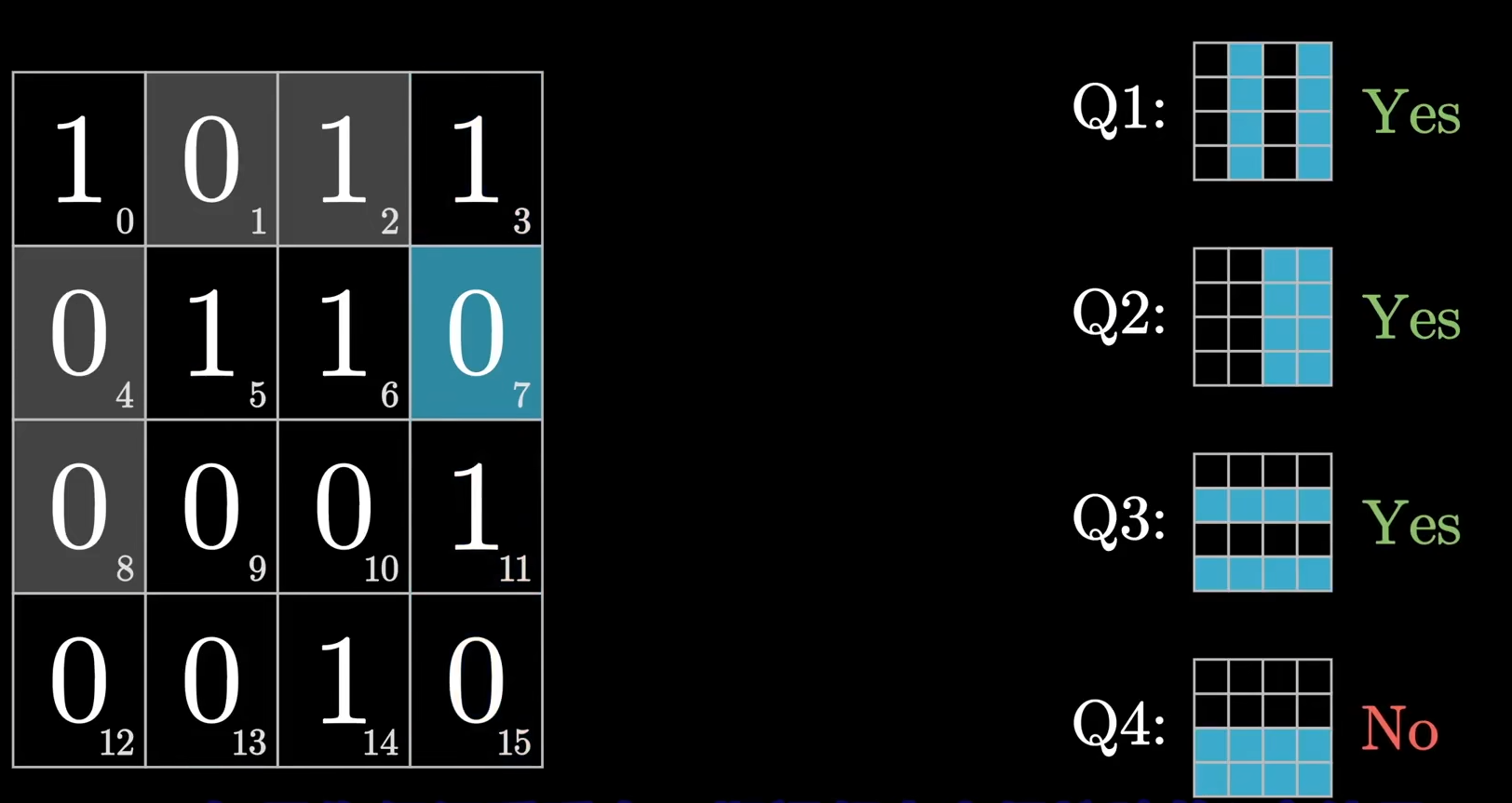
是不是感觉很神奇?因为:

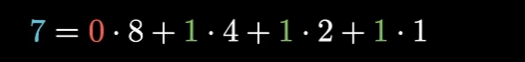
换种说法,第7号位置发生错误,只影响了第一分组,第二分组和第三分组,而他们的校验位位置就是1,2,4;但是没有影响第四分组,所以8并没算进来

还不明白?那我们把0-15这16个位置编号转换为二进制,然后我们先看所有二进制最后一位为1的列,这刚好就是我们的第一分组,如果在这个分组上面发生了错误,就相当于在说:

• 如果这里有错,是不是发生错误的位置,最后一个比特位为_ _ _ 1呢???(1代表检验位为奇数,发生了错误,上面说过)

我们在看倒数第二个比特位全是1的列,是否相当于在说:

• 嘿,又是我,如果这里有错,是不是发生错误的位置,倒数第二个比特位为_ _ 1 _呢?

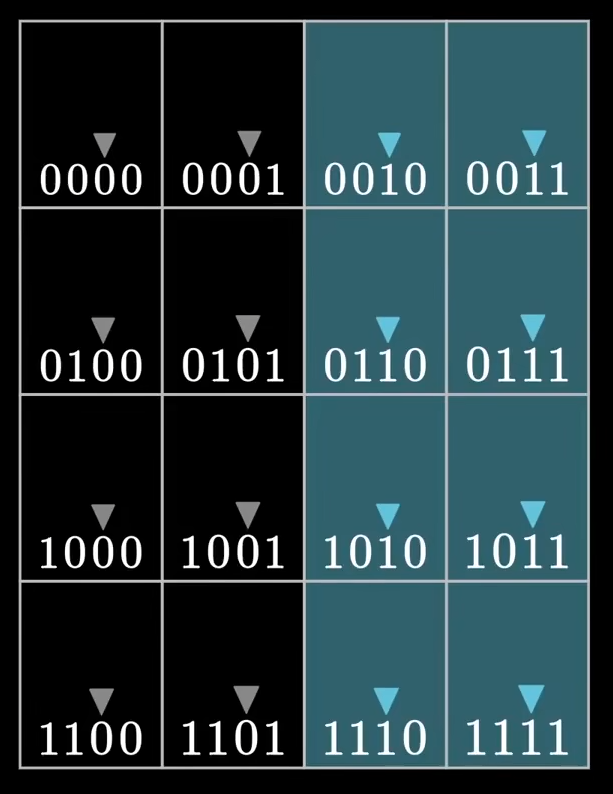
同样道理,我们在看倒数第三个比特位全是1的行,是否相当于在说:

• 嘿嘿,还是我,如果这里有错,是不是发生错误的位置,倒数第三个比特位为_ 1 _ _呢?

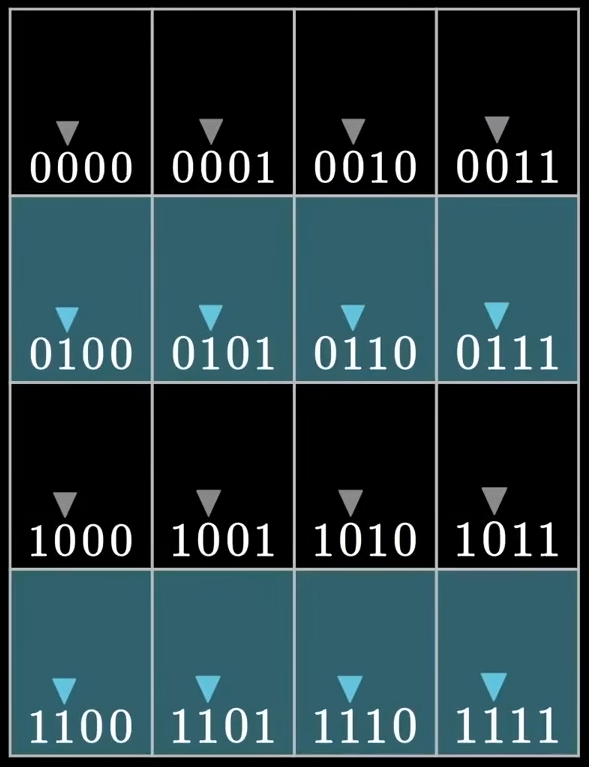
最后,我们在看第一个比特位全为1的行,是否相当于在说:

• 嘿嘿嘿,同样是我,如果这里有错,是不是发生错误的位置,倒数第三个比特位为0 _ _ _呢?(因为第四个分区校验位为偶数,代表没错,所以为0)

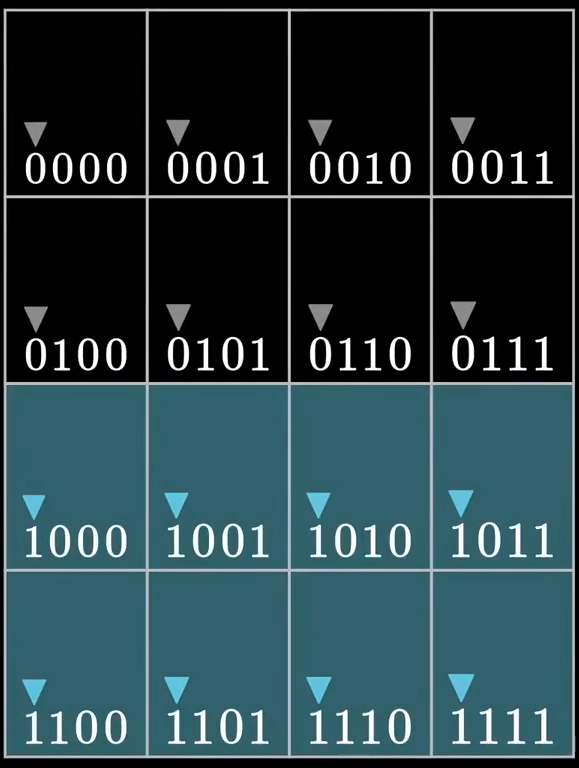
那我们把四次校验结果汇总,不就是像下面这样吗?

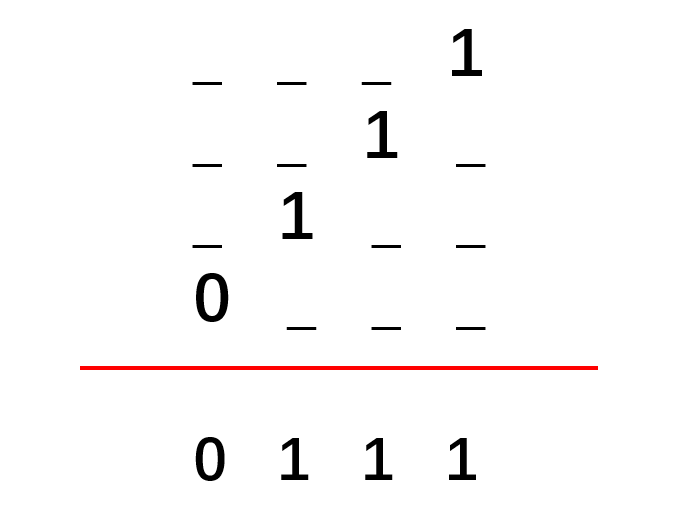
出现1比特位的物理位置刚好是第一分组,第二分组,和第三分组位置的交集,也就是第7位置,而第四分组并不包含第7位置,所以为0,

而0111转变为10进制后也就是7

怎么实现更高模块的汉明码?

通过上面的解释,想必我们也知道了为啥要这样进行分组

那么我们现在想要进行扩展,不适用16个块了呢?而是使用64个块呢?其实本质还是一样,我们照例把0-63位置变成二进制,然后根据对应比特位全是1和行或者列进行分组,比如第一个比特位全是1的行为一个分组:

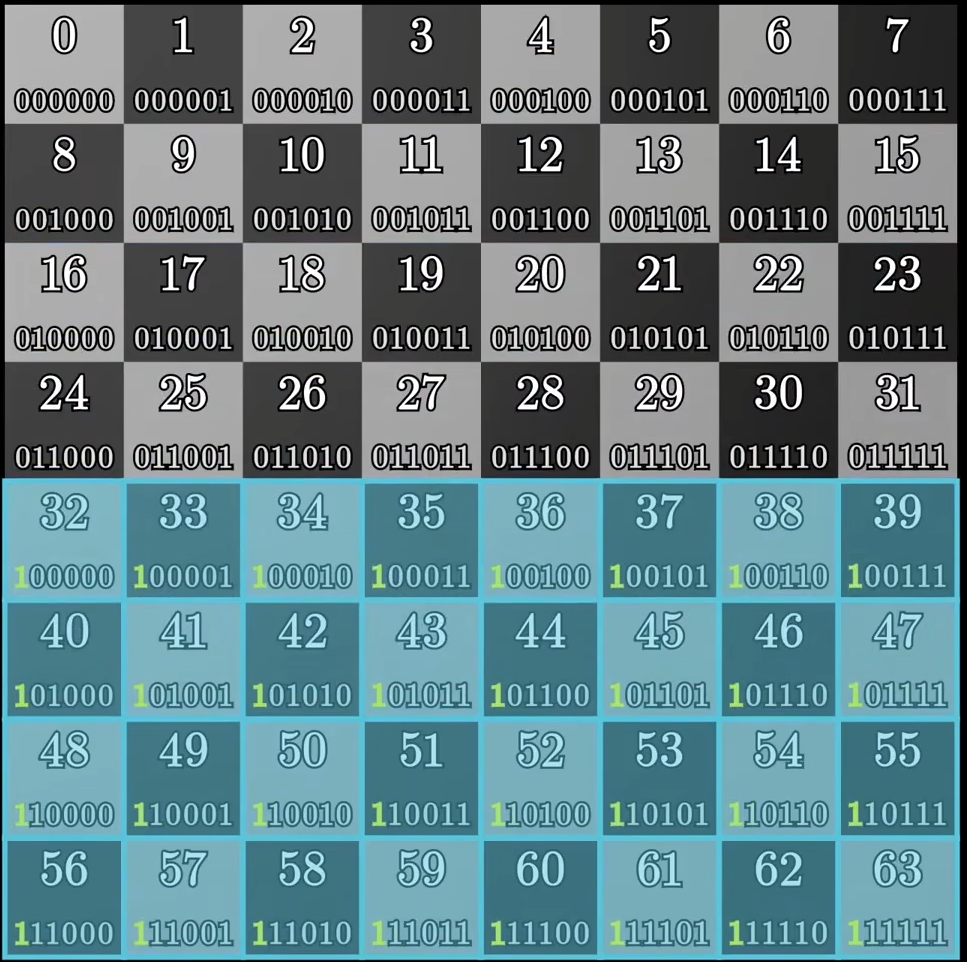
至于其他更多可能性分组划分的罗列,这里就不做赘述了;

为什么校验位一定是2的n次方?

1,2,4,8,16等都是2的幂次方,如果把他们换算成二进制,是因为它们只有一个比特位为1,这意味着1,2,4,8等这种奇偶校验位有且仅有可能分别落在第一分组,第二分组,第三分组,第四分组等位置,而不可能落在其他分组

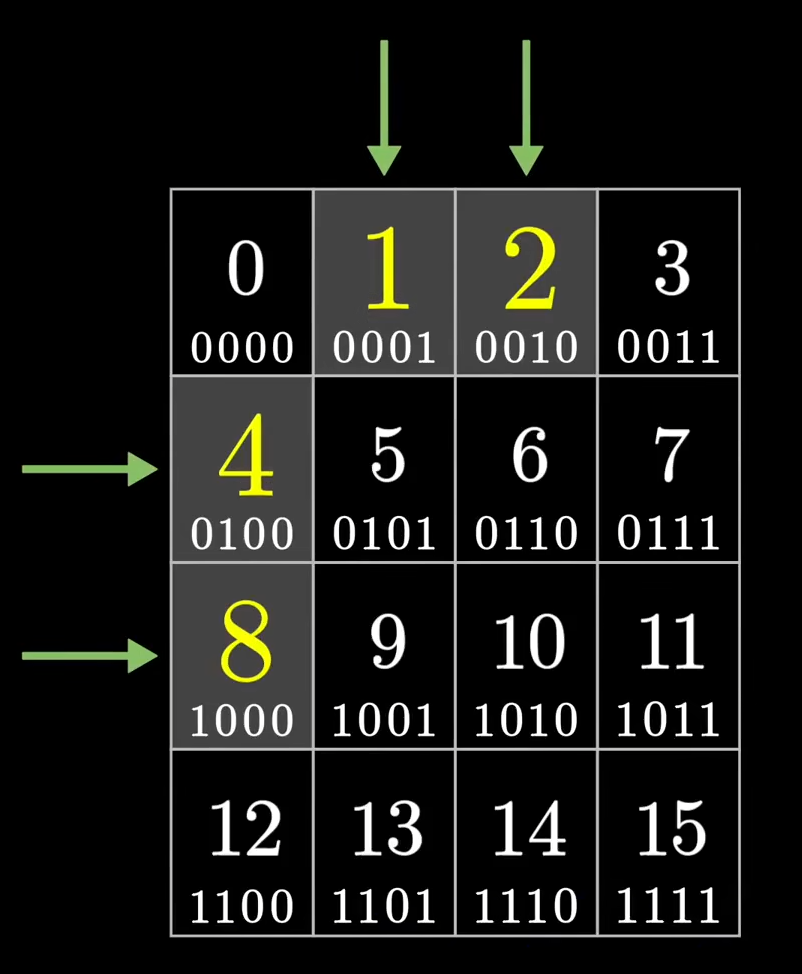
例如校验位4,它的二进制为0100,而它只可能属于倒数第三个比特位全1的行分组里面,而不会落在其他分组;

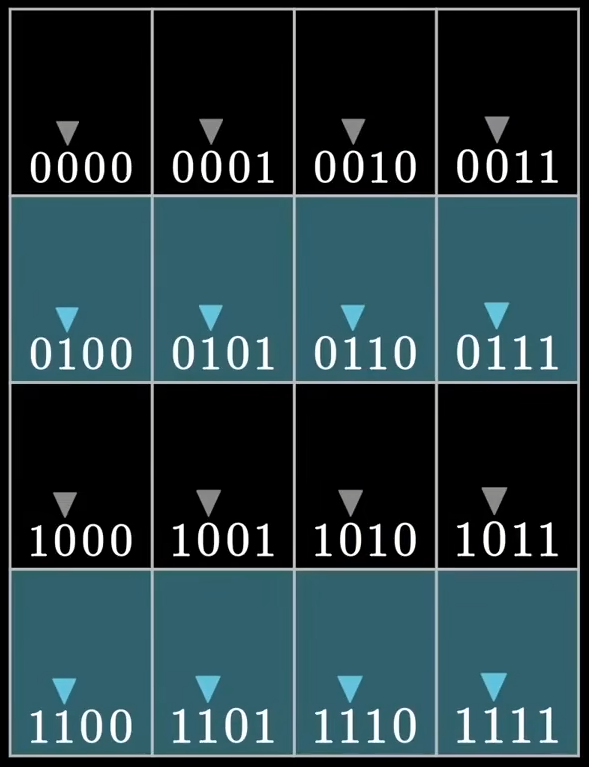
用更简洁的方式理解汉明码

如果说前面的方式都是在用巧妙的方式告诉我们错误位置的二进制表达,那我们可以用另一个角度进行看待: 异或

异或的特性是,相同为0,不同为1

• 0 ^ 0 = 0;
• 1 ^ 1 = 0;
• 1 ^ 0 = 1;
• 0 ^ 1 = 1;

换言之,异或结果就是对于待异或比特位的奇偶校验位

现在我们根据这个特性,去看看怎么进行对汉明码求解错误位置,以下面图中10号位置出错(可以通过之前的分组方法求出来)为例:

我们把所有存储值为1的位置的编号转变为二进制进行异或:

得到的结果就是1010,换算成10进制就是10;

为什么呢,请看下图:

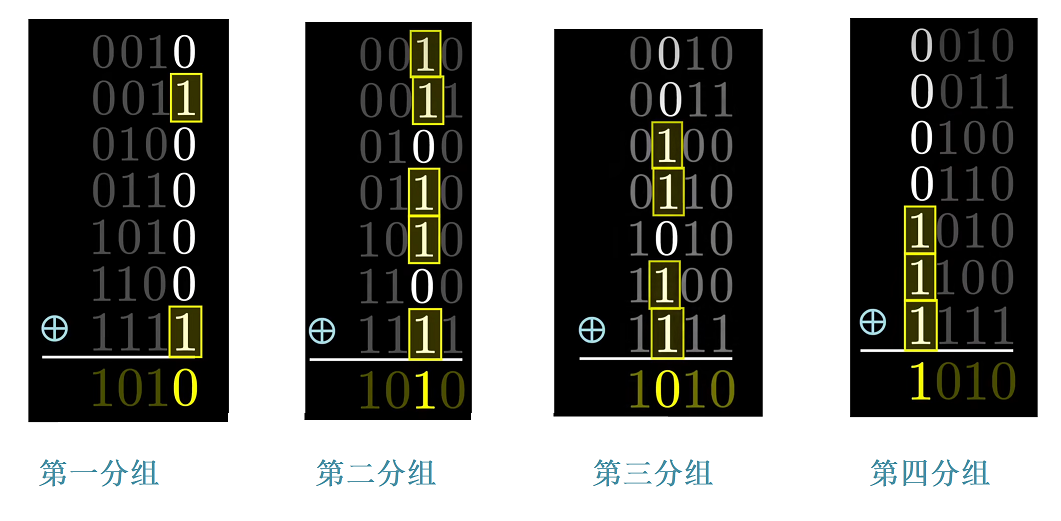
• 我们只看最后一个比特位为1的值,它们刚好是第一分组位置存储值1的位置编号(3和15)
• 再看倒数第二个比特位为1的值,它们刚好是第二分组位置存储1的位置编号(2,3,6,10和15)
• 再看倒数第三个比特位为1的值,它们刚好是第三分组位置存储1的位置编号(4,6,12,15)
• 同理,第一个比特位为1的值,它们刚好是第四分组位置存储1的位置编号(10,12,15)

而每一列的异或值,可以说是一个校验位,就类似于最上面介绍的那种方法,在问:

出错位置是不是在第一分组啊?_ _ _ 0,答: 不是

出错位置是不是在第二分组啊?_ _ 1 _, 答: 是

出错位置是不是在第三分组啊? _ 0 _ _,答: 不是

出错位置是不是在第四分组啊? 1 _ _ _,答: 是

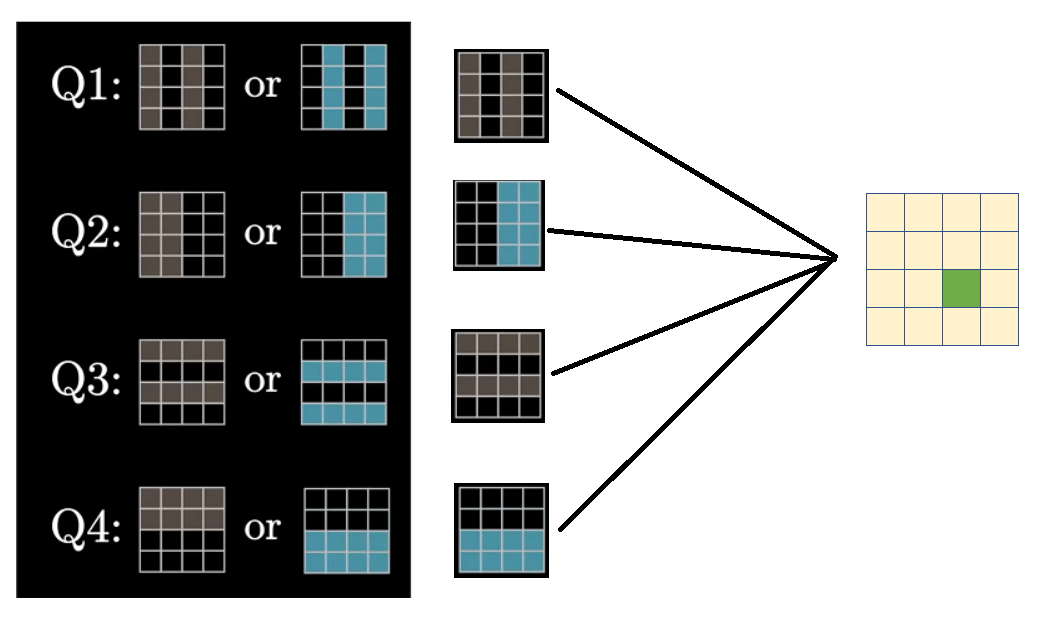
将他们组合起来就是1010,意思是,不在第一分组,在第二分组,不在第三分组,在第四分组,用图求交集的话,就是下面这样: