1 . 人脑是怎么认识到物体的

在谈卷积之前，我们先来了解一下人是怎么认识物体的。
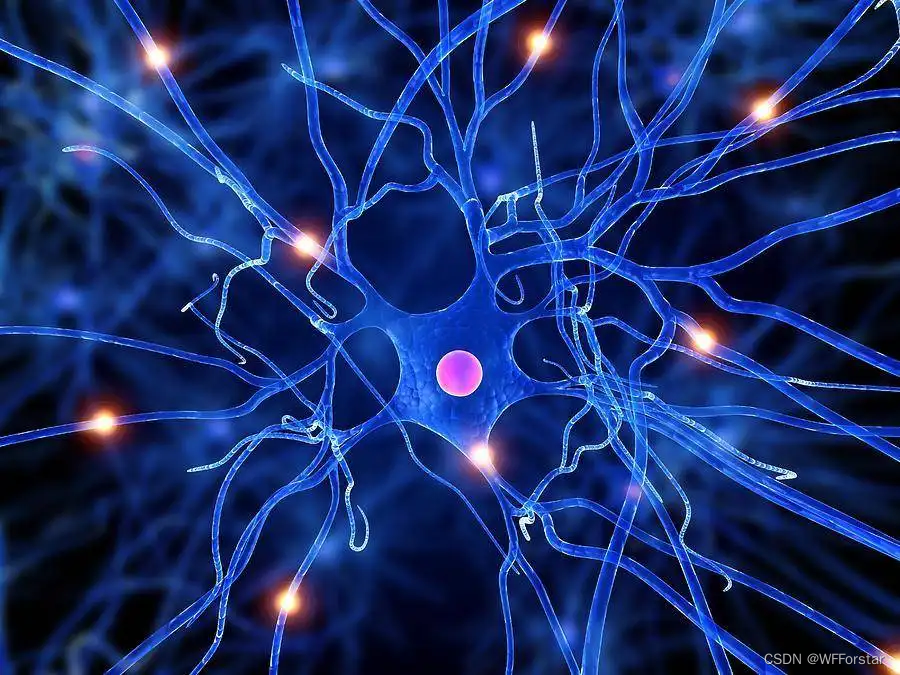
人脑是个非常复杂的结构，是由无数个神经元连接起来，每个神经元都有自己负责记忆的东西。当人眼看到物体的时候，视神经就会将看到的东西一步一步往后传直到脑神经。
当然，神经元不可能总是处于激活态。假设你眼睛看见了一只狗狗，那记住狗的神经元就会一层一层的传递下去信息”这是一只狗“，直到在最后输出”狗“的结论。
每个神经元都记忆着不同的东西，只有当遇到他认识的物体的时候，才会激活，否则就是静止。
那么换算到计算机中，很容易想到，激活就是乘1操作，静止就是乘0操作。
在深度学习的神经元中，当然不可能只是0或者1这么简单的数字了，而是一个叫做“权值”的东西，神经元可以通过权值的加权运算来判断是否让信息传递到下一层。比如神经元判断出95%是猫，那基本就是只猫，就会传递到下一层神经元中。
那权值是怎么计算的呢？就要请出卷积了。

2. 卷积

作为当代理工科大学生，不可避免的，肯定听说过卷积这个词，不管在数字信号处理还是啥啥其他科目中，一直没绕开卷积这个词，下面这个卷积公式想必也是非常熟悉。

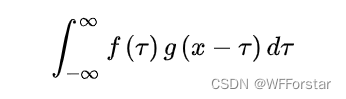
今天要谈谈的，不需要卷积这个前提知识，哈哈。因为深度学习中卷积的作用就是模拟人眼看物体的过程。如下图所示

这其中，不停移动的3*3的卷积核，就是人的视野范围，给一个专业名词叫做感受野。而卷积过程，就是用3x3的卷积核，去逐步扫描图片。横着扫完竖着扫。每扫一次，就将逐个像素点的值相乘然后加一起，得到一个输出。
在实际的操作中，我们可以修改不同的卷积核的大小，来改变感受野的大小，从而实现对物体不同特征的提取，这也是卷积算法的核心。

3. 卷积核

通过第一节的学习，我们知道了一个图片在计算机中可以这么表示：[n,h,w,c]。
但实际上，不论是图片，还是卷积核，其数学描述都是具有n,h,w,c四个维度的数据。
因此，对于卷积算法而言，输入图片尺寸为 [n, hi, wi, c]（下标i代表input，输入），卷积核尺寸为 [kn, kh, kw, c]，输出图片尺寸为[n, ho, wo, kn]（下标o代表output）。
结果发现，输出图片的channel数与输入图片的channel数不一致，反而与卷积核的个数一致。
这就有意思了，这意味着我们可以通过控制卷积核的数量来提取不同数量的特征，比如我有100个卷积核，那我就能提取100个不同的特征。
那么问题又来了，图像有什么特征呢？图像特征主要有图像的颜色特征、纹理特征、形状特征和空间关系特征。
颜色特征很容易理解，就是我们熟悉的RGB。
纹理特征就是图片的纹理，如下图

形状特征就是图片的形状，如下图

空间关系特征指图像中分割出来的多个目标之间的相互的空间位置或相对方向关系，这些关系也可分为连接/邻接关系、交叠/重叠关系和包含/包容关系等。通常空间位置信息可以分为两类：相对空间位置信息和绝对空间位置信息。前一种关系强调的是目标之间的相对情况，如上下左右关系等，后一种关系强调的是目标之间的距离大小以及方位。显而易见，由绝对空间位置可推出相对空间位置，但表达相对空间位置信息常比较简单。
事实上，计算机还能学到很多人类根本无法看出的特征，这些特征对深度学习来说也是非常重要的。
下面一篇文章我们将正式开始学习Resnet。