摘要

剑指Offer39 数组中出现次数超过一半的数字

本题常见的三种解法：

哈希表统计法：遍历数组 nums ，用 HashMap 统计各数字的数量，即可找出众数。此方法时间和空间复杂度均为 O(N) 。
数组排序法：将数组 nums 排序，数组中点的元素一定为众数。
摩尔投票法：核心理念为票数正负抵消。此方法时间和空间复杂度分别为 O(N) 和 O(1) ，为本题的最佳解法。

一、哈希表统计法

1.1 哈希表统计法思路

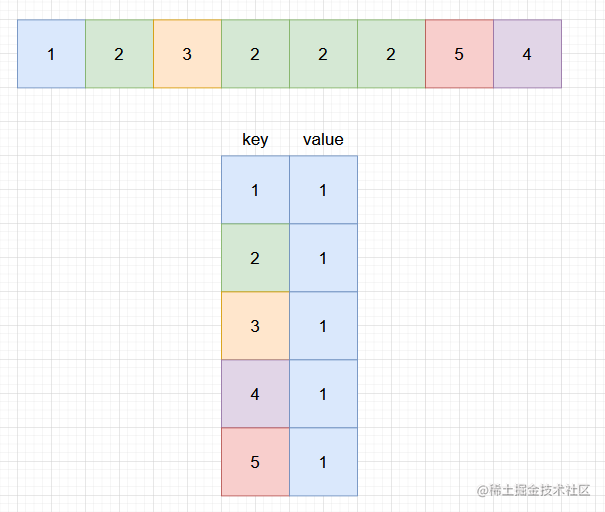
我们知道出现次数最多的元素大于 n/2 次，所以可以用哈希表来快速统计每个元素出现的次数。
我们使用哈希映射（HashMap）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。

我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后，我们遍历哈希映射中的所有键值对，返回值最大的键。我们同样也可以在遍历数组 nums 时候使用打擂台的方法，维护最大的值，这样省去了最后对哈希映射的遍历。

图片.png

1.2 复杂度分析

时间复杂度：O(n)，其中 nn 是数组 nums 的长度。我们遍历数组 nums 一次，对于 nums 中的每一个元素，将其插入哈希表都只需要常数时间。如果在遍历时没有维护最大值，在遍历结束后还需要对哈希表进行遍历，因为哈希表中占用的空间为 O(n)。
空间复杂度：O(n)。需要存储数组的相关元素到Hashmap中。

1.3 code 示例

/**
 * @description 利用Hashmap的方式的 时间O(n) 空间是O(n)
  * @param: nums
 * @date: 2022/12/7 9:30
 * @return: int
 * @author: xjl
*/
public int majorityElement(int[] nums) {
    HashMap<Integer, Integer> map=new HashMap<>();
    for (int i:nums){
        if (!map.containsKey(i)){
            map.put(i,1);
        }else {
            map.put(i,map.get(i)+1);
        }
    }
    for (int i:map.keySet()){
        if (map.get(i)>nums.length/2){
            return i;
        }
    }
    return -1;
}

二、数组排序法

2.1 数组排序的思路分析

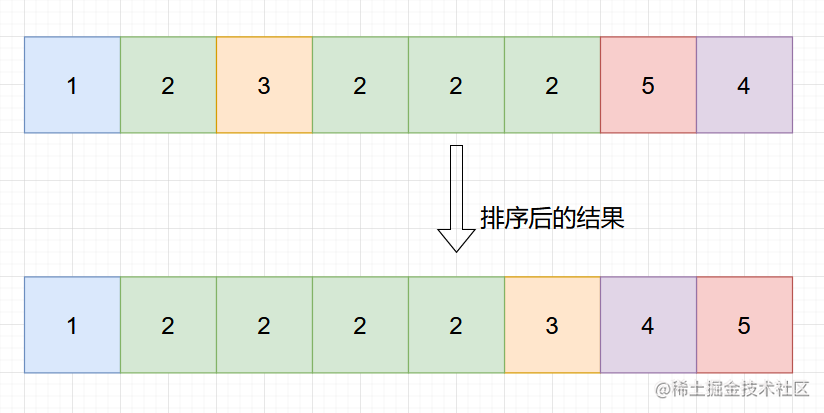
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为 n/2的元素（下标从 0 开始）一定是众数。

对于这种算法，我们先将 nums 数组排序，然后返回上文所说的下标对应的元素。下面的图中解释了为什么这种策略是有效的。在下图中，第一个例子是 n 为奇数的情况，第二个例子是 n 为偶数的情况。

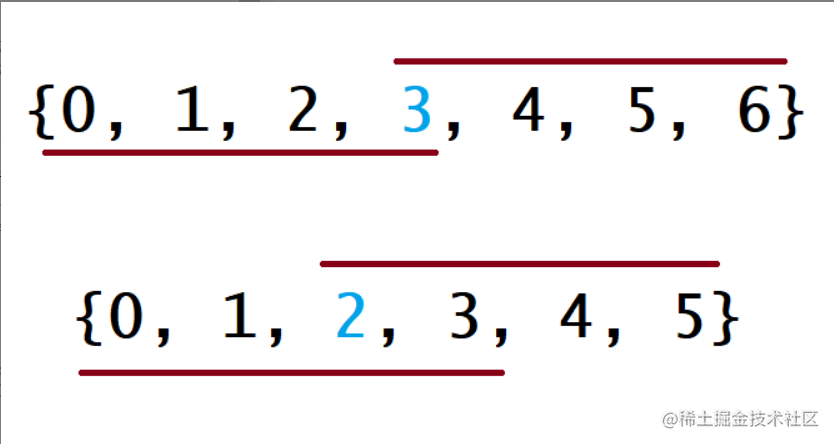
图片.png

对于每种情况，数组下面的线表示如果众数是数组中的最小值时覆盖的下标，数组下面的线表示如果众数是数组中的最大值时覆盖的下标。对于其他的情况，这条线会在这两种极端情况的中间。对于这两种极端情况，它们会在下标为 n/2的地方有重叠。因此，无论众数是多少，返回 n/2 下标对应的值都是正确的。

图片.png

2.2 数组的排序的复杂度分析

时间复杂度：O(nlog⁡n)。将数组排序的时间复杂度为 O(nlog⁡n)。
空间复杂度：O(log⁡n)。如果使用语言自带的排序算法，需要使用 O(log⁡n) 的栈空间。如果自己编写堆排序，则只需要使用 O(1) 的额外空间。

2.3 code 示例

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

三、摩尔投票法

3.1 数组排序的思路分析

核心理念为 票数正负抵消 。设输入数组 nums 的众数为 x ，数组长度为 n 。

推论一: 若记众数的票数为+1 ，非众数的票数为−1，则一定有所有数字的票数和>0。
推论二：若数组的前a个数字的票数和 =0 ，则数组剩余(n−a)个数字的票数和一定仍>0 ，即后 (n−a)个数字的众数仍为x。

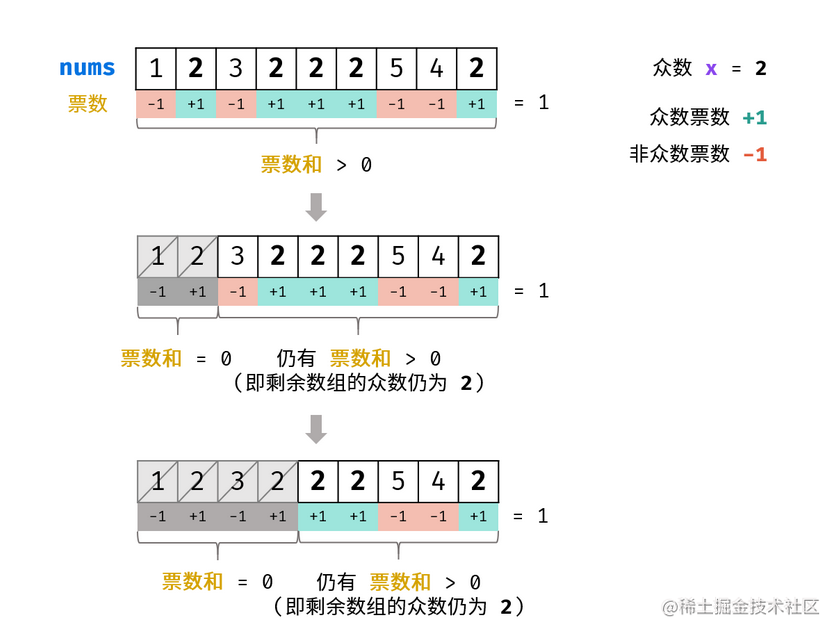
图片.png

根据以上推论，记数组首个元素为n1，众数为x，遍历并统计票数。当发生票数和=0时，剩余数组的众数一定不变，这是由于：

当 n1=x：抵消的所有数字中，有一半是众数 x 。
当 n1≠x：抵消的所有数字中，众数 x的数量最少为0个，最多为一半。

利用此特性，每轮假设发生票数和=0都可以缩小剩余数组区间。当遍历完成时，最后一轮假设的数字即为众数。

算法流程:

初始化：票数统计 votes = 0 ，众数 x；
循环：遍历数组 nums 中的每个数字 num ；
- 当票数 votes 等于 0 ，则假设当前数字 num 是众数；
- 当 num = x 时，票数 votes 自增 1 ；当 num != x 时，票数 votes 自减 1 ；

3.2 数组的排序的复杂度分析

时间复杂度 O(N) ：NN 为数组 nums 长度。
空间复杂度 O(1) ：votes 变量使用常数大小的额外空间。

3.3 code 示例

/**
 * @description 使用摩尔投票的方式来实现 当前为 vote=0 时候 就认为当前是众数 然后判断 后面是否是该数 如果是+1 如果不是-1 当等于0的时候更新的该数字 最后的就是众数就是该数了。
  * @param: nums
 * @date: 2022/12/7 10:06
 * @return: int
 * @author: xjl
*/
public int majorityElement3(int[] nums) {
    int count=1;
    int result=nums[0];
    for ( int i=1;i< nums.length;i++){
        if (count==0){
           result=nums[i];
        }
        if (nums[i]==result){
            count++;
        }else {
            count--;
        }

    }
    return result;
}