every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
瞬间感觉kmeans不香了,哈哈哈
说明: 该算法不仅能聚类,还能剔除离群点,聚类以后标签为-1的即噪声点(离群点),剔除即可。

1. 正文
1.1 概念
DBSCAN(Density-Based Spatial Clustering of Applications with Noise) 基于密度的空间聚类。根据密度将数据划分成簇,可以在有噪声的空间中发现任意形状的簇。
1.1.1 形象化理解
现在有一群人,要在他们中发展微商。一个人只有发展直系亲属,且人数大于5个,微商才算做成功。通过这个规则,很容易在人群中划分出不同的“微商群”,即实现了聚类。(是不是很简短,有木有~)
1.2.2 一般概念
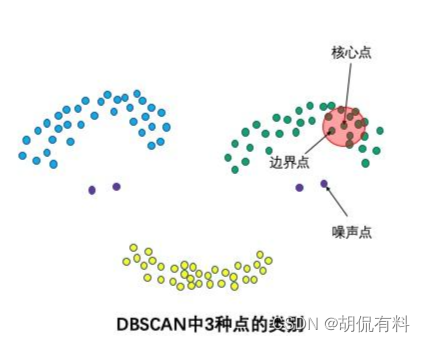
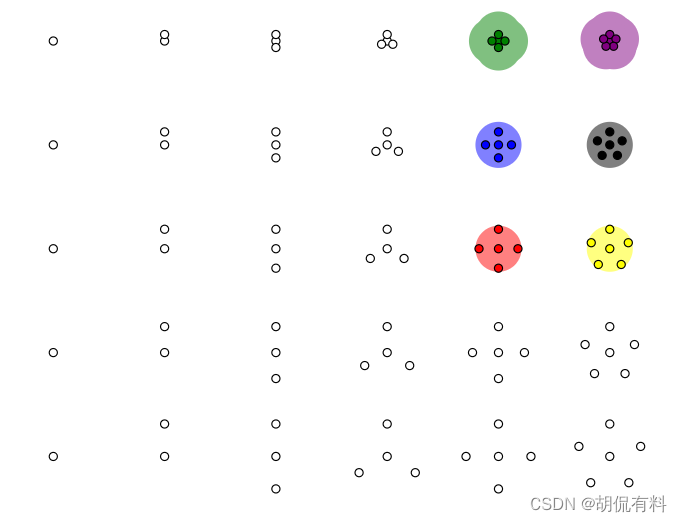
(1). 三种点
- 核心点
- 边界点
- 噪声点
如下图,一个点,如果在指定的半径内(上面所说的直系亲属,确定远近关系的)存在一定数量的其他点(上面的大于5,用于确定密度),则称该点为 核心点 ;
继续用半径和数量发展“下线”,直到最后无法满足规则未知,最后的“下线”称为边界点,不在簇中的点为噪声点。
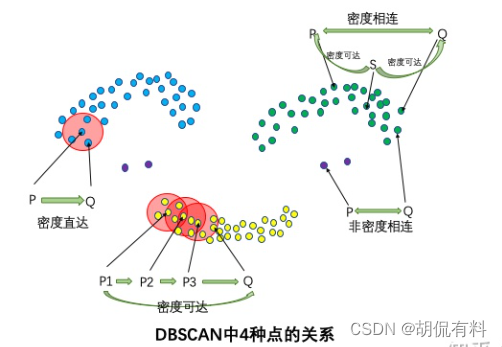
(2). 四种关系
- 如果P是核心点,Q在P的邻域内,则称P到Q密度直达
- 核心点到自身密度直达
- 密度直达不对称。(P到Q密度直达,Q到P不一定密度直达,注意: 上面微商的例子在这里不对,可以看数据点之间距离,应该比较好理解)
- 如果核心点P1到P2密度直达,P2到P3密度直达,…,Pn到Q密度直达 ,则,P1到Q密度可达 (密度可达同样无对称性,由密度直达不具有对称性,应该比较好理解)
- 如果存在核心带S,使S到P和Q都密度可达,则P和Q密度相连,密度相连具有对称性,密度相连的两个点在同一个聚类簇。
- 如果两个点不属于密度相连关系,则两个点非密度相连,非密度相连的两个点属于不同的聚类簇,或者其中存在噪声。
可以看下图理解:
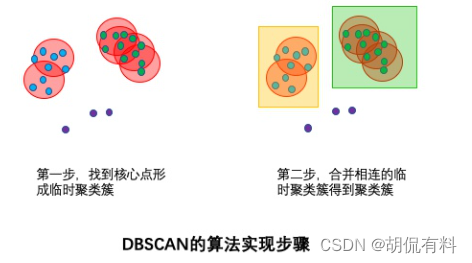
1.2 算法步骤
- 遍历所有样本点,如果指定半径内样本数大于指定的值,则当前样本纳入核心点列表,并将其密度直达的点形成临时聚类簇
- 对于每个临时聚类簇,检查其中的点是否为核心点,如果是,将当前点形成的聚类簇和当前点自身的临时聚类簇合并,得到新的临时聚类簇。(发展下线过程)
- 重复此过程,直到当前临时聚类簇中的每个点要么不在核心点列表中,要么其密度直达点都已经在该临时聚类簇。该临时聚类簇升级为聚类簇。
- 继续对剩余的临时聚类簇进行此过程。直到所有临时聚类簇被处理。
1.3 demo
说明:jupyter notebook里面运行
生成样本点
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import numpy as np
import pandas as pd
from sklearn import datasets
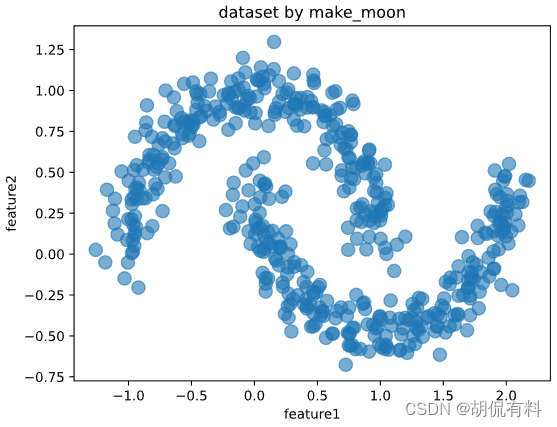
X,_ = datasets.make_moons(500,noise = 0.1,random_state=1)
df = pd.DataFrame(X,columns = ['feature1','feature2'])
df.plot.scatter('feature1','feature2', s = 100,alpha = 0.6, title = 'dataset by make_moon');
聚类
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
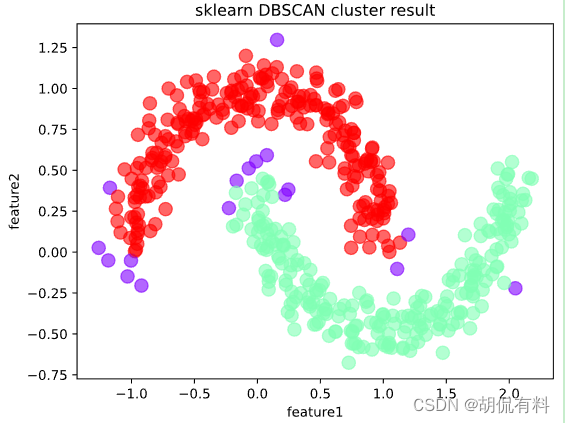
from sklearn.cluster import dbscan
# eps为邻域半径,min_samples为最少点数目
core_samples,cluster_ids = dbscan(X, eps = 0.2, min_samples=20)
# cluster_ids中-1表示对应的点为噪声点
df = pd.DataFrame(np.c_[X,cluster_ids],columns = ['feature1','feature2','cluster_id'])
df['cluster_id'] = df['cluster_id'].astype('i2')
df.plot.scatter('feature1','feature2', s = 100,
c = list(df['cluster_id']),cmap = 'rainbow',colorbar = False,
alpha = 0.6,title = 'sklearn DBSCAN cluster result');
1.4 eps值的设定
1.4.1 方法一:OPTICS算法
from sklearn.cluster import OPTICS
from sklearn.datasets import make_blobs
# 生成随机数据
X, y = make_blobs(n_samples=1000, centers=3, random_state=42)
# 使用 OPTICS 算法自适应估计 eps 值
optics = OPTICS(min_samples=10, xi=0.05)
optics.fit(X)
# 输出聚类结果和估计的 eps 值
print("Estimated eps:", optics.eps_)
print("Cluster labels:", optics.labels_)
1.4.3 方法二:K-距离
from sklearn.neighbors import NearestNeighbors
from sklearn.datasets import make_blobs
# 生成随机数据
X, y = make_blobs(n_samples=1000, centers=3, random_state=42)
# 计算 k-距离
knn = NearestNeighbors(n_neighbors=10)
knn.fit(X)
distances, indices = knn.kneighbors(X)
# 估计 eps 值
eps = distances[:, 9].mean()
# 输出估计的 eps 值
print("Estimated eps:", eps)
1.5 动画理解
推荐一个动画网站:
https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/
1.6 噪声点(离群点)显示
显示一维数据
def show_scatter_1D(data,labels,noise_black=False):
plt.clf()
if noise_black:
noise_data = data[labels == -1, 0]
plt.scatter(noise_data,np.zeros_like(noise_data), edgecolor='red',c='white', label='Noise')
for l in set(labels) - {-1}:
norm_data = data[labels == l, 0]
plt.scatter(norm_data, np.zeros_like(norm_data), cmap='viridis', label=f'Cluster {l}')
plt.legend()
plt.show()
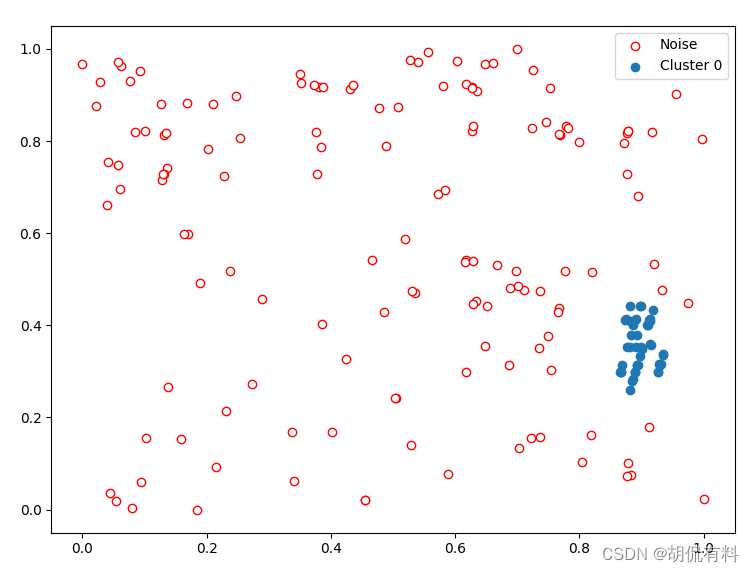
显示二维数据
def show_scatter_2D(data,labels,noise_black=False):
plt.clf()
if noise_black:
plt.scatter(data[labels == -1, 0], data[labels == -1, 1],edgecolor='red', c='white', label='Noise')
for l in set(labels) - {-1}:
plt.scatter(data[labels == l, 0], data[labels == l, 1], label=f'Cluster {l}')
plt.legend()
plt.show()
参考
[1] https://blog.csdn.net/swy_swy_swy/article/details/106130675
[2] https://blog.csdn.net/Cyrus_May/article/details/113504879
[3] https://blog.csdn.net/huacha__/article/details/81094891#t0
[4] https://zhuanlan.zhihu.com/p/336501183
[5] https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/