要开始了…内心还是有些复杂的
因为涉及到熵…单纯的熵，可以单纯
复杂的熵，如何能通俗理解呢…
我也没有底气，且写且思考吧

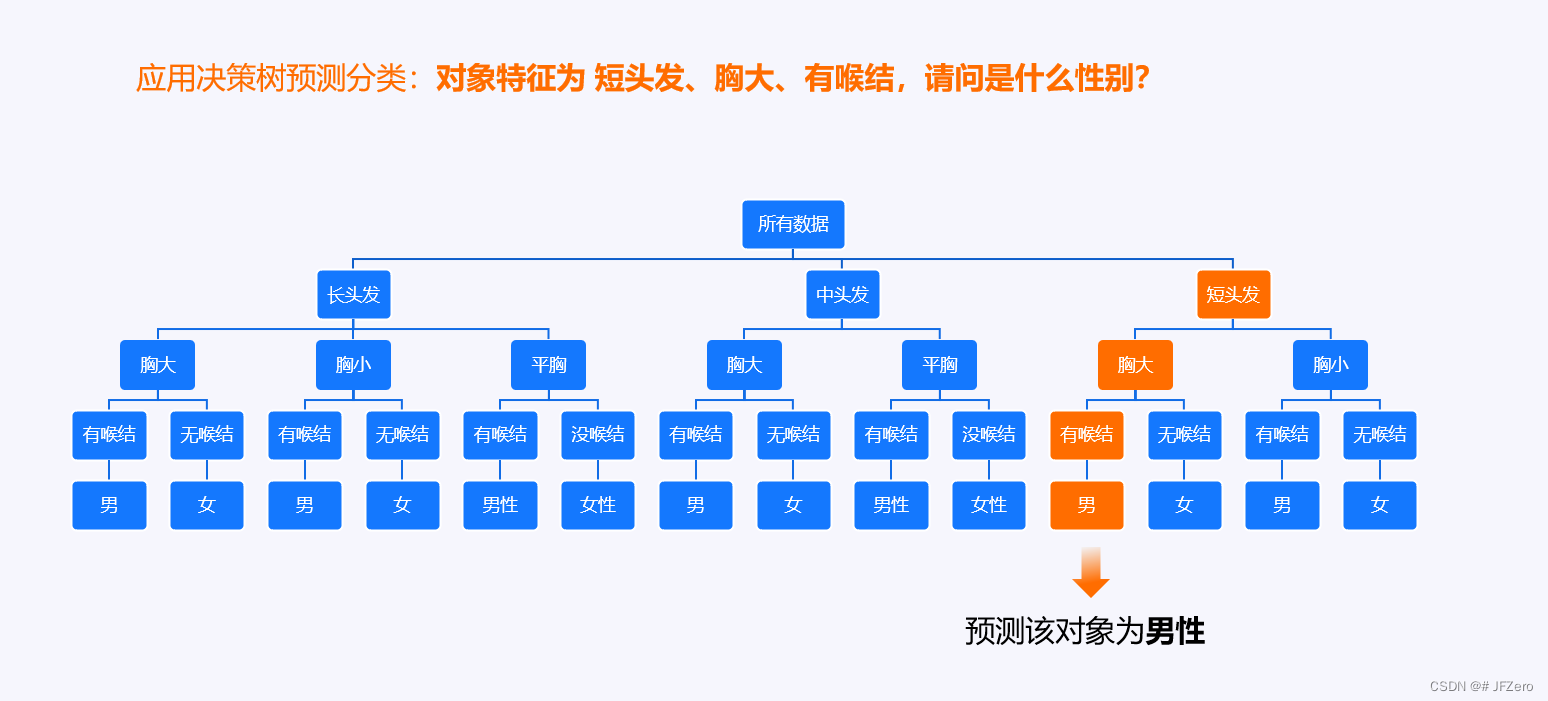
1. 决策树分类思想

首先，决策树的思想，有点儿像KNN里的KD树。

KNN里的KD树，是每次都根据某个特征，来将所有数据进行分类。

决策树也是，每次都根据某个特征，来将所有数据进行分类。

不同的是：

• KNN的KD树是一种二叉树，每次分类的特征，不一定能分干净，有可能下一次还会再根据这个特征进行分类。

• 决策树的分类是一种多叉树，每次分类的特征，都是应分尽分，分清楚分干净。
  

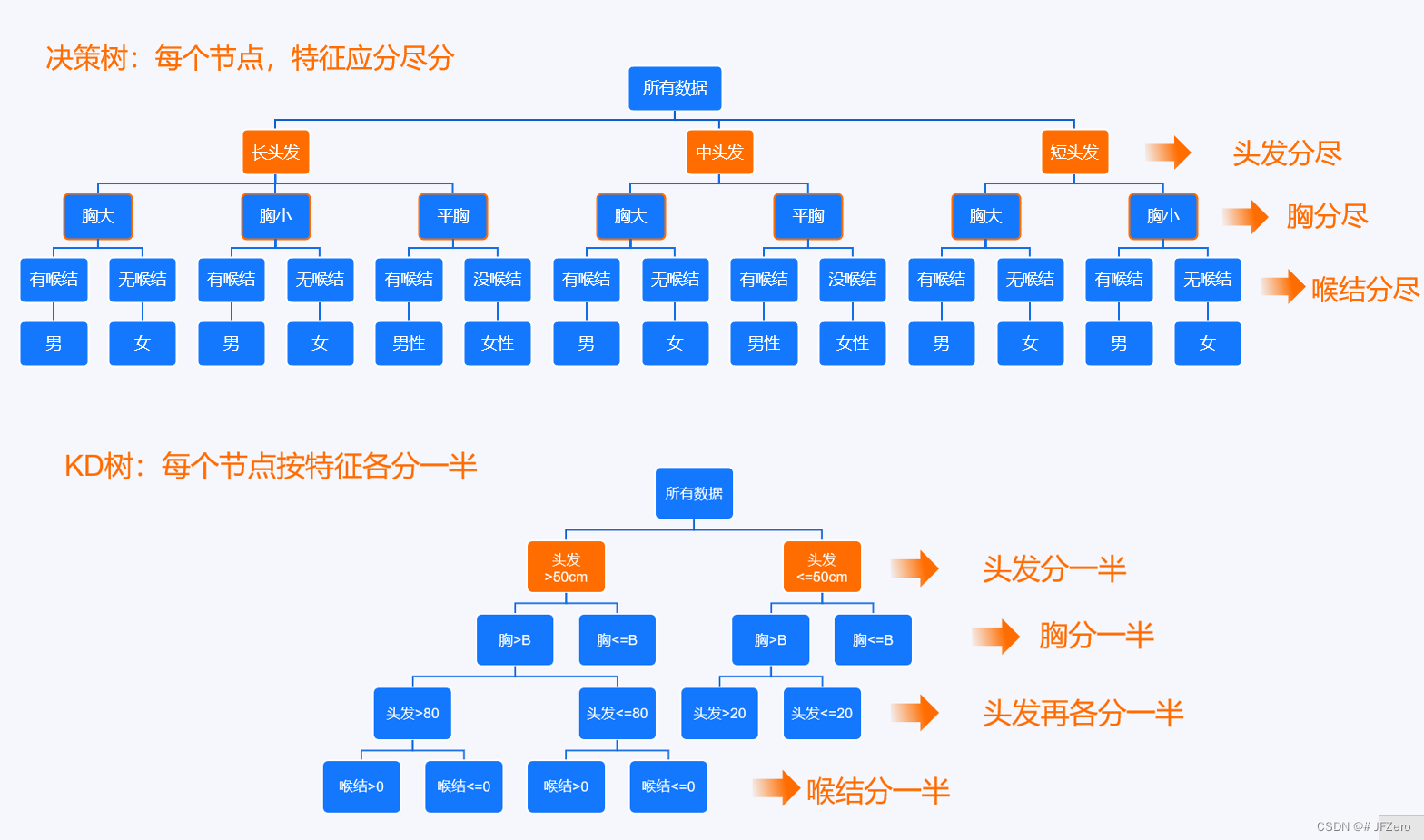
决策树什么时候停止划分呢？

当属性全被分完，或是类别唯一确定后，停止划分（还可以是其他条件）

当决策树划分好之后，我们如果要将某个对象进行分类，只需要从上往下，逐级按照各特征找到对应的类别即可。

按图索骥的思想

理想状态下，可以百分百分类正确

如果世界这么简单就好了，非黑即白的世界，谁不喜欢
我不喜欢…非黑即白的世界可太残酷了

实际上，常常是分不干净的

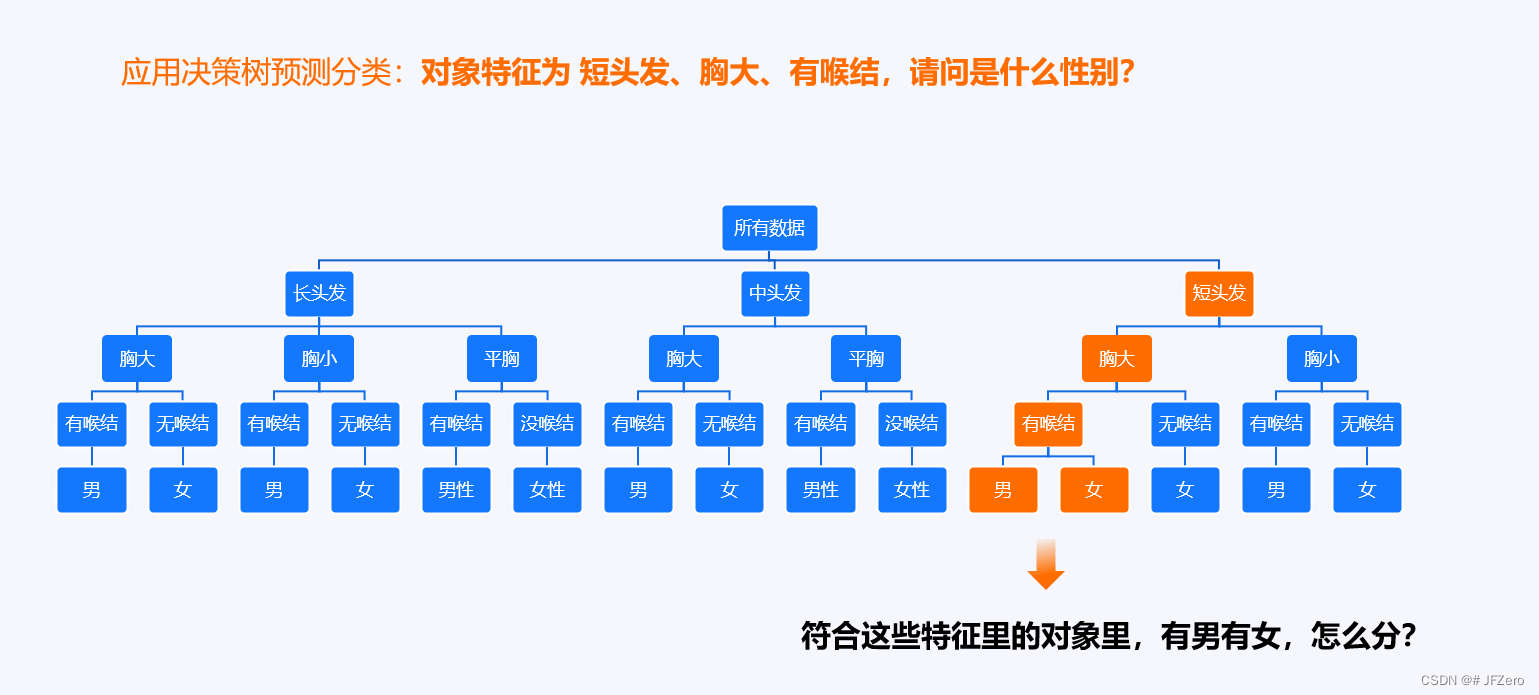
正常人的思维是，如果有男有女，就根据男、女占比来判断就好了嘛

• 如果这里头，男占比>女占比，就分类为男，反之分类为女

这是多么质朴的分类思想啊！

可惜有陷阱：特征的逐层筛选，有可能会因为某些无关特征，影响类别的占比

比如，头发长短对性别，实际是没什么关系的。

但由于我们提前筛选了头发这个特征，万一短头发里的人，只有俩人（一男一女）；或是短头发里的人，有喉结的男女比例刚好一样。

这种情况下，头发这个特征的分类，就会干扰到类别的预测！！！

我下意识就想到了朴素贝叶斯。
朴素贝叶斯分类也是这种问题，朴素贝叶斯是以条件独立为前提，通过概率来计算的，尽量避免了无关特征的干扰
其实，也可以用朴素贝叶斯，但现在要理解的是决策树！！！

为了减少这类可能无关或是相关性较低的特征对分类结果的影响，决策树的思想，是根据分类的纯度，来选择特征划分数据。

也就是，只要特征分的好，分类结果会更加纯粹，分类的确定性会更高。

什么是更纯粹的分类结果、确定性更高呢？

这就需要引入熵、信息增益、信息增益率等相关的信息学概念。

这是很困惑我的地方，尤其熵的解释
众说纷纭，但我看了很多，依然困惑
困惑在于，大家似乎都是给出了比较直观的解释，也就是用生活的比喻，告诉你熵就是这东西
就好像指着红苹果告诉我，红色就是红苹果这样的，红色就是红旗这样的，所以红就是这种颜色的…
但我依然不理解，为什么是这样的？

1.1 信息量

首先，讲到熵之前，必然要了解信息量。

信息量这个东西，也困扰了我很久，为什么它跟概率的关系是这样的：

信息量 $N=lo{g}_2(\frac{1}{P})$

说信息是以二进制为载体存储，ok，能理解为什么用2为底的log函数
但为什么是 $\frac{1}{P}$ 呢
然后我问，概率的倒数有什么意义？
伯努利实验告诉我，概率的倒数，表示该可能性发生需要进行的试验次数。
就比如抽中十万大奖的概率是$\frac{1}{100}$，那么需要进行 100次的抽奖才可能抽中
但…跟信息量有什么关系…
还有更多的解释是，定义就是这样的，B站也有举现实例子解说的
但我还是…缺少了点什么的感觉，理解不是特别深刻和通透

直到看到某个知乎博主的解释，我才恍然大悟。
信息量、熵更本源的解释

信息量，用于承载可能性结果的二进制存储位数。

例如要存储 4 种可能结果，一般是应用独热编码的方式表示：
00：第一种可能
01：第二种可能
10：第三种可能
11：第四种可能

因此，只需要 2 个位的二进制数，就能表示 4 种可能结果。

其实二进制的n个位（bit），可以表示 $2^n$种可能结果，这个是很基础的知识了

这 4 种可能结果的概率假设是相同的，那么每种可能结果的概率为 $\frac{1}{4}$

根据概率的倒数，表示为某实验（事件）第一次发生所需要进行的试验次数。

所需试验次数 $n=\frac{1}{P}$

那么，要使第一种可能结果发生，需要进行 $n=\frac{1}{P}次实验，即4$次事件（理想状态）

例如，婴儿屁屁有胎记的概率是1/4，
那么在 4 个婴儿里，我们要明确屁屁有胎记，理想状态下需要查看4个人的屁屁
第一个屁屁：无胎记
第二个屁屁：无胎记
第三个屁屁：无胎记
第四个屁屁：有胎记（其实不一定，但理想状态下是有的，天道好轮回嘛）

同样的，要使第二种可能结果发生，需要进行 $n=\frac{1}{P}次实验，即4$次事件（理想状态）

第三种、第四种结果也是如此。

因此，要得到一个明确的结果（无论是哪种结果），平均需要进行多少次实验呢？【重点在于平均】

那就是对每种可能结果的试验次数，进行加权平均求和，也就是
${\sum }_i{P}_i\ast n_i={\sum }_i{P}_i\ast \frac{1}{P_i}$

即 $\frac{1}{4}\ast 4+\frac{1}{4}\ast 4+\frac{1}{4}\ast 4+\frac{1}{4}\ast 4=4$

所以，要得到一个明确的结果，平均需要进行 n= 4 次实验（无论是哪种结果）

但这 n= 4 次实验，并不是我们说的信息量。

4 次实验的结果，存储在二进制位里，则需要$lo{g}_{2}n=lo{g}_{2}4=2$，需要 2 位的二进制存储位，这才是我们所需的信息量。

因此，n次实验，每次实验结果都存入一个二进制位，则需要$lo{g}_{2}n$个二进制位
即：$N=lo{g}_{2}n$

存储了实验结果的二进制存储数据量，正是我们所求的信息量N。

很合理吧，有结果，才有信息
没有结果的实验，只是一个没有信息的事件

因此，第一种可能结果的信息量为 $N=lo{g}_2(n)=lo{g}_2(\frac{1}{P})=lo{g}_{2}4=2$

第二种、第三种、第四种可能结果的信息量，也是这样计算出的，分别都是2

1.2 信息熵

那么，要明确结果（无论是哪种结果），平均需要多少信息量呢？

这就需要进行加权平均了嘛
${\sum }_i{P}_i\ast N_i=\frac{1}{4}lo{g}_{2}4+\frac{1}{4}lo{g}_{2}4+\frac{1}{4}lo{g}_{2}4+\frac{1}{4}lo{g}_{2}4=2$

因此，要明确结果，所需的平均信息量，实际就是我们所说的熵 H ！
$H={\sum }_i{P}_i\ast N_i={\sum }_i{P}_i\ast lo{g}_2(\frac{1}{P_i})$，

我忽然就悟了
也不知道是不是悟错了。。。

至于，为什么大家都说，熵越大的系统，不确定性越高呢？

首先，我们现在知道，熵是明确结果所需要的平均信息量。

熵越大，意味着，所需要的平均信息量就越大。

根据信息量与概率的关系 $N=lo{g}_2(\frac{1}{P})$，当熵越大，意味着平均的N越大，
2为底的log对数函数是递增函数，因此$\frac{1}{P}$也越大，那么 P 就越小

所以：熵越大→平均信息量N越大→确定结果的平均概率P越小

确定结果的平均概率P，P越小，说明结果越不确定
【就相当于是，系统明确是某个结果时的平均概率P，这与小球的概率是不同的东西了】

打个比方，对比两个抽奖箱

• 抽奖箱1号：红橙黄绿青蓝紫金粉银10种颜色的球，每种颜色各10个球，则每种球概率为1/10
  熵$H_1={\Sigma }_{i=1}^{10}(\frac{1}{10}\ast lo{g}_{2}10)=lo{g}_{2}10\approx 3.32193$
• 抽奖箱2号：99个白球，1个红球，则白球概率为$\frac{99}{100}$，红球概率为$\frac{1}{100}$
  熵$H_2$
  $=\frac{1}{100}\ast lo{g}_{2}100+\frac{99}{100}\ast lo{g}_2\frac{100}{99}$
  $=\frac{1}{100}\ast lo{g}_{2}100+\frac{99}{100}\ast lo{g}_{2}100-\frac{99}{100}\ast lo{g}_{2}99$
  $=lo{g}_{2}100-\frac{99}{100}\ast lo{g}_{2}99\approx 0.080056$
  抽奖箱1号和抽奖箱2号的熵来看，H_2<H_1
  这意味着，抽奖箱1号的结果确定概率比较低，抽奖箱2号的确定性比较大
  从直觉上看，也是如此，抽奖箱2号，随便抽一个，有较大的可能性是白球，结果的确定性比较大
  但抽奖箱1号，随便抽一个，有可能是红橙黄绿青蓝紫金粉银种球的任意一种，不确定性较大

因此，鉴于熵、信息量N、事件量（实验量n)、事件概率P之间的关系，需要明确的就是：
熵表示结果确定时（可以是确定任一结果），所需的平均信息量

• 熵越大，事件结果的确定性越小（明确具体是哪个结果的确定性较小，分类越没把握）
• 熵越小，事件结果的确定性越大（明确具体是哪个结果的确定性较大，分类越有把握）

这里的信息熵，是根据分类结果，衡量系统分类的混乱情况

也就是，光看分类的结果，而不考虑特征等情况

就好比如说，只通过看一个班级的考试结果，来判断这个班的水平——只看结果
而不是根据这个班的特征，如教师水准、学生水平、教育资源等来判断这个班的水平——不看过程

但别忘了，决策树是根据特征进行分类的，因此分类结果的混乱情况，并不能说明决策树按特征分类的确定性很高。

所以，我们要时刻记住，决策树是根据特征来进行分类的，那么在选取哪个特征进行分类，才能使整体分类的确定性更高（也就是选取哪个特征进行分类，可以降低分类结果的不确定性）

目前，假设 Y 是分类结果，那么光是通过分类结果，来判断分类的不确定性，则是计算出 Y 的熵

$H(Y)=\Sigma P(y_i)lo{g}_2\frac{1}{P(y_i)}$——注意：这里的$y_i$指的是，第 i 种类别

这个H（Y）表示，当前系统的总体分类不确定性

那，根据哪个特征进行分类，可以减少总体系统的不确定性呢？
这个不确定性的减少是怎么衡量，如何计算的呢？

首先，用通俗的生活情况来理解：
假设我们目前只有性别的分类数据，男性占比60%，女性占比40%
那么，只根据分类结果来判断某个对象的类别时，分类的不确定性就是
$H（Y）=P_{男}lo{g}_2(\frac{1}{P_{男}})+P_{女}lo{g}_2(\frac{1}{P_{女}})$
但如果，我们根据某个特征，对这些分类结果，进行再一次分类，是不是能够减少分类的不确定性呢？
是的！
如果我们按是否有喉结，来对这些数据进行分类统计：

• 有喉结的男性占比：P(男|有喉结)
• 无喉结的男性占比：P(男|无喉结)
• 有喉结的女性占比：P(女|有喉结)
• 无喉结的女性占比：P(女|无喉结)
  会发现，根据喉结进行分类的数据，分类结果会更纯粹，也就是：有喉结基本都是男性，无喉结的基本都是女性
  那么，根据喉结这个特征进行分类，会使得分类结果的不确定性减少

这个不确定性的减少使怎么衡量，如何计算的呢？

这就要讲到 【条件熵】 了

1.3 条件熵

首先，假设我们先根据有无喉结这个特征，对数据进行分类统计：

• 有喉结的男性占比：P(男|有喉结)
• 无喉结的男性占比：P(男|无喉结)
• 有喉结的女性占比：P(女|有喉结)
• 无喉结的女性占比：P(女|无喉结)

根据有无喉结这个特征，进行分类后，分类结果确定时所需的平均信息量，也就是熵，我们称之为条件熵H(Y|X)
这个定义呢，呵呵，还是有点儿问题，不管它，后边再调整

这个条件熵，其实主要还是根据条件概率来计算的
信息熵公式：$H={\sum }_i{P}_i\ast N_i={\sum }_i{P}_i\ast lo{g}_2(\frac{1}{P_i})$
条件熵公式：$H(y|X)={\sum }_i{P}_{y|x_i}\ast N_{y|x_i}={\sum }_i{P}_{y|x_i}\ast lo{g}_2(\frac{1}{P_{y|x_i}})$
虽然，这个公式是有问题的，但先不管，按照常规思维先推下去
注意，这里的$x_i$，并不是第i个特征，而是某个特征x中的第几种特征值

类似于特征x假设是有无喉结，那么$x_0$可表示无喉结，$x_1$可表示有喉结，可以颠倒
只是想表达，$x_i$的意思

$H(y|X)$里的y，其实只表示了一种分类结果，而实际分类结果 Y，或许有多种类别
$Y:y_0,y_1,y_2...$

因此，完整的条件熵，应该是
$H(Y|X)=H(y_0|X)+H(y_1|X)+H(y_2|X)+....H(y_m|X)$

其中，X特征有 n 种特征值,Y有 m 种类别
$H(y_0|X)={\sum }_{i=1}^n{P}_{y_0|x_i}\ast lo{g}_2(\frac{1}{P_{y_0|x_i}})$
$H(y_1|X)={\sum }_{i=1}^n{P}_{y_1|x_i}\ast lo{g}_2(\frac{1}{P_{y_1|x_i}})$
…
$H(y_m|X)={\sum }_{i=1}^n{P}_{y_m|x_i}\ast lo{g}_2(\frac{1}{P_{y_m|x_i}})$

最终合并起来，就是
$H(Y|X)={\sum }_{j=1}^m{\sum }_{i=1}^n{P}_{y_j|x_i}\ast lo{g}_2(\frac{1}{P_{y_j|x_i}})$

看起来，好像合情合理
但是跟书本一对照，嗷~~~好像是很不对劲的！！！！
我在网上翻找一个知乎博主的解释，条件熵通俗解释
果然我原来的推导是真的不对劲…哈哈

重新理解一下，条件熵：Y的条件概率分布的熵的平均期望

这个课本的解释真是，让人毫无探索的欲望

分步理解吧，首先，什么是Y 的条件概率分布？
其实就是开头的统计分类：

• 有喉结的男性占比：P(男|有喉结)
• 无喉结的男性占比：P(男|无喉结)
• 有喉结的女性占比：P(女|有喉结)
• 无喉结的女性占比：P(女|无喉结)

那什么是Y的条件概率分布的熵呢？

其实就是根据特征分类后的熵

$H(Y|有喉结)=P_{（男|有喉结）}\ast lo{g}_2(\frac{1}{P_{（男|有喉结）}})+P_{（女|有喉结）}\ast lo{g}_2(\frac{1}{P_{（女|有喉结）}})$

$H(Y|无喉结)=P_{（男|无喉结）}\ast lo{g}_2(\frac{1}{P_{（男|无喉结）}})+P_{（女|无喉结）}\ast lo{g}_2(\frac{1}{P_{（女|无喉结）}})$

这就是根据特征分类后，分别得到的不同特征值的分类结果熵

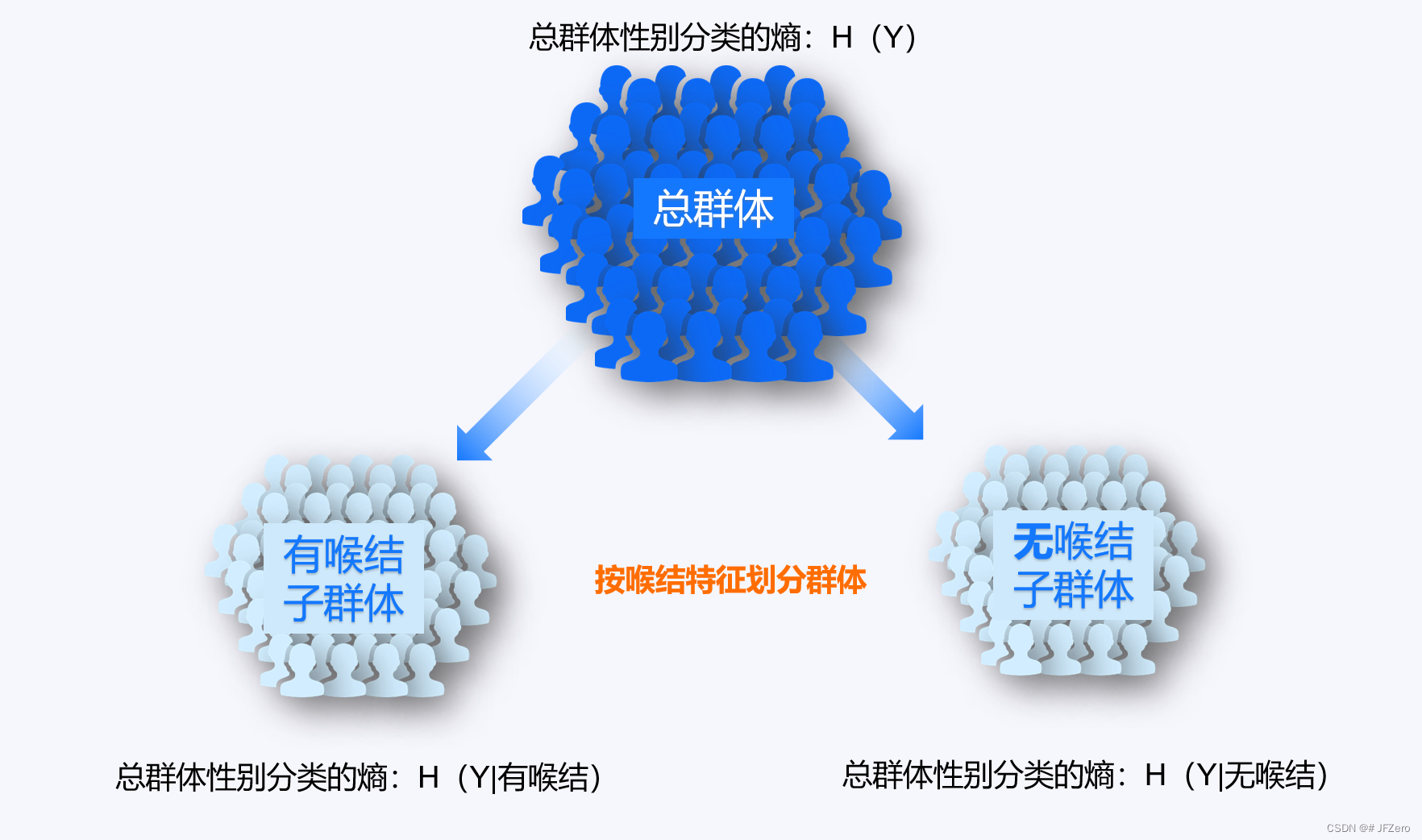
那按这个特征进行分类，就相当于一个大群体，分为了两个子群体

每个子群体分类结果确定时，都有各自子群体所需的平均信息量，即条件概率分布的熵

• 有喉结的对象为一个子群体，这个群体中分类结果确定时所需的平均信息量，即为熵$H(Y|有喉结)$
• 无喉结的对象为另一个子群体，这个群体中分类结果确定时所需的平均信息量，即为熵$H(Y|无喉结)$

那根据这个喉结特征分类时，所需的平均信息量，即为条件概率分布的熵的加权平均和

也就是$P(有喉结)H(Y|有喉结)+P(无喉结)H(Y|无喉结)$

这，正是条件熵！！！这下理解没错了吧…

所以条件熵的公式为
$H(Y|X)=P(有喉结)H(Y|有喉结)+P(无喉结)H(Y|无喉结)$

$P(有喉结)H(Y|有喉结)$
$=P(有喉结)[P_{（男|有喉结）}\ast lo{g}_2(\frac{1}{P_{（男|有喉结）}})+P_{（女|有喉结）}\ast lo{g}_2(\frac{1}{P_{（女|有喉结）}})]$

$P(无喉结)H(Y|无喉结)$
$=P(无喉结)[P_{（男|无喉结）}\ast lo{g}_2(\frac{1}{P_{（男|无喉结）}})+P_{（女|无喉结）}\ast lo{g}_2(\frac{1}{P_{（女|无喉结）}})]$

实际，也就是先算出每个特征值下的条件概率的熵，如下：
$H(Y|x_1)={\sum }_{i=1}^m{P}_{(y_i|x_1)}\ast lo{g}_2(\frac{1}{P_{(y_i|x_1)}})$
$H(Y|x_2)={\sum }_{i=1}^m{P}_{(y_i|x_2)}\ast lo{g}_2(\frac{1}{P_{(y_i|x_2)}})$
…
$H(Y|x_n)={\sum }_{i=1}^m{P}_{(y_i|x_n)}\ast lo{g}_2(\frac{1}{P_{(y_i|x_n)}})$
再计算出每个特征值下的条件概率的熵的加权平均和，其实就是条件熵
$H(Y|X)=P(x_1)H(Y|x_1)+P(x_2)H(Y|x_2)+...+P(x_n)H(Y|x_n)$

$={\sum }_{j=1}^{n}P(x_j){\sum }_{i=1}^m{P}_{(y_i|x_j)}\ast lo{g}_2(\frac{1}{P_{(y_i|x_j)}})$

以上就是条件熵的分布及含义

条件熵，表示按照某个特征分为几个子群体后，各子群体的信息熵的平均信息熵。

按道理来说，我们在决策树中，选取某个特征进行划分群体时，应选择那个能使条件熵最小的那个特征
也就是：先计算所有特征对应的条件熵，选出条件熵最小的那个特征进行分类
这样就能保证了分类结果的确定性更高

但不知道为什么，还要提出信息增益

1.4 信息增益

信息增益，表示按该特征划分群体后，使得群体分类的确定性增加的程度，也就是减少了多少不确定性。

$Gain=H（Y）-H（Y|X)$
$信息增益=总熵-条件熵$

总熵固定的情况下，条件熵越小，信息增益越大，表示按照该特征分类，会带来更多的信息量，大大减少不确定性

说实话，我觉得信息增益这么个东西，其实有些扰乱逻辑，完全没必要
这就好像是，现在要对比哪个策略更能减少错误，我们分别计算出各个策略下的错误量（条件熵），只要横向比较各个策略哪个错误两更小，就表示该策略效果更好——这样就很简单
但信息增益这个东西，就像是gain = 【原本无策略下的总错误量-策略下的错误量】，再进行横向比较各个策略下的gain：如果gain越大，则策略表现越好（可以较大程度地减少错误量），逻辑没问题，但有什么必要呢

信息增益无非是一种正向线性思维逻辑：gain越大，特征划分表现越好；gain越小，特征划分表现越差
条件熵则是一种反向线性思维逻辑：条件熵越小，特征划分表现越好；条件熵越大，特征划分表现越差

但条件熵的逻辑表述…显然更押韵…小-好，大-差…
押韵的东西，天然美好

但为什么信息增益又不够好呢？为什么人们又提出了信息增益率呢？

书上说，信息增益对那些特征值比较多的特征有所偏好，也就是说，采用信息增益作为判定方法，会倾向于去选择特征值比较多的特征。
哦？为什么信息增益对那些特征值比较多的特征有所偏好呢？

这就要回到信息增益的公式上看，首先总熵H（Y）是固定不变的，那就是条件熵尽可能小，才会选择该特征
$Gain=H（Y）-H（Y|X)$

因此，信息增益的缺陷是：信息增益对特征值特别多的特征有所偏好，换句话说就是，特征值特别多的特征，通常计算出的条件熵都比较小

哦？why？进一步拆解条件熵的公式

$H(Y|X)=P(x_1)H(Y|x_1)+P(x_2)H(Y|x_2)+...+P(x_n)H(Y|x_n)$
现在要分析，为什么x的取值越多，H(Y|X)越小？

首先，可以想象一个极端的场景，如果某个特征，可以把总群体分为100个子群体，每个子群体里只有2个对象，那么，每个>子群体的分类确定性很高，有些子群体的熵为0，有些子群体的熵为3（或更大）。

• 但由于子群体的概率$P（x_n)$相对较小，因此当子群体的熵较大时，P较小，最终累计的加权平均值条件熵H（Y|X)也是相对比较小的。

另外一个特征，可以把总群体分为2个子群体，每个子群体里有50个对象，那么每个子群体极有可能不会特别的纯粹，那么子群体的熵就相对大一些。

• 并且由于子群体的概率$P（x_n)$相对较大，子群体的熵较大时，最终累计的加权平均值条件熵H（Y|X)也会相对较大

以上是基于现实经验的分析得到的结论，但实际是可以通过数学层面来分析的

这种情况下，特征值较多的特征，条件熵普遍较小，因此基于信息增益来选取特征划分群体时，往往选到的都是特征值多的特征。

为什么不应该选特征值多的特征来划分群体呢？

因为容易过拟合，同时，由于特征值较多的情况下，就会分为更多的子群体，这有可能导致每个群体的对象数量比较少，对象数量较少的情况下进行分类，容易出现分类错误的情况

假设全班身高2.2米的人也就那么2个，这个子群体对象数量太少了，不宜根据对象类别进行分类

• 例如：假设这2 个人都是女生，那么当某个人是2.3米身高时，根据身高特征划分为2.2米以上群体时，有2个历史数据显示都是女生，因此判定2.3米的这个人也是女生——这显然是不合理的

特征值太多，容易过拟合

既然信息增益，容易受特征值较多的干扰，那就想办法剔除或弱化这样的干扰。

怎么剔除呢？

我们知道，特征值较多，容易导致划分的各子群熵较小，各子群的概率也较小，最终使各子群的加群平均和——划分子群体越多：条件熵较小，信息增益较大。

但划分的子群体越多，各子群体构成的熵是多大的。这样的逻辑，放在分类上也是一样的，如果不考虑特征，总群体的分类本来就比较多，那么各类别的子群体，概率较小，总体的熵是比较大的。

这就要从熵的公式来看
$H={\sum }_i{P}_i\ast N_i={\sum }_i{P}_i\ast lo{g}_2(\frac{1}{P_i})$

变换一下：$H=P_1\ast lo{g}_2(\frac{1}{P_1})+P_2\ast lo{g}_2(\frac{1}{P_2})+P_3\ast lo{g}_2(\frac{1}{P_3})+....$

假设各类别的概率P值都一样，也就是各类别占比一样，那么我们对比不同的类别数，看看熵的大小对比
假设有3种类别，每种类别概率P相同，均为1/3：

• $H={\sum }_i{P}_i\ast lo{g}_2(\frac{1}{P_i})=3\ast P\ast lo{g}_2(\frac{1}{P})=lo{g}_2(3)$

假设有100种类别，每种类别概率P相同，均为1/100：

• $H={\sum }_i{P}_i\ast lo{g}_2(\frac{1}{P_i})=100\ast P\ast lo{g}_2(\frac{1}{P})=lo{g}_2(100)$

现在，我们不是以类别分群体来计算熵了，我们以特征划分群体，来计算熵（不是条件熵）

$H(X)={\sum }_{x_i}^n{P}_{x_i}\ast N_i={\sum }_{x_i}^n{P}_{x_i}\ast lo{g}_2(\frac{1}{P_{x_i}})$

当特征划分的群体越多（n越大），则特征群体的熵H（X）也越大。

因此，我们可以用信息增益Gain ÷ 特征群体的熵H（X)，这样由于特征多的影响，就在一定程度上抵消了。

因为信息增益Gain与特征群体的熵H（X），都是会因为特征值的增多而增大，那么两两相比，就可以在一定程度上消除特征值增多带来的影响。

这就好像，假设对比两个人谁更重，我们考虑由于吃饭会导致体重在某一瞬间增加，因此我们计划剔除掉吃饭带来的体重增加影响
首先我们知道，吃越多饭，会使体重增加的越多，同时吃越多饭，流越多汗
如果我们无法统计出饭量，那可以统计出汗量
那我们可以用体重除以汗量，来消除吃饭带来的体重增加影响
em。。。感觉不太对劲

不管了

而信息增益与特征群体的熵的比值，就是信息增益率
$Gain\_rate=\frac{Gain}{H(X)}$

聊聊基尼系数，基尼系数是第三种用于衡量按某个特征分类，是否确定性更高的指标。

1.5 基尼系数

基尼系数，更准确地说，其实应该叫做基尼杂质系数

它跟用于衡量国家贫富差距的经济指标基尼系数，不是一回事！！！
当初由于不理解基尼系数，还专门去学习了经济指标基尼系数，最后发现，好像不是一回事
越学越懵，以至于我对决策树，产生一种厌恶…畏难情绪滋生导致的

首先，经过各大up主苦心孤诣地分享自己的理解，我发现基尼杂质系数呢，原理其实很简单

基尼杂质系数，其实就是决策树分类的平均错误率

首先，先不讲按特征分类的情况，先直接看分类结果。

假设总群体里，有 3 个A，3个B，6个C，总共12个对象，3个类别

那么每个对象的分类错误率分别是多少呢？
一个A对象，分类错误就是分为了B或C，B或C的占比则是它的分类错误率，即$\frac{12-3}{12}=\frac{9}{12}$
第2个A对象，分类错误率也是$\frac{9}{12}$,第3个A对象，分类错误率也是一样的

一个B对象，分类错误，则是分为了A或C，因此分类错误率是$\frac{9}{12}$
另外两个B对象，分类错误率也是一样的$\frac{9}{12}$

一个C对象，分类错误率同理可推出是$\frac{6}{12}$
其余的C对象，分类错误率也是一样的$\frac{6}{12}$

那么这个群体里，总的分类错误率为$3\ast \frac{9}{12}+3\ast \frac{9}{12}+6\ast \frac{6}{12}$
那么，这个群体的平均分类错误率为
$\frac{3\ast \frac{9}{12}+3\ast \frac{9}{12}+6\ast \frac{6}{12}}{12}=\frac{3}{12}\ast \frac{9}{12}+\frac{3}{12}\ast \frac{9}{12}+\frac{6}{12}\ast \frac{6}{12}$

$=\frac{3}{12}\ast (1-\frac{3}{12})+\frac{3}{12}\ast (1-\frac{3}{12})+\frac{6}{12}\ast (1-\frac{6}{12})$

这就是基尼系数的计算公式，我们抽象如下
$Gini=\Sigma P(1-P)$

以上，是未按特征分类时的Gini系数，但现在要衡量按某个特征分类后，分类结果确定性的大小，那就是对特征划分多个子群体的Gini系数，进行加权求和。（类似于条件熵）

先计算出按特征划分出的多个子群体的Gini系数

$Gini(Y|x_1)={\sum }_{i=1}^m{P}_{(y_i|x_1)}\ast (1-P_{(y_i|x_1)})$
$Gini(Y|x_2)={\sum }_{i=1}^m{P}_{(y_i|x_2)}\ast (1-P_{(y_i|x_2)})$
…
$Gini(Y|x_n)={\sum }_{i=1}^m{P}_{(y_i|x_n)}\ast (1-P_{(y_i|x_n)})$

再基于各子群体的比率，对这些基尼系数进行加权求和，得到最终的基尼系数

$Gini=P(x_1)Gini(Y|x_1)+P(x_1)Gini(Y|x_2)+...+P(x_n)Gini(Y|x_n)$

这个过程跟条件熵其实很像很像很像，计算逻辑是一样的，只不过指标选取不同罢了

但基尼系数，是否会因为特征值的增多，而导致基尼系数有所改变呢？

其实一定是有的

你比如说特征值特别多的情况下，各子群分类会比较纯，则子群的基尼系数P*(1-P)会非常小，且各子群的占比也比较小，那么总体的加权平均和——基尼系数也就更小。

因此，如果应用基尼系数作为衡量特征选择的指标，那么基尼系数也会和条件熵一样，选择特征值较多的指标，这样就容易出现过拟合。

因此，我们应当对特征值的数量进行一个惩罚。

这是我的想当然，但我发现课本上。。。只用了基尼系数作为衡量。。。em。。。。

或许至少应该要基尼系数增益去衡量吧。。。但显然有些书也没讲

我想象中的基尼系数增益：总群体的基尼系数 - 按特征分类后的基尼系数

我想象中的基尼系数增益率：$\frac{基尼系数增益率}{按特征划分多个群体的基尼系数加权平均}$

不知道其他书有没有特别讲，回头我用程序试试看。

nice，讲到这里，我认为我对决策树的特征选择三种决策原理，已经理解的透透的了！！！
真不容易啊，果然还是要文字梳理出来，才能理解
还要自己举例，才知道怎么回事
还要自己打脸，诚恳地低下无知的头颅，只是为了更好锻炼颈椎
nice

2. 总结

• 信息增益：ID3算法
• 信息增益率：C4.5算法
• 基尼系数：CART算法

为什么叫这些名？不懂。。。不重要。。。