以二元一次方程组的求解为例:
{ a c a 1 + b c b 1 = c 1 a c a 2 + b c b 2 = c 2 \left\{\begin{array}{l} a_{c}a_{1} +b_{c}b_{1} =c_{1} \\ a_{c}a_{2} +b_cb_{2} =c_{2} \end{array}\right. {aca1+bcb1=c1aca2+bcb2=c2
其中 a c a_c ac和 b c b_c bc是我们待求的参数。
求解克莱姆法则为:
a c = c 1 b 2 − c 2 b 1 a 1 b 2 − a 2 b 1 = ∣ c 1 b 1 c 2 b 2 ∣ ∣ a 1 b 1 a 2 b 2 ∣ = ∣ c b ∣ ∣ a b ∣ a_{c}=\frac{c_{1} b_{2}-c_{2} b_{1}}{a_{1} b_{2}-a_{2} b_{1}}=\frac{\left|\begin{array}{ll} c_{1} & b_{1} \\ c_{2} & b_{2} \end{array}\right|}{\left|\begin{array}{ll} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array}\right|}=\frac{|\mathbf{cb}|}{|\mathbf{ab}|} ac=a1b2−a2b1c1b2−c2b1= a1a2b1b2 c1c2b1b2 =∣ab∣∣cb∣
b c = a 1 c 2 − a 2 c 1 a 1 b 2 − a 2 b 1 = ∣ a 1 c 1 a 2 c 2 ∣ ∣ a 1 b 1 a 2 b 2 ∣ = ∣ a c ∣ ∣ a b ∣ b_{c}=\frac{a_{1} c_{2}-a_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}=\frac{\left|\begin{array}{ll} a_{1} & c_{1} \\ a_{2} & c_{2} \end{array}\right|}{\left|\begin{array}{ll} a_{1} & b_{1} \\ a_{2} & b_{2} \end{array}\right|}=\frac{|\mathbf{ac}|}{|\mathbf{ab}|} bc=a1b2−a2b1a1c2−a2c1= a1a2b1b2 a1a2c1c2 =∣ab∣∣ac∣
注意上面我们把行列式每一列都写成列向量的形式,也即
a = ( a 1 a 2 ) , b = ( b 1 b 2 ) , c = ( c 1 c 2 ) \mathbf{a}=\begin{pmatrix}a_1\\a_2\end{pmatrix}, \mathbf{b}=\begin{pmatrix}b_1\\b_2\end{pmatrix}, \mathbf{c}=\begin{pmatrix}c_1\\c_2\end{pmatrix} a=(a1a2),b=(b1b2),c=(c1c2)
上面的方程则改写为:
a c a + b c b = c a_{c}\mathbf{a}+b_{c} \mathbf{b}=\mathbf{c} aca+bcb=c
我们不妨从几何直观来看:
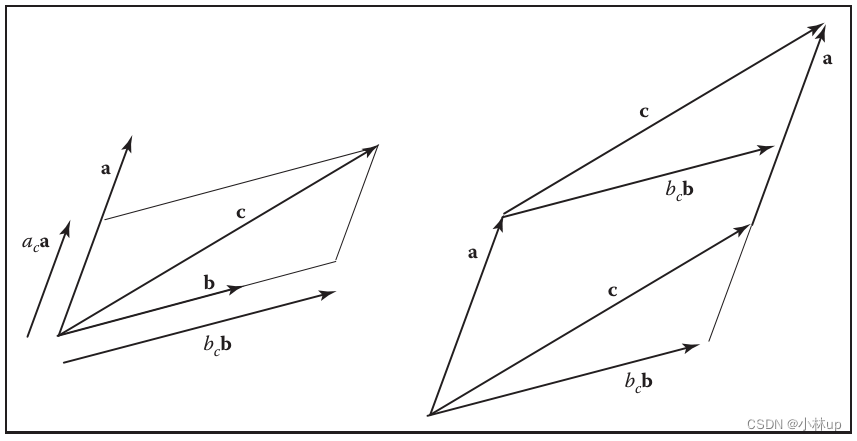
从这个图我们发现【 ( b c b ) (b_c\mathbf{b}) (bcb)和 a \mathbf a a围成的平行四边形面积】和【 c \mathbf{c} c和 a \mathbf a a围成的平行四边形面积】相等(这里用到了行列式的几何意义,在我的这篇博客里有叙述:线性代数行列式的几何含义。)。
∣ ( b c b ) a ∣ = ∣ c a ∣ \left|\left(b_{c} \mathbf{b}\right) \mathbf{a}\right|=|\mathbf{c a}| ∣(bcb)a∣=∣ca∣
b c b_c bc是常数,我们可以提取出来:
于是就有了克莱姆法则:
b c = ∣ c a ∣ ∣ b a ∣ a c = ∣ b c ∣ ∣ b a ∣ b_{c}=\frac{|\mathbf{c a}|}{|\mathbf{b a}|}\\a_{c}=\frac{|\mathbf{b c}|}{|\mathbf{b a}|} bc=∣ba∣∣ca∣ac=∣ba∣∣bc∣







![[nexus]基于nexus搭建npm仓库及上传插件到仓库](https://img-blog.csdnimg.cn/b796514ea10242cfb2c885c26adb2b52.png)