概要

     所有模数转换器(ADC)都有一定量的“折合到输入端噪声”，可以将其模拟为与无噪声 ADC 输入串联的噪声源。折合到输入端噪声与量化噪声不同，后者仅在 ADC 处理交流 信号时出现。多数情况下，输入噪声越低越好，但在某些情况下，输入噪声实际上有 助于实现更高的分辨率。这似乎毫无道理，不过继续阅读本指南，就会明白为什么有 些噪声是好的噪声。

整体架构流程

提示：这里可以添加技术整体架构

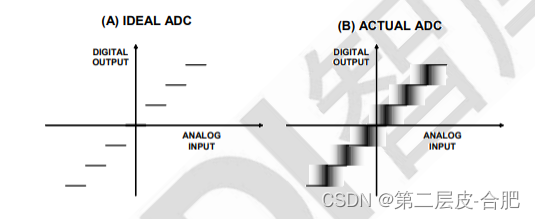
     实际的 ADC 在许多方面与理想的 ADC 有偏差。折合到输入端的噪声肯定不是理想情 况下会出现的，它对 ADC 整体传递函数的影响如图 所示。随着模拟输入电压提高， “理想”ADC（如图  所示）保持恒定的输出代码，直至达到跃迁区，此时输出代码 即刻跳变为下一个值，并且保持该值，直至达到下一个跃迁区。理论上，理想 ADC 的 “代码跃迁”噪声为 0，跃迁区宽度也等于 0。实际的 ADC 具有一定量的代码跃迁噪 声，因此跃迁区宽度取决于折合到输入端噪声的量（如图 所示）。图 显示的情 况是代码跃迁噪声的宽度约为 1 个 LSB（最低有效位）峰峰值。 

 

 

技术名词解释

提示：这里可以添加技术名词解释

例如：

• Bert
• GPT 初代
• GPT-2
• GPT-3
• ChatGPT

技术细节

提示：这里可以添加技术细节

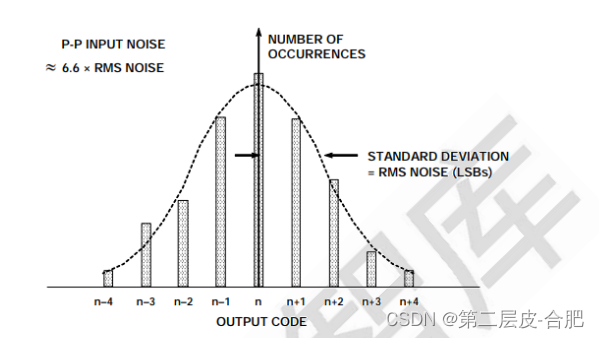
    由于电阻噪声和“kT/C”噪声，所有 ADC 内部电路都会产生一定量的均方根(RMS)噪 声。即使是直流输入信号，此噪声也存在，它是代码跃迁噪声存在的原因。如今通常 把代码跃迁噪声称为“折合到输入端噪声”，而不是直接使用“代码跃迁噪声”这一 说法。折合到输入端噪声通常用 ADC 输入为直流值时的若干输出样本的直方图来表 征。大多数高速或高分辨率 ADC 的输出为一系列以直流输入标称值为中心的代码（见 图 2）。为了测量其值，ADC 的输入端接地或连接到一个深度去耦的电压源，然后采 集大量输出样本并将其表示为直方图（有时也称为“接地输入”直方图）。由于噪声 大致呈高斯分布，因此可以计算直方图的标准差 σ，它对应于有效输入均方根噪声

 

 

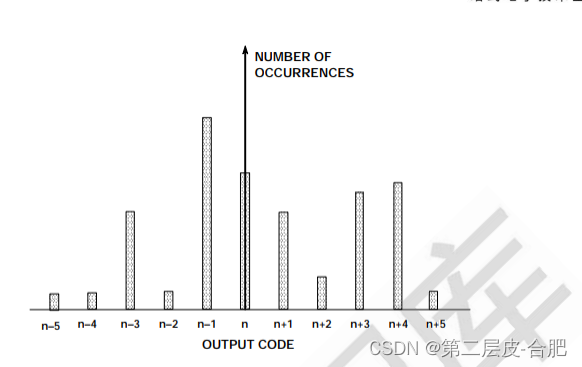
虽然 ADC 固有的微分非线性(DNL)可能会导致其噪声分布与理想的高斯分布有细微的 偏差（图  示例中显示了部分 DNL），但它至少大致呈高斯分布。如果 DNL 比较大， 则应计算多个不同直流输入电压的 σ 值，然后求平均值。例如，如果代码分布具有较 大且独特的峰值和谷值，则表明 ADC 设计不佳，或者更有可能的是 PCB 布局布线错 误、接地不良、电源去耦不当（）。当直流输入扫过 ADC 输入电压范围时，如 果分布宽度急剧变化，这也表明存在问题

    ADC 的无噪声代码分辨率是指这样一个位数，如果超过该位数，则无法明确无误地解 析各个代码，原因是存在所有 ADC 都具有的有效输入噪声（或折合到输入端噪声）， 如上文所述。该噪声可以表示为均方根量，单位通常是 LSBrms。乘以系数 6.6 可以 将均方根噪声转换为峰峰值噪声（用“LSB 峰峰值”表示）。N 位 ADC 的总范围为 2 NLSB。因此，无噪声采样总数等于： 

 

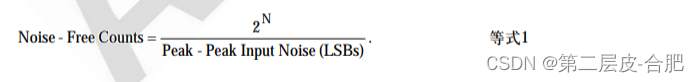
 注意，当输出数据速率为 50Hz、输入范围为±10mV 时，无噪声代码分辨率为 16.5 位 （80,000 无噪声采样）。这些条件下的建立时间为 460ms，因此该 ADC 是精密电子 秤应用的理想之选。对于适合精密测量应用的高分辨率 Σ-Δ 型 ADC，大部分数据手册 都提供了类似的数据。 有时候会利用满量程范围与均方根输入噪声（而非峰峰值噪声）的比值来计算分辨率， 该分辨率称为“有效分辨率”。注意：在相同条件下，有效分辨率比无噪声代码分辨 率高 log2(6.6)，约 2.7 位。

 

 

小结

提示：这里可以添加总结

例如：

     现在考虑这样一种情况：ADC 的折合到输入端噪声非常低，直方图总是显示一个明确 的代码，对于这种 ADC，数字均值有何作用呢？答案很简单——没有作用！无论对多少 样本进行平均，答案始终相同。但只要将足够大的噪声增加到输入信号中，使得直方 图中有一个以上的代码，那么均值方法又会发挥效用。因此，少量噪声可能是好事情 （至少对于均值方法而言），但输入端存在的噪声越高，为实现相同分辨率所需的均 值样本数越多。