题目描述：下载附件后，附件中只有两个文件，一个是加密后的密钥，一个是公钥文件

背景知识：RSA加密算法

 现在相当于给出了密文和公钥，需要我们去求解明文

1. 思路分析

既然要解密，那么必须要获取私钥；

现在只有公钥，即只知道e和n，现在要想获取到私钥，那么不可避免的需要对n进行分解获取到p和q

分解到p和q后，计算出私钥，然后对密文进行解密即可

这个过程手工计算比较麻烦，整个过程主要利用一些工具进行操作，详细过程见第二步骤

2. 解题过程

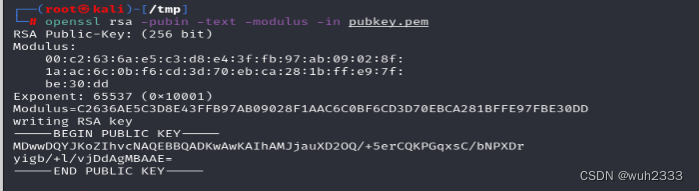
2.1 利用openssl工具分解出e和modulus（这里应该就是那个n）

命令为：openssl rsa -pubin -text -modulus -in pubkey.pem

其中-pubin表示指定输入文件为公钥，-text表示以文本形式输出，-modulus表示输出模数值，-in表示输入文件。其余参数可以通过命令openssl rsa -help查看，这里就不赘述了。

2.2 利用进制转换工具将16进制转换为10进制

这里直接在网上搜索即可，这里我用的在线工具进制转换 - 在线工具

我们需要将modulus（n）转成10进制，转换后的结果为：87924348264132406875276140514499937145050893665602592992418171647042491658461

 2.3 分解该modulus（n）

在线网站：factordb.com 对modulus（n）进行分解，计算出p, q

 

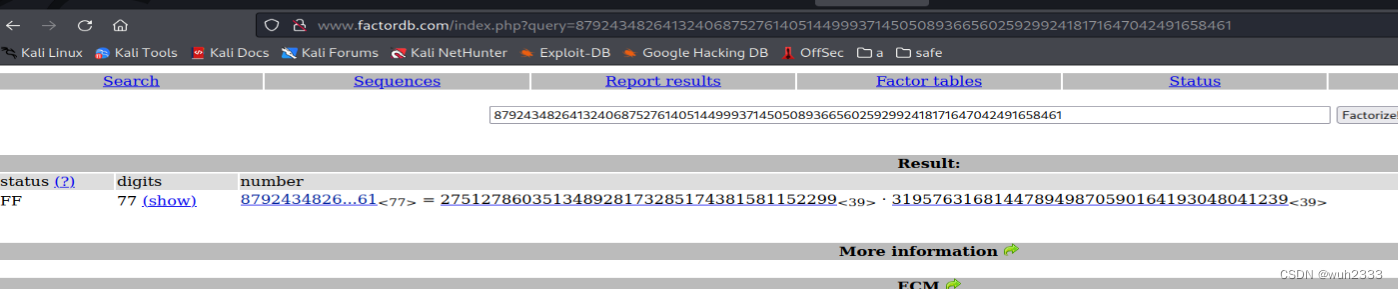
p = 275127860351348928173285174381581152299 

q = 319576316814478949870590164193048041239

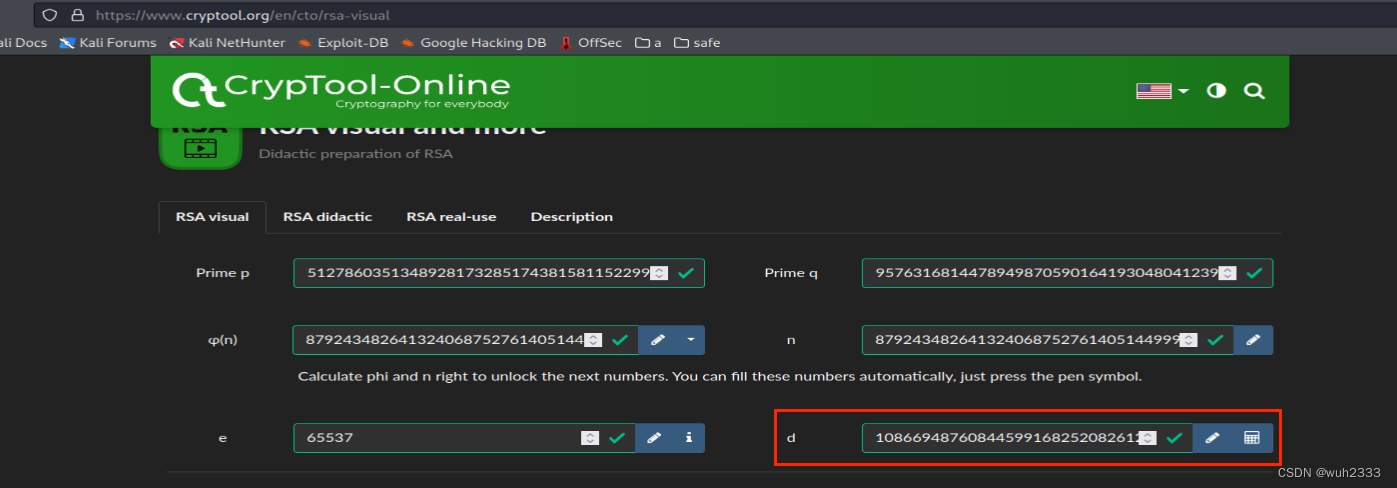
2.4 计算出私钥

结合前面的 e = 65537和p, q两个值，这里可以利用在线工具（这一步非必须，只是有介绍下这个工具）RSA visual and more - CrypTool Portal计算出了d的值为10866948760844599168252082612378495977388271279679231539839049698621994994673

生成私钥文件，这里使用rsatool工具来生成

工具安装命令：

git clone https://github.com/ius/rsatool.git
cd rsatool
python setup.py install

安装好后，执行命令：python rsatool.py -o private.pem -e 65537 -p 275127860351348928173285174381581152299  -q 319576316814478949870590164193048041239

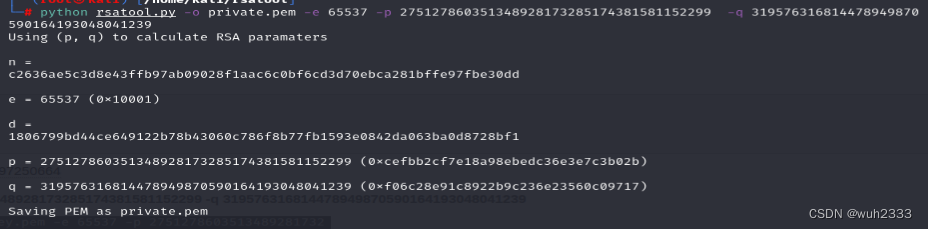
 此时生成私钥文件private.pem

2.5 解密

 生成私钥文件后，使用openssl解密即可

openssl rsautl -decrypt -in flag.enc -inkey private.pem

其中-decrypt表示解密，-in表示输入的加密文件，-inkey表示输入的密钥

获取到flag为PCTF{256b_i5_m3dium}

 

总结：这个也是RSA算法的解密过程，这个过程如果使用人工计算，或者手动编程计算都比较难，因此，工具的利用就非常重要了，这里主要是用了三个工具：openssl/在线进制转换/rsatool工具，利用这些工具可以极大提升我们的效率