Ⅰ.知前序和中序推理后序

题目名称：
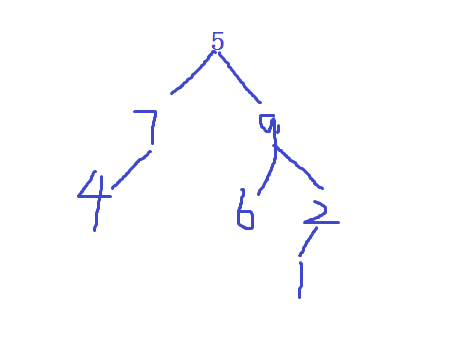
1.已知某二叉树的前序遍历序列为5 7 4 9 6 2 1，中序遍历序列为4 7 5 6 9 1 2，则其后序遍历序列为（ C）

题目内容：
A .4 2 5 7 6 9 1
B .4 2 7 5 6 9 1
C .4 7 6 1 2 9 5
D .4 7 2 9 5 6 1

这类题其实很简单，就是根据前序/后序的排列，和中序的特性来推理。
中序的特性就是先遍历左子树，再遍历根，最后遍历右子树。也就是说根的左边和右边分别是左子树和右子树。
前序遍历的特性是先遍历根，再遍历左右子树，所以第一个就是根。也就是5是根，那么对应中序中的5左右分别是左子树和右子树(5的左边是4 7 ，5的右边是6 9 1 2)。

而左右子树分别又是一颗树。我们就可以将前序和中序中的5给划掉，那么前序中第一个就变成7了，7就是对应的左子树了。而7再对应中序中左边是4右边没有，说明根7的左子树是4没有右子树。然后就可以将7和4给划去了。再看前序中的9就是5的右子树了。而9对应的中序中左边是6，右边是1 2，所以9的左子树是6右子树是1和2中的一个。然后将6 9 划去，前序中剩下的就是2了，那么2就是9的右子树。2对应的中序中左边是1，所以2的左子树是1，右边没有，所以没有右子树。

题目名称：
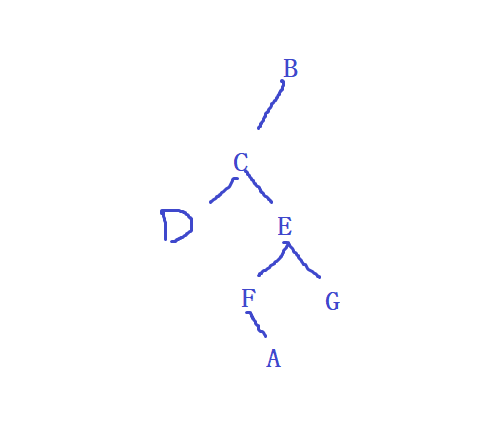
2.已知二叉树的前序序列为BCDEFAG，中序序列为DCFAEGB，请问后序序列为__C_
A. DAFEGCB
B. DAEGFCB
C. DAFGECB
D. DAEFGCB

根据前序遍历和中序遍历来推理后序遍历。跟第一题是一样的。
前序第一个就是根，然后再对应中序找到根的左右子树。
B是根，中序中B在最后面，说明根只有左子树，没有右子树。然后将B划去。
接下来就是C，也就是C是B的左子树。再对应于中序中C的左边是D右边是FAEGB。
说明C的左子树是D右子树不确定。可以将C和D给划去。
前序第一个就是E，所以E是C的右子树。对应于中序E的左边是FA右边是G。左子树和右子树不确定。接着看。
划去E后，前序第一个就是F说明E的左子树是F。对应中序F的右边是A左边没有说明F的右子树是A。没有左子树。划去FA，前序就剩G了，说明G是E的右子树。

题目名称：
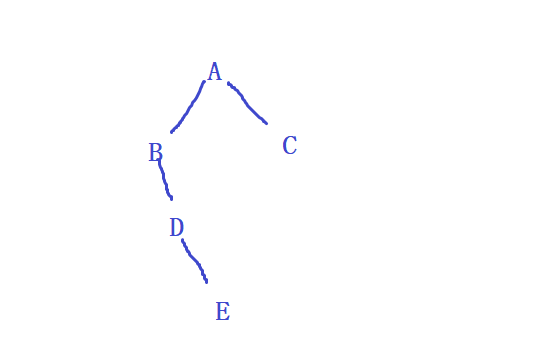
3.已知某二叉树的前序遍历序列为ABDEC，中序遍历序列为BDEAC，则该二叉树（C ）

题目内容：
A .是满二叉树
B .是完全二叉树，不是满二叉树
C .不是完全二叉树
D .是所有的结点都没有右子树的二叉树

与第一题和第二题本质一样，就是根据前序遍历和中序遍历来画出二叉树。
前序第一个是A，所以根是A。中序中A的左边是BDE右边是C。所以A的右子树是C，左子树不确定。
划去A和C后，前序中第一个是B，所以B是A的左子树。再看中序中B的左边没有右边是DE所以B没有左子树，右子树不确定，划去B，前序中就剩E，所以B的右子树是E。

Ⅱ.知后序和中序推理前序

第 1题（单选题）
题目名称：
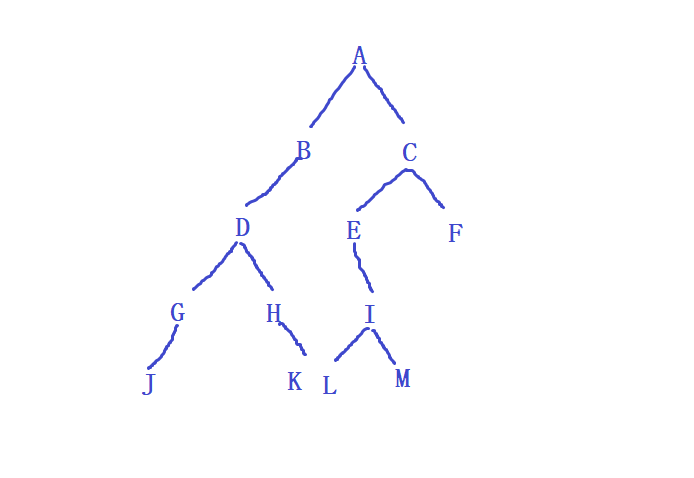
已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（B ）

题目内容：
A .ABDGHJKCEFILM
B .ABDGJHKCEILMF
C .ABDHKGJCEILMF
D .ABDGJHKCEIMLF

这里和知道前序和中序来推理后序是本质一样的。只不过前序遍历先遍历根节点。后序遍历最后才遍历根节点。
也就是后序遍历最后一个才是根，前面的是右节点，再前面的是左节点。
所以跟上面类似，先找到根节点，然后到中序中找根节点的左右节点。
后序中最后一个是A，所以根是A，对应中序中来看，A的左边是左子树，右边是右子树。
划去A，那么后序中最后一个就是C了，C就是A的右子树(因为C在A的右边),对应中序C的右边是右子树，左边是左子树。所以F是C的右子树。划去C，F。后序最后一个是E，所以E就是C的左子树。对应中序E的左边是左子树，右边没有，所以没有右子树。划去E，后序最后一个是I，I就是E的左子树，对应中序E的左边…………就按照这样的方法来一一对应即可。

Ⅲ.深度/广度遍历

题目名称：
1.二叉树的( 层序)遍历相当于广度优先遍历，(前序 )遍历相当于深度优先遍历

题目内容：
A .前序中序
B .中序前序
C .层序后序
D .层序前序

1.广度优先遍历会把下一步所有的位置全部遍历完，才会进行更深层次的遍历，层序遍历就是一种广度优先遍历。
2.深度优先遍历是先遍历完一条完整的路径(从根到叶子的完整路径)才会向上层折返，再去遍历下一个路径，前序遍历就是一种深度优先遍历。

Ⅳ.通过遍历推理树的形状

题目名称：
1.如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（B ）种

题目内容：
A .13
B .14
C .15
D .16

这颗二叉树要么是三层要么是四层，在3~4层之间。
但能确定的是A是根结点。所以我们来分类讨论一下，当这个二叉树是三层时。
左子树存在：A(B,C(D,)) A(B,C(,D)) A(B(C,),D) A(B(,C),D) A(B(C,D))
左子树不存在：A(,B(C,D)) A) A(,B(C(D)))
当这个二叉树是四层时
那么这个二叉树肯定是单边树。除第一个A能确定外，其余三个每个结点都有两种选择(左或右),所以有222=8种，加起来就是14种。

题目名称：
2.一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满足（C ）

题目内容：
A .所有的结点均无左孩子
B .所有的结点均无右孩子
C .只有一个叶子结点
D .至多只有一个结点