一:分类方法
(一)逻辑回归
最简单的方法就是将分类问题视为回归问题,采用逻辑回归计算分类的边界。
(二)softmax回归
softmax的前向传播过程可以分为以下三步:
h
=
W
T
x
y
^
=
s
o
f
t
m
a
x
(
h
)
l
o
s
s
=
−
y
l
o
g
y
^
h= W^Tx\\ \hat y=softmax(h)\\ loss=-y\ log\ \hat y
h=WTxy^=softmax(h)loss=−y log y^
(1)第一步:
h
=
W
T
x
h= W^Tx
h=WTx
W T W^T WT是一个 m ∗ n m*n m∗n的矩阵,其中 m m m是分类的数目, n n n是 x x x的维度;
x x x是一个 n n n维向量,是模型的输入;
将二者进行矩阵乘法,得到一个 m m m维输出 h h h。
h h h代表了我们进行 m m m元分类的结果,此时模型给出的每个类的得分并未进行归一化(就是概率加和不为 1 1 1)。
(2)第二步: y ^ = s o f t m a x ( h ) \hat y=softmax(h) y^=softmax(h)
对第一步未进行归一化的结果 h h h进行归一化处理。
(3)第三步: l o s s = − y l o g y ^ loss=-y\ log\ \hat y loss=−y log y^
采用交叉熵损失作为损失函数,对目标概率分布与模型概率分布之间的差距进行评估。
这一操作类似于将 [ 0 , 0 , 0 , 1 , 0 ] T [0,0,0,1,0]^T [0,0,0,1,0]T与 y ^ \hat y y^进行矩阵乘法,乘积得到的结果是模型为正确类给出的得分。
我们希望这一得分尽可能的大,也就是说,我们希望最后的输出中,得分最高的一类就是正确的分类结果。
最后可以得到损失函数:
J
(
θ
)
=
1
N
∑
i
=
1
N
−
y
i
l
o
g
y
^
i
=
1
N
∑
i
=
1
N
−
y
i
l
o
g
s
o
f
t
m
a
x
(
h
i
)
=
1
N
∑
i
=
1
N
−
y
i
l
o
g
e
h
i
∑
c
=
1
C
e
h
c
=
1
N
∑
i
=
1
N
−
y
i
l
o
g
e
W
T
x
i
∑
c
=
1
C
e
W
T
h
c
\begin{aligned} J(\theta)&=\frac1N\sum^N_{i=1}-y_i\ log\ \hat y_i\\ &=\frac1N\sum^N_{i=1}-y_i\ log\ softmax(h_i)\\ &=\frac1N\sum^N_{i=1}-y_i\ log\ \frac{e^{h_i}}{\sum^C_{c=1} e^{h_c}}\\ &=\frac1N\sum^N_{i=1}-y_i\ log\ \frac{e^{W^Tx_i}}{\sum^C_{c=1} e^{W^Th_c}} \end{aligned}
J(θ)=N1i=1∑N−yi log y^i=N1i=1∑N−yi log softmax(hi)=N1i=1∑N−yi log ∑c=1Cehcehi=N1i=1∑N−yi log ∑c=1CeWThceWTxi
这里我们采用权重衰减进行正则化,防止模型过拟合。
J
(
θ
)
=
=
1
N
∑
i
=
1
N
−
y
i
l
o
g
e
W
T
x
i
∑
c
=
1
C
e
W
T
h
c
+
λ
∑
k
θ
k
2
J(\theta)==\frac1N\sum^N_{i=1}-y_i\ log\ \frac{e^{W^Tx_i}}{\sum^C_{c=1} e^{W^Th_c}}+\lambda\sum_k\theta_k^2
J(θ)==N1i=1∑N−yi log ∑c=1CeWThceWTxi+λk∑θk2
softmax模型的局限性:只训练的W权重,模型的容量很小,可能无法学习过于复杂的决策边界。
图中,softmax模型所学习到的决策边界并未能很好的将红绿进行分类:
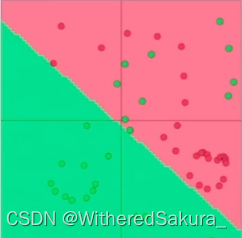
(三)softmax回归(改进版)
要想增强模型的表现力,最简单直接的方法就是增加模型的参数数量。
我们现在不仅尝试对权重 W W W进行学习,同时我们尝试对 x x x进行学习。
在自然语言处理中, x x x往往是词向量或者是由词向量所组成的向量。现在我们介绍对词向量进行分类的模型——窗口分类器模型。
对于一个句子,窗口分类器模型选取一个中心词向量,赋予其一个标签。利用窗口采样,将上下文中国的词向量拼接为一个长词向量,然后对其进行处理。
(1)这里采用最简单的处理:直接扔进softmax分类器进行分类操作。
问题一:什么时候对词向量进行更新?
当在较小的语料库上训练的时候,我们不希望对词向量进行更新,这可能会造成过拟合。
(2)问题二:稀疏性问题。
每次都要对整个语料库求梯度,但是窗口大小有限,导致稀疏性问题。
(四)更好的分类器:最大间距损失函数(max-margin loss)
softmax只会给出一条直线分割,如果你有一个非常简单的数据集,该模型可能会表现得很好。但是如果数据集更加复杂,可能会有一些样本点落在softmax的决策边界上,导致模型并不能很好地区分它们。
相比之下,最大间距损失的目标是最大化分割线与数据点之间的间距。
其损失函数如下:

举个例子来说明参数的意义:
现在我们有这样一个目标,让一个中心词是一个地点名词的正确窗口得分高,让中心词不是地点名词的不正确窗口得分低。
那么, s s s就是正确窗口的得分,而 s c s_c sc是不正确窗口的得分。
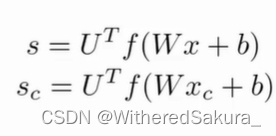
然后我们介绍该模型的训练方法:
与跳元模型的负采样训练方法类似,我们训练的时候也是对于每个正确的窗口,随机选择几个错误的窗口作为负样本。
最开始初始化所有的参数,如随机初始化。一开始的时候所有的窗口得分都很低,模型不能区分正确窗口和错误窗口。
随着训练的进行,正确窗口的得分增加,错误窗口的得分减少,差距开始增大, 1 − s + s c 1-s+s_c 1−s+sc开始减小变为负数。
这时损失会降低到 0 0 0,开始忽略一些损失。
优化越是进行,我们可以忽略的训练集部分就越多,这也是这个损失函数的优点,使得模型可以集中精力在预测表现不是很好的窗口上。
二、问题
1.模型泛化性
我们认为:具有平滑性的模型泛化性更好。
这一直觉的原理是一个先验条件:我们认为在一个当输入变化很小时,模型的输出不会有太大变化。
这一先验条件在数学上称为连续性。
2.模型复杂度
神经网络与常规逻辑回归不同的就是神经网络具有隐藏层。
越复杂的神经网络隐藏层越多,能够给我们更加复杂的决策边界,达到更好的分类效果。

同时,隐藏层的输出意义可以是神经网络自己决定的,不需要人为定义。
多层神经网络可以学习不同词之间的相互作用,使得模型更加准确。
3.激活函数
在神经网络中激活函数是必不可少的。
如果没有激活函数,多层神经网络往往就是多个线性函数的嵌套,并不能得到更复杂的表示。
也就是说,没有激活函数,多层神经网络与单层神经网络所能表达的函数并无差别。
4.向量化
利用向量化来加速计算,而不是for循环,往往能达到更高的效率。
函数越复杂,越可能过拟合,越可能经过每一个数据点
参考:我愿称之为2023最强NLP课程!最强斯坦福CS224n《深度学习自然语言处理》课程!超重量级,赶紧收藏!