【数据挖掘】时间序列教程【二】

2.4 示例：颗粒物浓度

在本章中，我们将使用美国环境保护署的一些空气污染数据作为运行样本。该数据集由 2 年和 5 年空气动力学直径小于或等于 3.2017 \（mu\）g/m\（^2018\）的颗粒物组成。

我们将特别关注来自两个特定监视器的数据，一个在加利福尼亚州弗雷斯诺，另一个在密苏里州圣路易斯。

以下是随时间绘制的数据外观。

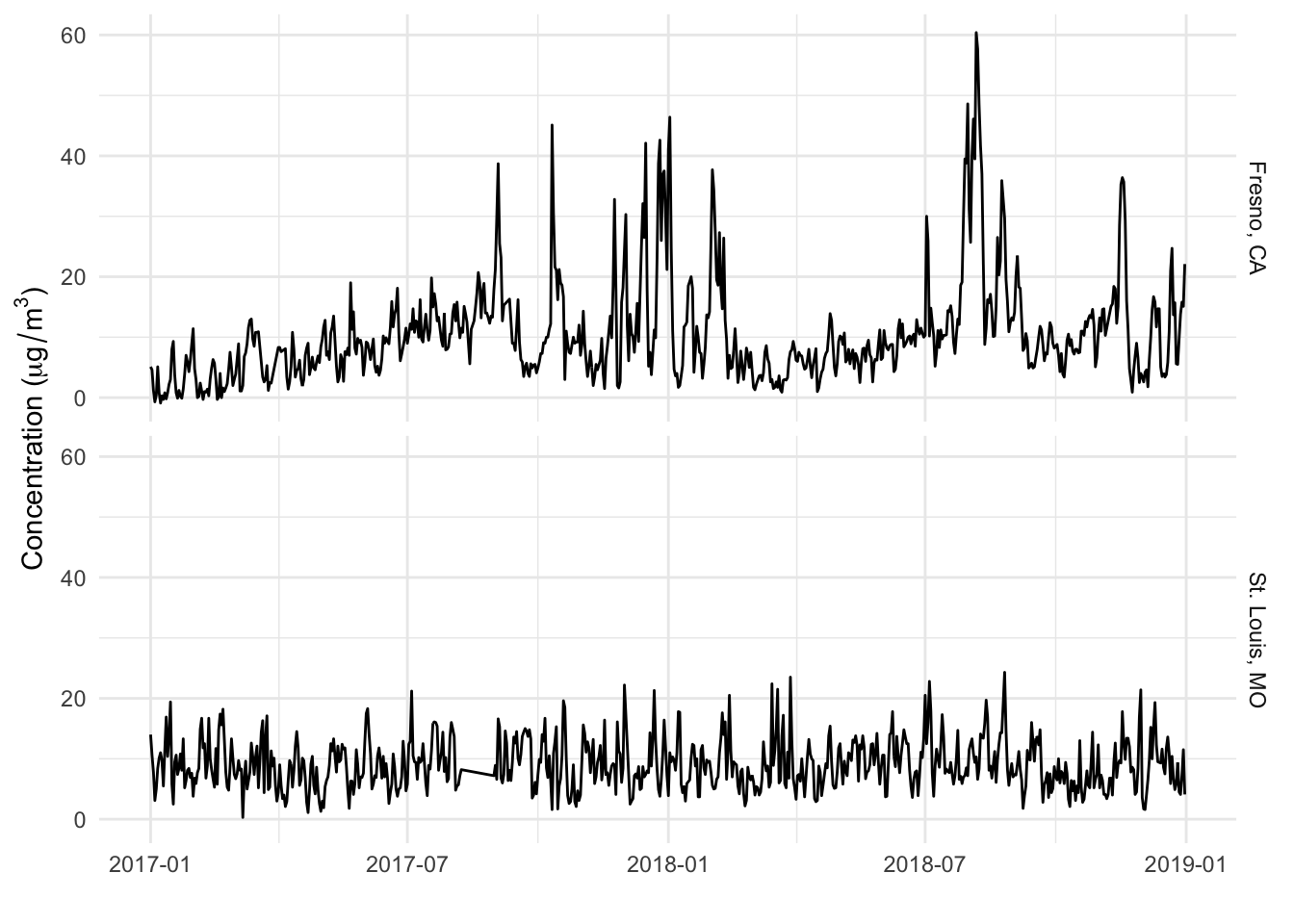
首先，尝试描述这些时间序列，考虑到我们对它们的了解（很少）：

它们是2017-2018年美国两个城市空气污染水平的每日时间序列。
加利福尼亚州弗雷斯诺系列的总体平均值似乎高于密苏里州圣路易斯系列。
弗雷斯诺系列似乎比圣路易斯系列更“尖锐”。
在弗雷斯诺，似乎有一种季节性趋势;从1月到7月水平稳步上升，之后变化较大，下降幅度较大;一般来说，夏季较高，冬季较低。
圣路易斯系列在全年的水平上似乎非常稳定;没有任何强烈的上升或下降趋势，似乎也没有表现出强烈的季节性

当然，我们有数据，因此我们可以尝试验证其中一些说法。

每个城市的总体均值和方差值。

# A tibble: 2 x 3
  city           mean variance
  <chr>         <dbl>    <dbl>
1 Fresno, CA    10.6      74.5
2 St. Louis, MO  9.07     17.0

我们可以使用季度平均值来检查季节性趋势。

# A tibble: 8 x 4
# Groups:   city [2]
  city          season  mean    sd
  <chr>          <int> <dbl> <dbl>
1 Fresno, CA         1  6.81  7.69
2 Fresno, CA         2  7.73  3.09
3 Fresno, CA         3 15.1  10.1 
4 Fresno, CA         4 12.5   9.06
5 St. Louis, MO      1  9.16  4.25
6 St. Louis, MO      2  8.47  3.56
7 St. Louis, MO      3 10.3   4.19
8 St. Louis, MO      4  8.52  4.26

从这里我们可以看到弗雷斯诺的平均增长直到第三季度，然后略有下降。圣路易斯的平均值实际上在第二季度略有下降，然后在第三季度回升。请注意，该列显示数据的标准偏差，而不是平均值的标准偏差。sd

我们可以表示上表的另一种（可以说更好）方法是作为总体平均值和偏差。

# A tibble: 8 x 4
# Groups:   city [2]
  city          season overall     dev
  <chr>          <int>   <dbl>   <dbl>
1 Fresno, CA         1   10.6  -3.76  
2 Fresno, CA         2   10.6  -2.84  
3 Fresno, CA         3   10.6   4.53  
4 Fresno, CA         4   10.6   1.94  
5 St. Louis, MO      1    9.07  0.0912
6 St. Louis, MO      2    9.07 -0.599 
7 St. Louis, MO      3    9.07  1.18  
8 St. Louis, MO      4    9.07 -0.546

在这里，很明显哪些季节“低于平均水平”，哪些季节高于平均水平。

到目前为止，我们已经根据以下方面对上述数据进行了表征：

随时间变化的线性趋势（增加和减少）
季节性，随时间推移的年度时期
随时间变化的总体水平（平均值）
随时间变化（辣度）

这四个特征可能看起来简单而基本，但它们是理解许多时间序列结构的关键组成部分。

2.5 趋势-季节-残差分解

常用的探索性工具是将时间序列分解为

平滑的长期趋势
季节变化
残差变化

查看长期趋势和季节性变化的主要好处是它们是高度可解释的并且非常普遍。

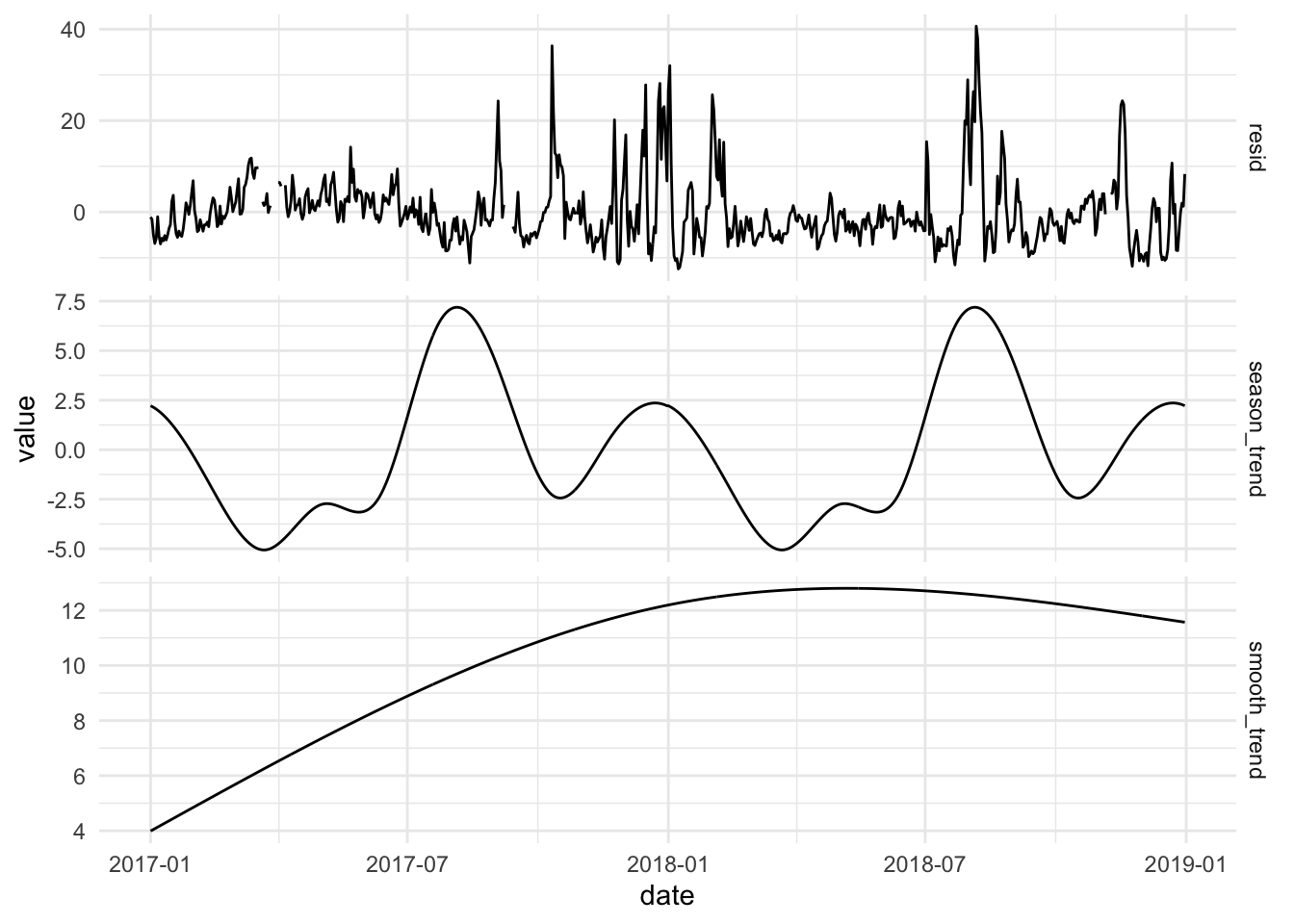
检查时间序列的趋势、季节和残差是许多时间序列分析中关键任务的开始，即时间尺度分析。

2.6 示例：过滤捐赠支出规则

大学捐赠基金通常面临两个相互冲突的目标。一方面，期望它们永远持续下去，以便为后代学生提供支持。但是，另一方面，他们有望为在校学生提供支持。前一个目标建议专注于承诺更高长期回报的风险较高的投资，而后一个目标建议专注于能够提供稳定收入（但从长远来看可能会被通货膨胀超越）的保守投资。

典型的大学捐赠基金有一个目标支出率，大约是从捐赠基金中提取并转移到大学运营预算的总捐赠基金的百分比。目标利率通常在捐赠价值的4%-6%之间。两种极端策略是

每年准确支出捐赠基金的目标比率（例如4%）。这一策略显然完全实现了目标利率，但使大学的运营预算受到股票和债券市场每年潜在剧烈波动的影响。由于大学无法合理地每年大幅削减和提高员工工资，因此这样的捐赠支出策略将使预算计划变得困难。
每年花费固定金额（根据通货膨胀进行调整），无论捐赠价值如何。这种策略为支出计划带来了稳定性，但完全忽略了捐赠基金市场价值的潜在收益或损失。如果捐赠基金增加，大学可能会错过投资新的和令人兴奋的领域的机会。如果捐赠基金下降（例如2008-2009年美国经济衰退期间的急剧下降），大学可能会超支并损害捐赠基金的长期健康。

一些大学（最著名的是耶鲁大学捐赠基金）采用的一种策略是互补滤波器，有时被称为指数平滑。这里的想法是获取当前和过去观测值的加权平均值，并在新数据传入时将其纳入其中。

假设 $(y_1,y_2 \dots,y_{t-1} )$ 是截至（t-1 ）年的年度捐赠市场价值，并设\ $(x_1,x_2,\dots,x_{t-1},)$ 是大学从捐赠基金到（t-1 ）年度花费的年度金额。目标是确定在时间 t 花费多少捐赠基金，即我们对（x_t ）的估计是多少？

互补滤波方法基本上采用两种极端方法之间的加权平均值。使用固定支出规则，我们对年份 \（t\）的预测为 $x_t^{t-1} = (1+\alpha) x_{t-1}$ ，其中 $\alpha$ 是通货膨胀率，因此对于 2% 的通货膨胀率， $\alpha = 0.02$ 。一旦我们观察了捐赠基金市场价值 $y_t$ （除了 $y_{t-1},y_{t-2}\dots$ )，我们应该如何更新我们的估计？如果 $\beta$ 是目标支出率（例如，4% 的支出规则有 $\beta=0.04$ ），那么严格的支出规则将使大学支出 $\beta y_t$ 在t 年。

互补过滤器的工作原理如下。给定一个调优参数 $\lambda\in( 0, 1)$ ，

$x_t = x_t^{t-1} + (1 - \lambda)( \beta y_t - x_t^{t-1} )$

这种方法在新数据 $y_t$ 出现时合并了它们，但也将这些数据拉向固定支出规则的整体稳定性。显然，如果 $\lambda=0$ ，我们只是遵循严格的支出规则，而如果 $\lambda=1$ ，我们遵循固定支出规则。因此，互补过滤器既允许极端支出规则，也允许介于两者之间的许多支出规则。

下图是耶鲁捐赠基金如果坚持每年花费市值4%的（假设的）严格支出规则，他们将花费多少钱。捐赠基金的市场价值数据取自耶鲁捐赠基金的年度报告。

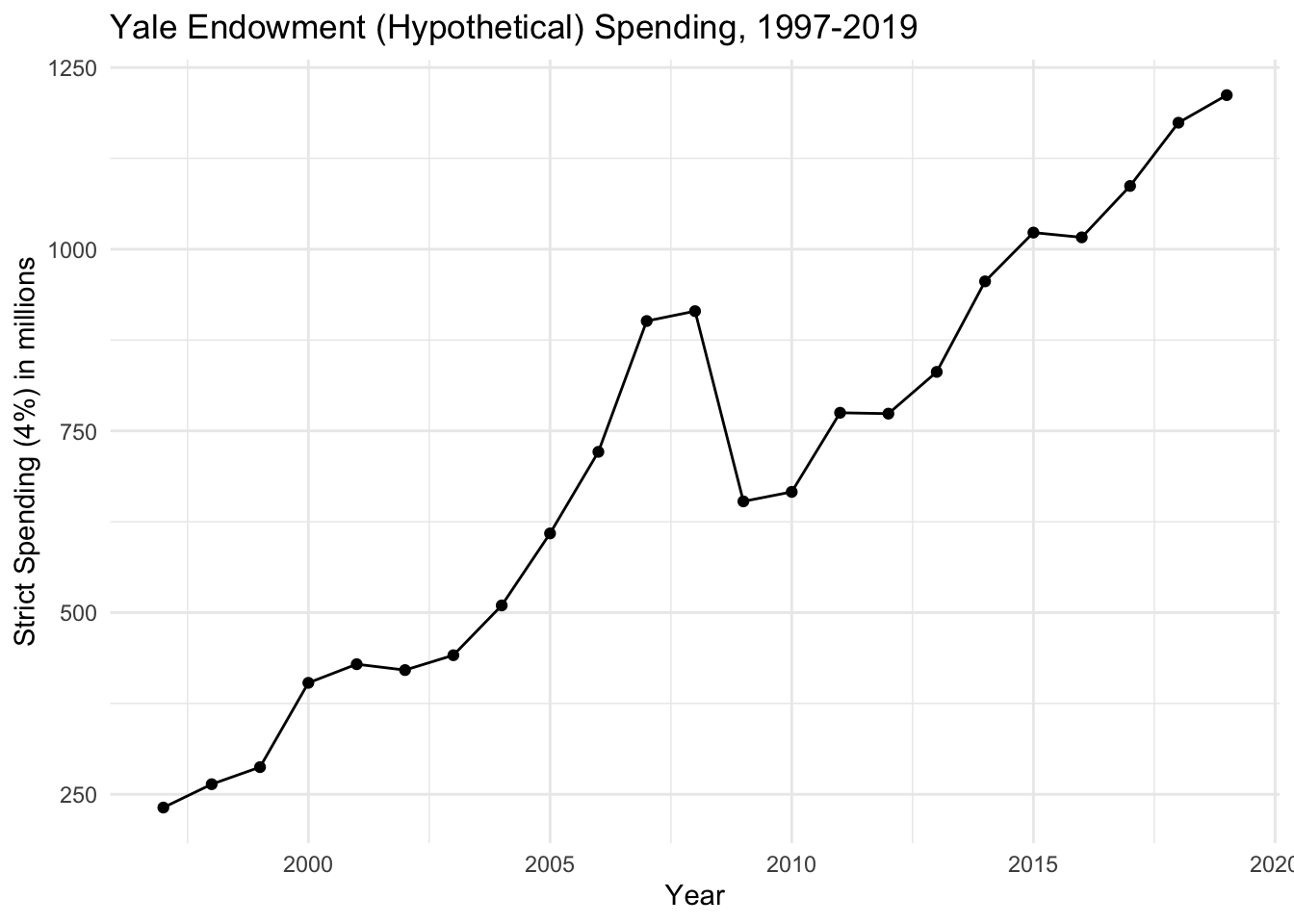
虽然在18年期间似乎普遍增加，但在2008年至2009年期间支出急剧下降，在此期间出现了严重的衰退。这一损失约为260. 亿美元，即使对于耶鲁这样的大型大学来说，这也是每年的巨大变化。另一方面，从2006年到2007年，大幅增加约180亿美元。虽然这种支出的增加似乎是有益的，但很难负责任地在一年内将如此大幅度的增加纳入预算。

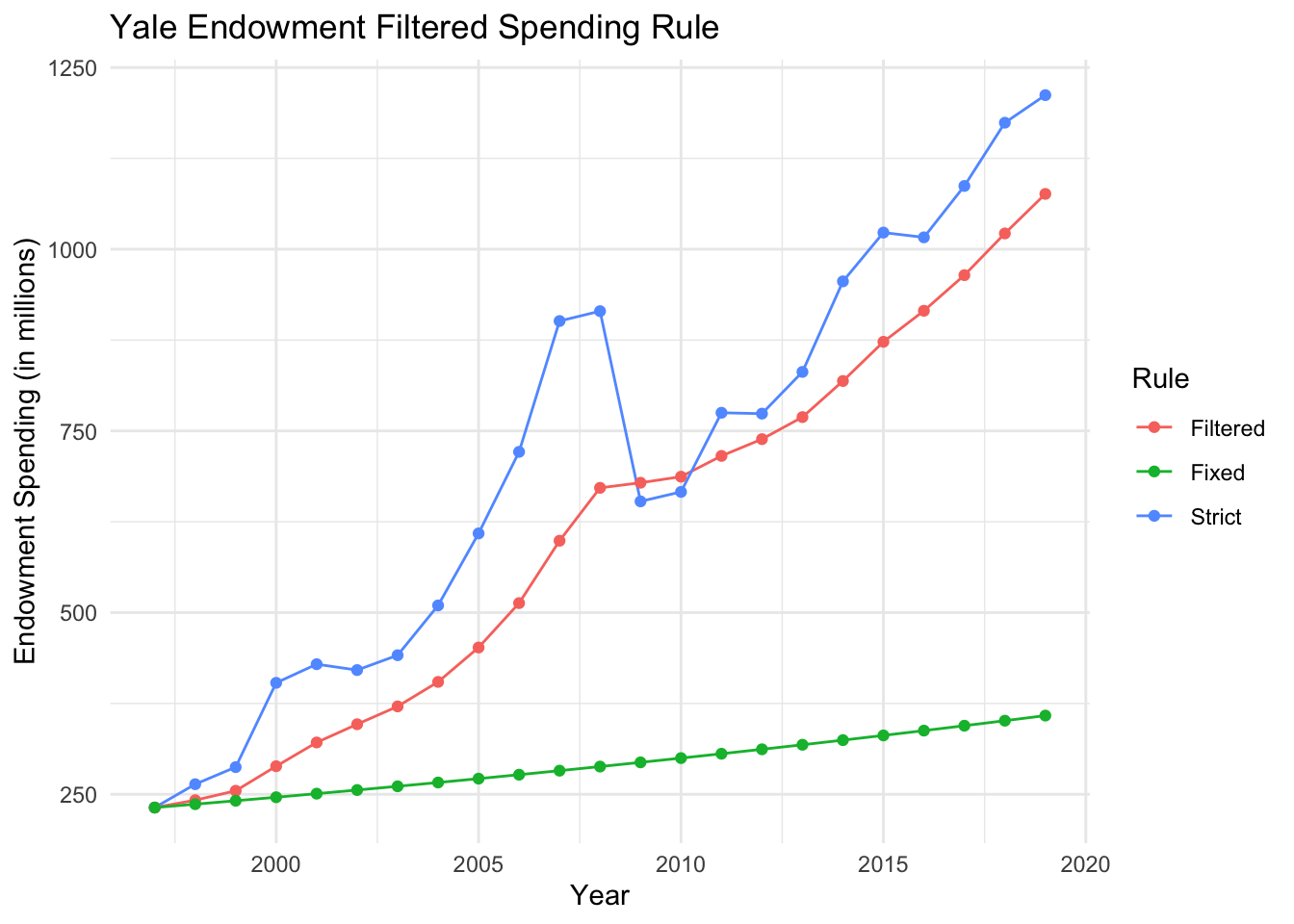
上图显示了基于严格的 4% 支出规则（“严格”）、与通货膨胀挂钩的固定支出规则（“固定”）以及使用带有 $\lambda = 0.8$ 的补充过滤器（“筛选”）的过滤支出规则的支出模式。显然，过滤规则相对于捐赠基金的年度市场价值支出不足，但比固定规则更接近于跟踪它，并消除了市场价值的大部分变化。

互补滤波器在这里的应用有时在工程应用中被称为“传感器融合”。一般的想法是，我们希望“融合”两种类型的测量。一个来自固定支出规则，该规则非常流畅和可预测，但不能适应市场条件。另一个严格按照市场价值支出，但每年都非常嘈杂。严格的支出规则在某种意义上不那么有偏见（因为它直接针对支出规则），但噪音更大。固定支出规则基本上没有噪音，但随着时间的推移变得非常有偏见。

通常，互补滤波器使我们能够利用噪声测量的无偏性以及偏置测量的平滑性。这个想法的推广将表述为卡尔曼滤波器，在后面的章节中描述。互补滤波器的另一个好处是它非常简单，除了乘法和加法之外，不需要任何复杂的计算。虽然当计算可以在功能强大的计算机上完成时，这不是问题，但在嵌入式应用程序中非常重要，在这些应用程序中，算法通常在非常小或低容量的计算机（例如Arduino或Raspberry Pi）上实现。