摘要
剑指 Offer 40. 最小的k个数
一、排序方法
1.1 排序的方法分析
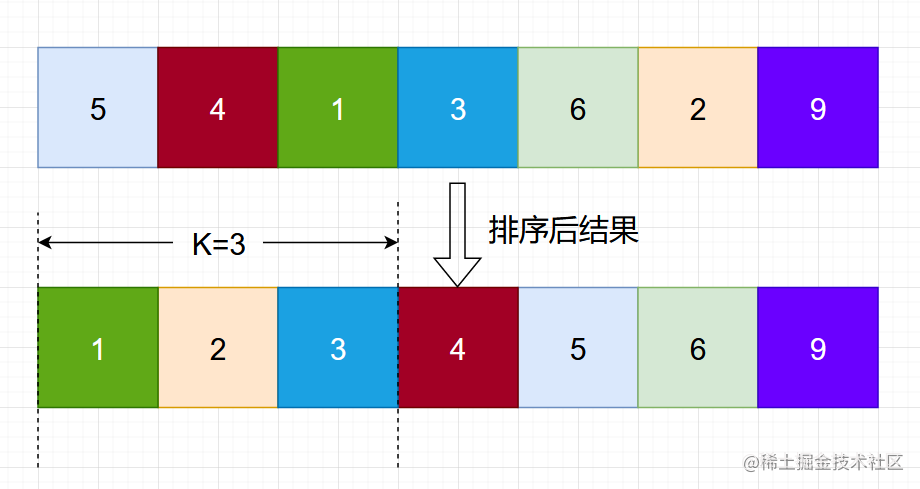
对原数组从小到大排序后取出前 k 个数即可。
1.2 复杂度分析
-
时间复杂度:O(nlogn)O,其中 n 是数组 arr 的长度。算法的时间复杂度即排序的时间复杂度。
-
空间复杂度:O(logn),排序所需额外的空间复杂度为 O(logn)。
1.3 code 示例
public int[] getLeastNumbers(int[] arr, int k) {
Arrays.sort(arr);
int[] result=new int[k];
int index=0;
while (index<k){
result[index]=arr[index];
index++;
}
return result;
}
二、大顶堆和小顶堆
2.1 大顶堆和小顶堆的思路分析
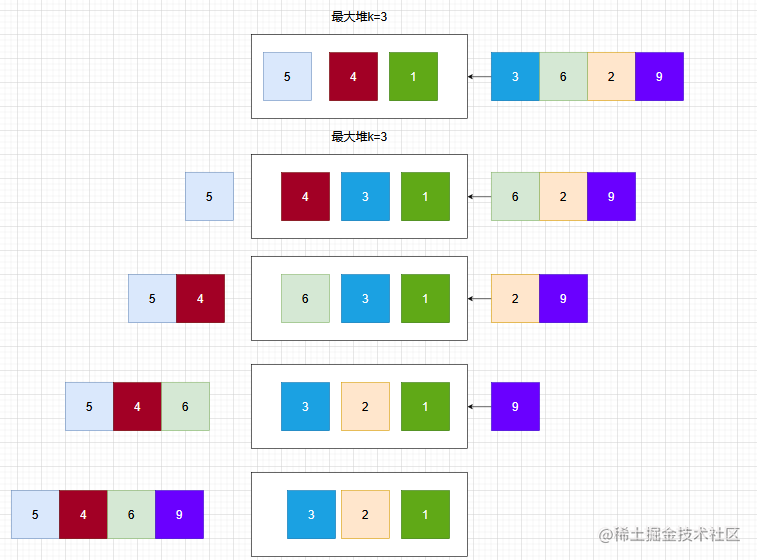
堆的性质是每次可以找出最大或最小的元素,我们用一个大根堆实时维护数组的前 k 小值。首先将前 k个数插入大根堆中,随后从第 k+1个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。
2.2 复杂度分析
-
时间复杂度:O(nlogk),其中n是数组 arr 的长度。由于大根堆实时维护前 k 小值,所以插入删除都是 O(logk) 的时间复杂度,最坏情况下数组里 n 个数都会插入,所以一共需要 O(nlogk) 的时间复杂度。
-
空间复杂度:O(k),因为大根堆里最多k个数。
2.3 code 示例
/**
* @description 利用小顶堆的数据结构来实现数据找到最小的那几个数据
* @param: arr
* @param: k
* @date: 2022/12/7 11:06
* @return: int[]
* @author: xjl
*/
public int[] getLeastNumbers2(int[] arr, int k) {
int[] vec=new int[k];
if (k==0){
return vec;
}
// 构建的是一个的优先队列 小根堆数据结构
PriorityQueue<Integer> queue=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
// 添加k个值到小根堆中
for (int i=0;i<k;i++){
queue.offer(arr[i]);
}
for (int i=k;i<arr.length;i++){
if (queue.peek()>arr[i]){
queue.poll();
queue.offer(arr[i]);
}
}
for (int i=0;i<k;i++){
vec[i]=queue.poll();
}
return vec;
}
三、快排思想
3.1 快排思想分析
实际上这个就是的排序的思想。
题目只要求返回最小的k个数,对这k个数的顺序并没有要求。因此,只需要将数组划分为最小的k个数和其他数字两部分即可,而快速排序的哨兵划分可完成此目标。
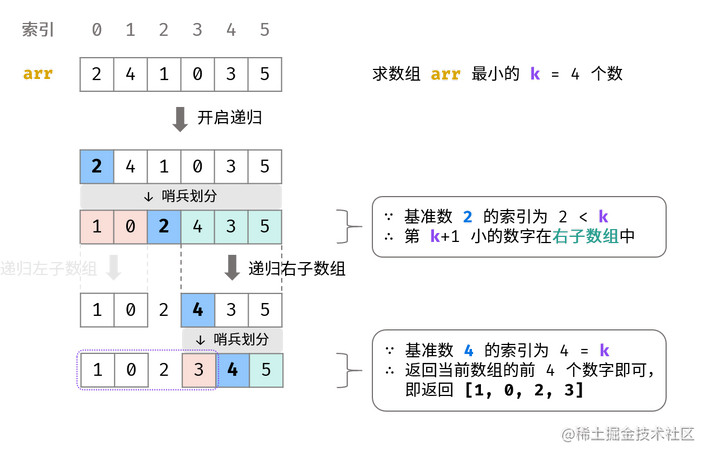
根据快速排序原理,如果某次哨兵划分后基准数正好是第k+1小的数字,那么此时基准数左边的所有数字便是题目所求的最小的k个数。
根据此思路,考虑在每次哨兵划分后,判断基准数在数组中的索引是否等于k ,若true则直接返回此时数组的前k个数字即可。
算法流程:
- getLeastNumbers() 函数:
- 若 kk 大于数组长度,则直接返回整个数组;
- 执行并返回
quick_sort()即可;
- quick_sort() 函数:
注意,此时
quick_sort()的功能不是排序整个数组,而是搜索并返回最小的 k个数。
-
哨兵划分:
- 划分完毕后,基准数为
arr[i],左/右子数组区间分别为 [l,i−1] , [i+1,r];
- 划分完毕后,基准数为
-
递归或返回
- 若 k<i ,代表第 k+1 小的数字在 左子数组 中,则递归左子数组;
- 若 k>i ,代表第 k+1小的数字在 右子数组 中,则递归右子数组;
- 若 k=i ,代表此时 arr[k] 即为第 k+1小的数字,则直接返回数组前 k 个数字即可;
3.2 复杂度分析
-
时间复杂度 O(N) : 其中 N 为数组元素数量;对于长度为 N 的数组执行哨兵划分操作的时间复杂度为 O(N)。
-
空间复杂度 O(logN) :划分函数的平均递归深度为 O(logN) 。
3.3 code 示例
/**
* @description 手动实现快排的思想来完成
* @param: arr
* @param: k
* @date: 2022/12/7 11:30
* @return: int[]
* @author: xjl
*/
public int[] getLeastNumbers4(int[] arr, int k) {
if (k >= arr.length) {
return arr;
}
return quickSort(arr, k, 0, arr.length - 1);
}
private int[] quickSort(int[] arr, int k, int l, int r) {
int i = l, j = r;
while (i < j) {
// j 向左边里面走
while (i < j && arr[j] >= arr[l]) {
j--;
}
// i向右边走
while (i < j && arr[i] <= arr[l]) {
i++;
}
swap(arr, i, j);
}
// 交换的是的i 和左边选定的基准值
swap(arr, i, l);
if (i > k) {
return quickSort(arr, k, l, i - 1);
}
if (i < k) {
return quickSort(arr, k, i + 1, r);
}
// 如果是的i=k 那就表前k个数据是有序的。
return Arrays.copyOf(arr, k);
}
private void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}