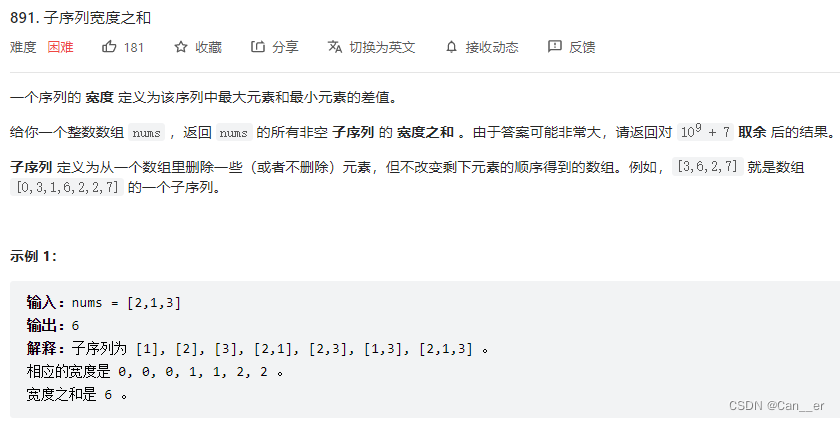
891. 子序列宽度之和

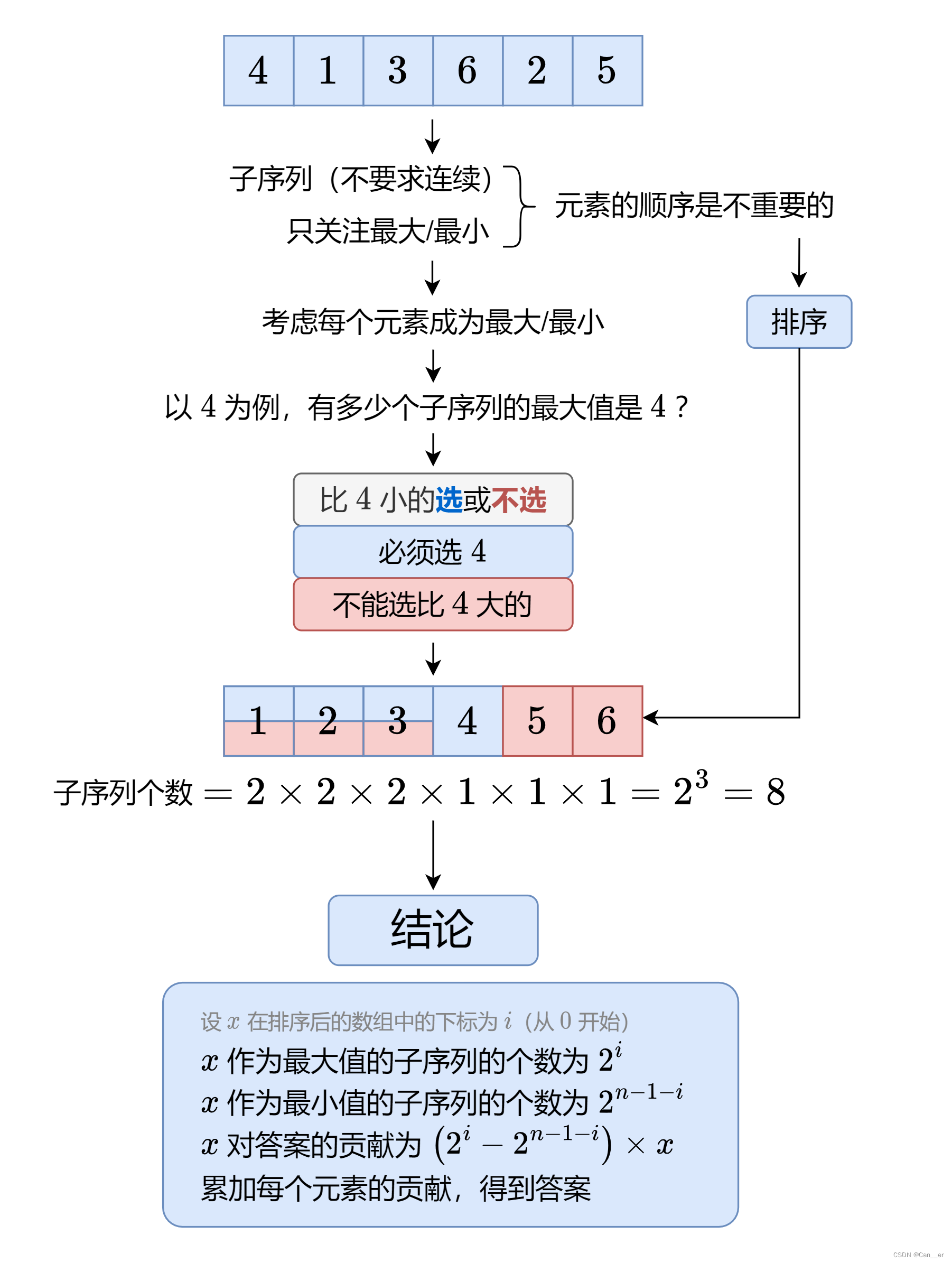
计算的是【贡献】。
首先观察发现，顺序不影响结果。然后比如1，作为最大元素贡献为0，而作为最小元素贡献为每个子序列的【最大-1】，一共有多少个作为最小元素的子序列，对答案的贡献就是-1*(个数)。
考虑子序列个数，比他小的不能选，那么比他大的n-1个可选可不选，是2的n-1次方个。
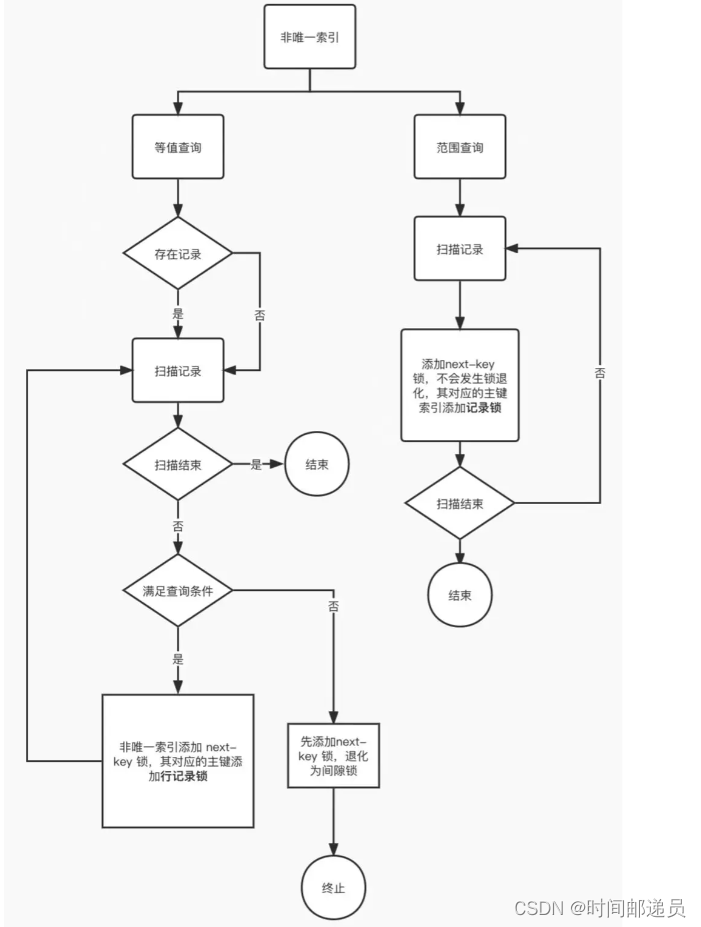
这里放一个0x3f的解法图：

792. 匹配子序列的单词数

这个题使用多指针的想法是很自然的，遍历s的同时更新每个word的指针。但难点在于复杂度，1 <= s.length <= 5 * 104 的长度，使得遍历s更新words的操作是不可取的。
所以想到了根据word中的字符去匹配s中的字符，对每一个c而言，不再检查所有的word，而是直接通过字典获取这是第几个word的第几个字母，直到匹配到和word长度一样，则ans+=1。

class Solution:
    def numMatchingSubseq(self, s: str, words: List[str]) -> int:
        p = defaultdict(list)
        for i, w in enumerate(words):
            p[w[0]].append((i, 0))
        ans = 0
        for c in s:
            q = p[c]
            p[c] = []
            for i, j in q:
                j += 1
                if j == len(words[i]):
                    ans += 1
                else:
                    p[words[i][j]].append((i, j))
        return ans

813. 最大平均值和的分组

首先一条是：分的组越多，得到的结果越大。
使用dp[i][j]表示区间[0, i-1]切分成j个子数组。

第一条很好理解，就是求一整个大组的平均值。这里可以使用前缀和的方式求。
第二条则引入x，x是划分的下标。因为j个组相比j-1个组而言，不一定是哪里划分的，所以需要枚举x的位置。
而因为是把前i个字母切分成j个，所以需要x>=j-1。

class Solution:
    def largestSumOfAverages(self, nums: List[int], k: int) -> float:
        n = len(nums)
        prefix = list(accumulate(nums, initial=0))
        dp = [[0.0] * (k + 1) for _ in range(n + 1)]
        for i in range(1, n + 1):
            dp[i][1] = prefix[i] / i
        for j in range(2, k + 1):
            for i in range(j, n + 1):
                for x in range(j - 1, i):
                    dp[i][j] = max(dp[i][j], dp[x][j - 1] + (prefix[i] - prefix[x]) / (i - x))
        return dp[n][k]