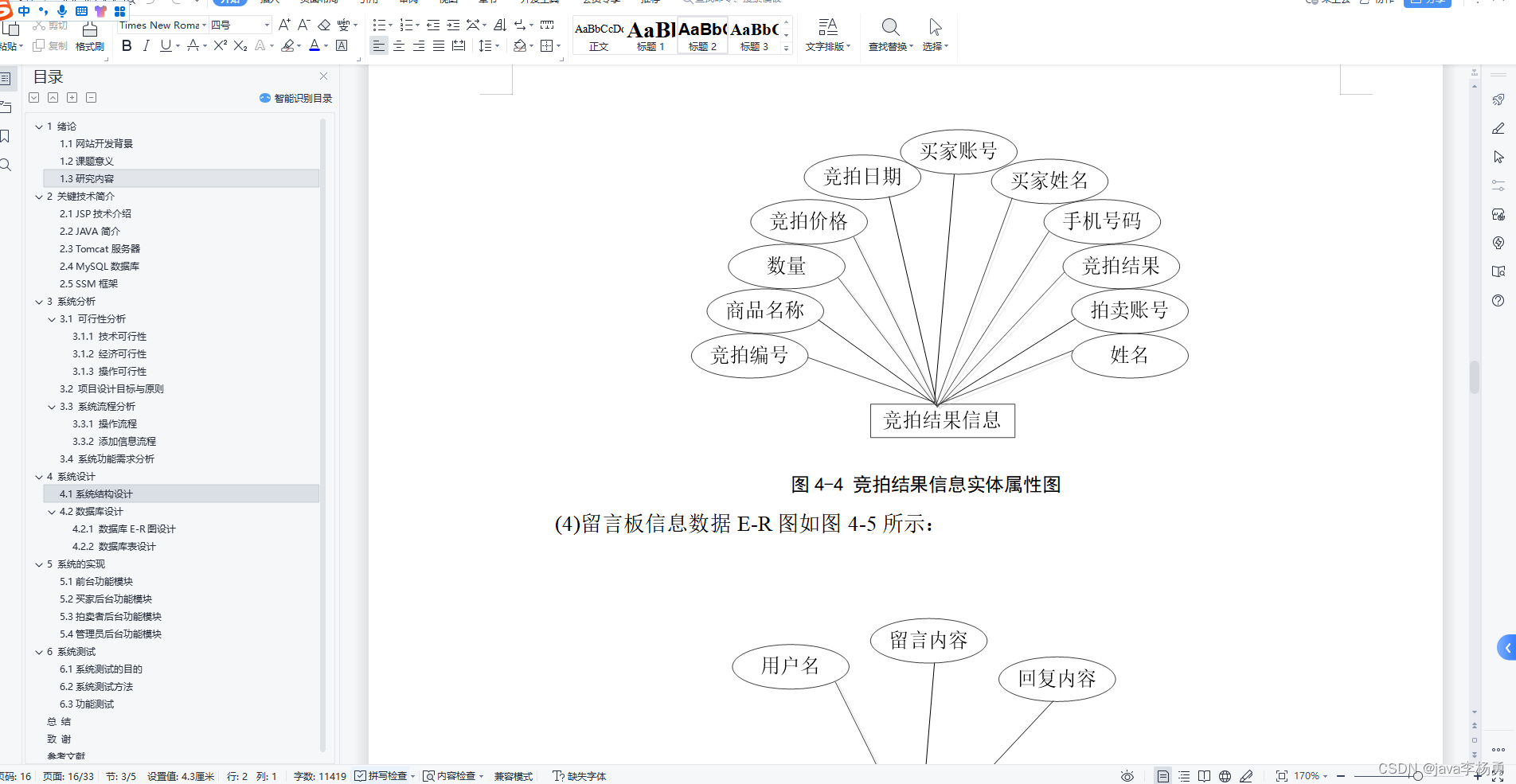
论文链接:https://arxiv.org/abs/2102.09844
- 一种新模型来学习与旋转、平移、反射和排列等变的图神经网络,称为 E(n)-等变图神经网络 (EGNN)
尽管深度学习在很大程度上取代了手工制作的特征,但许多进步严重依赖于深度神经网络中的归纳偏差。(inductive bias)
将神经网络限制为和研究问题相关函数的一种有效方法是,利用问题的对称性、变换等变性(equivariance),通过研究某个对称组来简化当前问题的计算。
- CNN的卷积是等变形、池化是近似不变性;
- GNN的点的排列顺序是等变性(不同点的排列对应不同的邻接矩阵,但是最终这张graph表达的信息是一样的)
许多问题都表现出 3D 平移和旋转对称性
- 这些对称操作的集合记为SE(3) ,如果包含反射,那么集合记为 E(3)。 通常希望对这些任务的预测相对于 E(3) 变换是等变的或不变的。
最近,已经提出了等变E(3) 或 SE(3) 的各种形式和方法。 其中许多工作在研究中间网络层的高阶表示类型方面实现了创新。 然而,这些高阶表示的转换需要计算成本高昂的系数或近似值。 此外,在实践中,对于许多类型的数据,输入和输出仅限于标量值(例如温度或能量,在文献中称为 type-0)和 3D矢量(例如速度或动量,在文献中称为 type-1)
它是平移、旋转和反射等变 (E(n)),以及关于输入点集的置换等变。 模型比以前的方法更简单,同时模型中的等变性不限于 3 维空间,并且可以扩展到更大的维空间,而不会显着增加计算量。

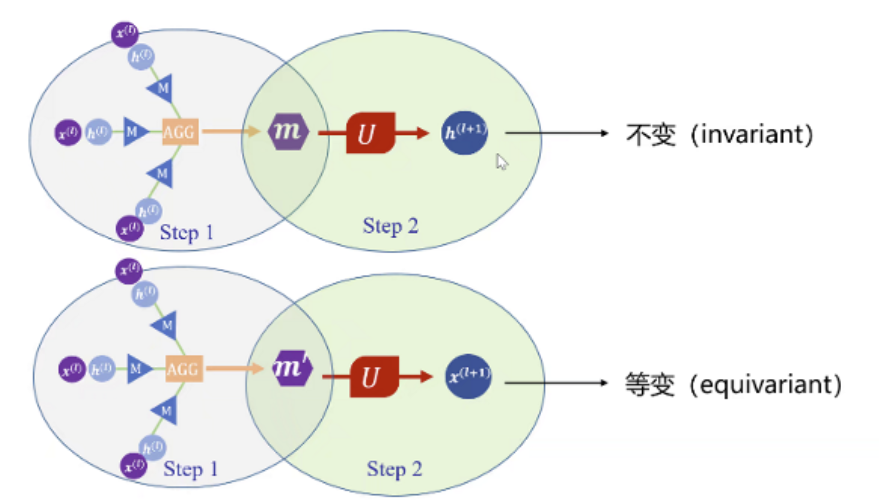
等变性:先平移/旋转/排列再映射,和先映射再平移/旋转/排列 效果是一样的
论文中探索了三种等变性:
- Translation equivariance
- Rotation and relection equivariance
- Permutation equivariance.
- 置换同变性:
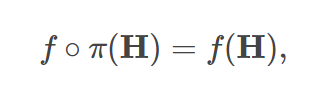
- 置换不变性:
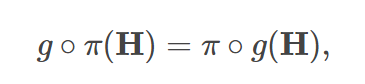
- 简单来说,置换不变性使得输出与输入顺序无关,而置换同变性使得输出顺序与输入顺序对应。
- 显然置换同变函数后面接一个置换不变的函数,得到的函数还是置换不变的。
- 什么时候需要这两类函数?因为图天然具有无序性,当我们关心节点特征时,我们希望改变节点标号时,节点特征不变,或者说节点特征的排序要根据节点编号做出重排,这时候就需要置换同变性;当我们关心图特征时,希望改变节点标号不影响图特征,就需要置换不变性。
- GNN 的置换同变性称为全局同变性(Global Equivariance),将聚合算子的置换不变性称为局部不变性(Local Invariance),显然,
局部不变性诱导全局同变性。- 聚合算子的置换不变性对于全局的置换同变性来说,是非必要的
- 直接定义全部同变 GNN 仅有理论价值,无实际价值
- 那么有没有办法设计新的不满足不变性的聚合算子,使得 GNN 整体上仍具有同变性,但是具有更强的表达能力呢?答案是肯定的,只需引入局部同变性(Local Equivariance),即
局部同变性:相同邻域结构的节点具有相同的表示

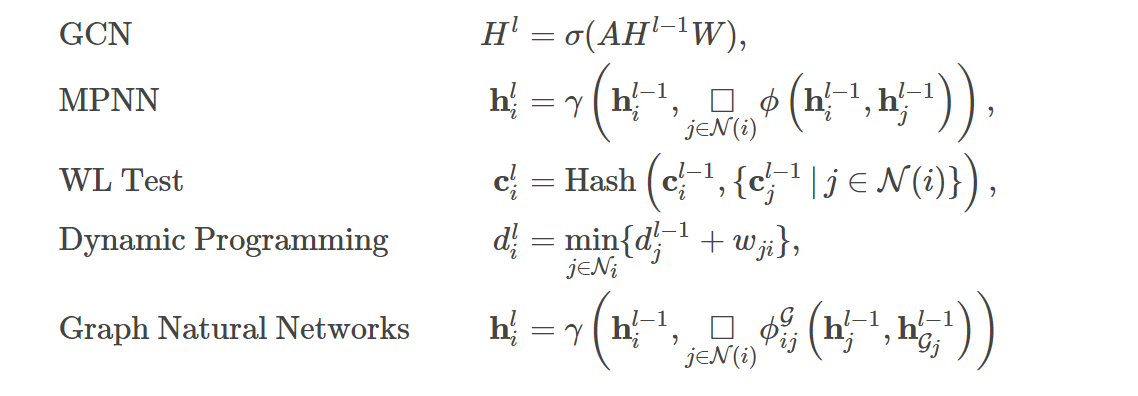
- 置换同变性:
- 三大关键点:消息函数、更新函数和聚合函数 , 这决定了GNN的表达能力
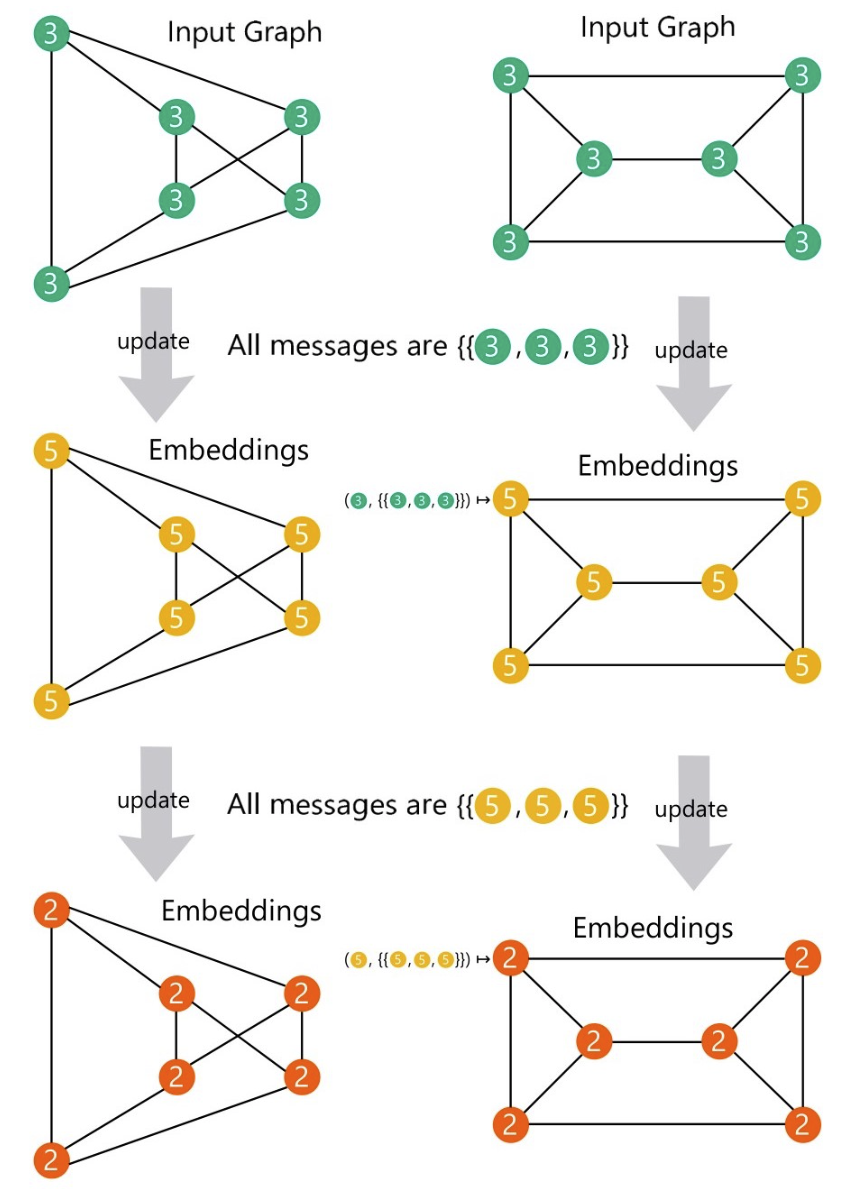
参考:https://www.cnblogs.com/hilbert9221/p/14443747.html
消息传递框架 MPNN


GCN & GAT & GSAGE
https://zhuanlan.zhihu.com/p/412296850
等变神经网络综述
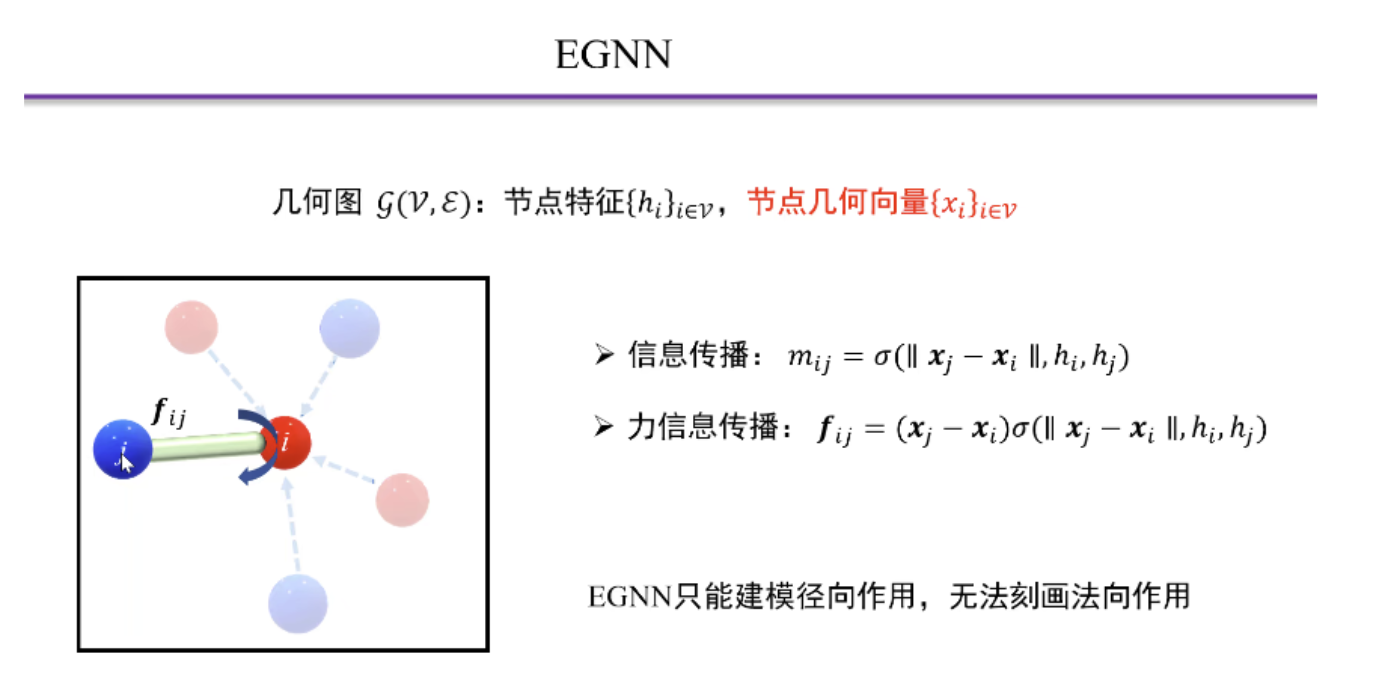
- 在物理和化学领域,很多问题需要去处理带有几何特征的图。
例如,化学小分子和蛋白质都可以建模成一个有原子和其化学键关系组成的几何图。在这个图中,除了包含原子的一些内在特征以外,我们还需要考虑到每个原子在空间的三维坐标这一几何特征。而在物理学的多体问题中,每个粒子的几何特征则包括坐标,速度,旋转等。
不同于一般特征,这些几何特征往往都具备着一些对称性和等变性。正因为如此,基于对对称性的建模,大量基于图神经网络的改进模型在近年来被提出。这一类模型,因为克服了传统图神经网络无法很好处理这类具有等变对称性质的特征的缺点,被统称为等变图神经网络。
例如,在预测分子的能量时,我们需要这个预测对于输入的几何特征是不变的,而在分子动力学应用中,我们则需要预测的结果和输入的几何特征是等变的。
通用框架
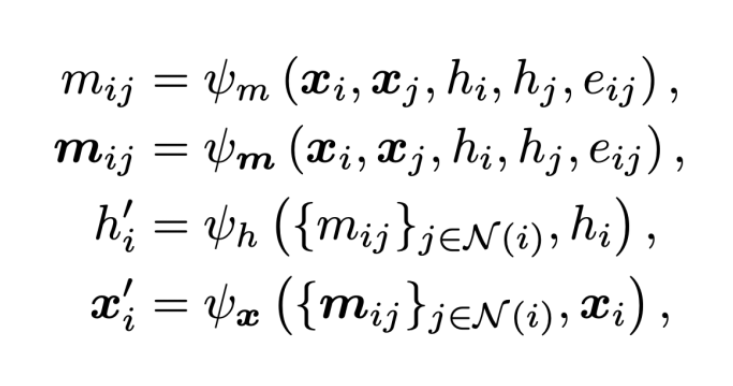
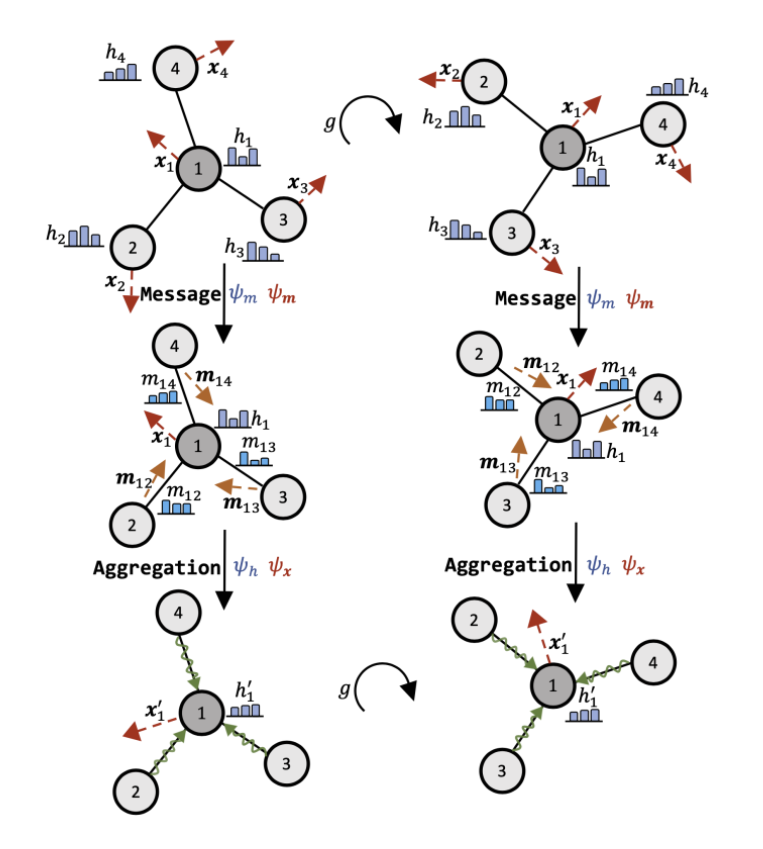
基于不可约表示信息的模型
这类模型基于表示论中关于紧群的线性表示可以拆解为一系列的不可约表示的直积这一理论。从而在 SE(3) 群中构建满足等变性质的消息模型。
- 例如,在 TFN 中:

有大量的工作基于 TFN 结构做了相应的扩展,例如加入 Attention 机制, 引入非线性的 Clebsch-Gordan 系数等。但是这类方法计算复杂度都较高,且不可约表示仅仅适用于特定的群。这约束了这类模型的表达能力。
基于正则表示信息的模型

LieTransformer 基于此思想,引入了自注意力机制来进一步提高模型的性能。基于李群正则表示的模型在群的选取上更加灵活,但是由于要进行离散化和采样,需要在效率和性能之间做出权衡。同时,以上的更新只考虑了标量信息 h,但难以直接推广到对几何信息 x 的更新,除非综合哈密顿网络等工作中的更新方法。