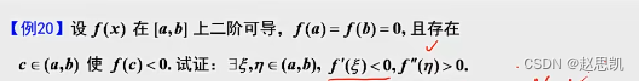目录

求函数的极值以及曲线的凹项和拐点

例题1

例题2： 

 例题3：

例题4：

 例题5：

 例题6：

求渐近线：

例题7

例题8 

例题9 

 例题10：

 方程的根

例题11：

 零点定理：

罗尔定理：

​编辑

 方程的根题目思路：

 例题12：

例题13 

 不等式的证明

 例题15：

 例题16：

 中值定理证明题：

---

求函数的极值以及曲线的凹项和拐点

例题1

 

例题2： 

 

 

 解法2：

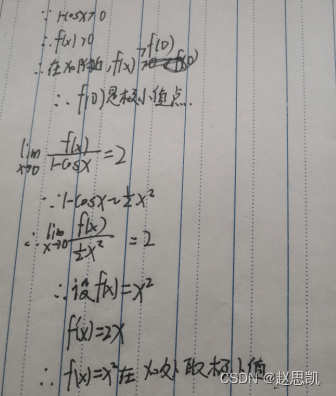
 例题3：

 

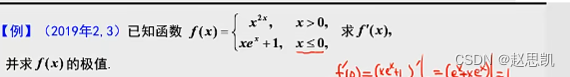
例题4：

 

 例题5：

 

 例题6：

 

求渐近线：

例题7

 我们在这里有一个结论：

当一条曲线可以写成一条直线加上一个无穷小，那么这一条直线就是这条曲线的斜渐近线。

所以对于这道题目，我们直接发现c选项有斜渐近线。

例题8 

 

例题9 

 

 

 例题10：

 

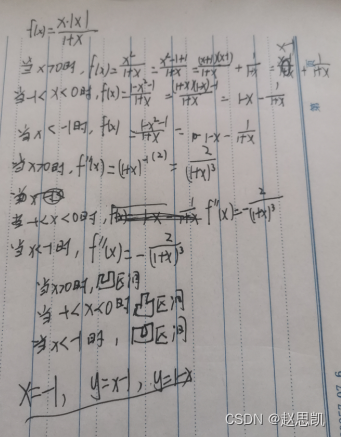
 方程的根

例题11：

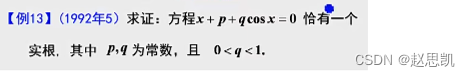
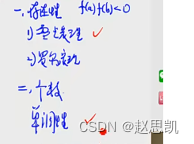
 零点定理：

 fx在区间内连续，并且在区间的两个端点是异号的，那么函数在这个区间内至少存在一个零点，也就是至少存在一个跟。

罗尔定理：

简记：闭区间连续，开区间可导，两端点值相等，存在一个点，使这个点的导数等于0. 

 方程的根题目思路：

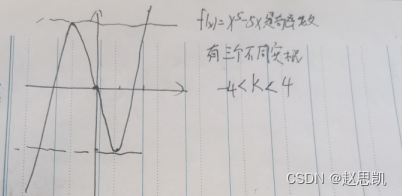
 例题12：

 

例题13 

 

 

 不等式的证明

例题14： 

 

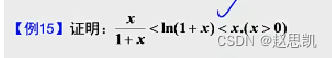
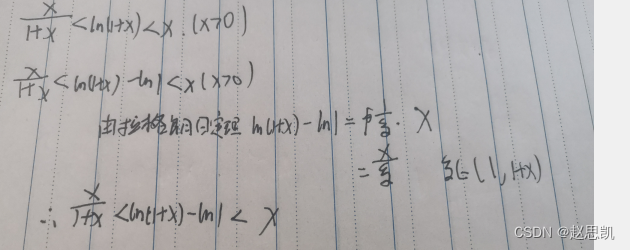
 例题15：

 

 例题16：

 

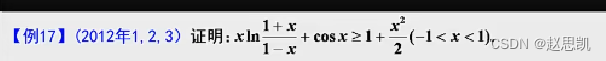
 中值定理证明题：