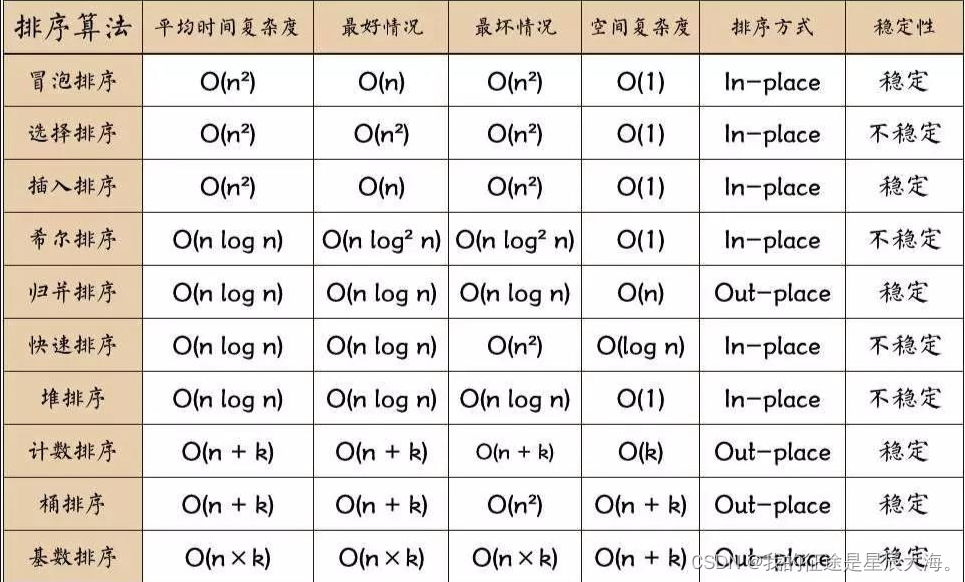
排序
1.选择排序
从待排序的数据中选择最小的元素,将其放在已排序的序列末尾,然后在剩余的数据中再选择最小的元素,放在已排序序列的末尾,以此类推,直到所有的数据都排好序为止。

public static void main(String[] args) {
int[] arr = {2,5,1,8,9};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
selectSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
/**
* 选择排序,选择最小的一个数据到第一位,第二位,等等
* @param arr 要排序的数组
*/
public static void selectSort(int[] arr){
//排除一些无用的数
if(arr == null||arr.length < 2){
return;
}
for (int i = 0; i < arr.length - 1; i++) {//1 ~ N-1,
int minIndex = i;//最小的坐标,依次更新这个最小的坐标。
for (int j = i+1; j < arr.length; j++){//从i+1的数据开始进行比较
//如果当前的数字大小小于最小值,就把当前的坐标赋值给minIndex
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
//将i位置的数字进行交换,交换成最小的值
swap(arr,i,minIndex);
}
}
/**
* 交换数组arr中i和j位置的数。
* @param arr
* @param i
* @param j
*/
public static void swap(int[] arr,int i,int j){
if(i==j) return;//排除不需要交换的数据
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
上面代码的过程
2 5 1 9 8
排序过程
按照数组的顺序,每次确定一个位置(外部循环),
依次遍历未确定的内容,找到最小(大)的,放到要排序的位置。
1 5 2 9 8 第一个位置排好
1 2 5 9 8 前两个位置排好
1 2 5 8 9 前三个位置排好
1 2 5 8 9 前四个位置排好
时间复杂度O(N^2)
额外复杂度O(1)
2.冒泡排序
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行,直到没有相邻元素需要交换,也就是说该元素列已经排序完成。

//冒泡排序
public static void main(String[] args) {
int[] arr = {2,5,1,8,9};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
bubbleSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
/**
* 相邻两个数字进行交换,一次轮询确定一个位置
* @param arr
*/
public static void bubbleSort(int[] arr){
//排除一些无用的数
if(arr == null||arr.length < 2){
return;
}
//最后一个不用排,外循环,需要确定多少个数字的位置
for (int e = arr.length - 1; e>0 ; e--) {//外层循环,在哪一轮上玩这个东西
for (int i = 0; i < e; i++) {//具体玩某一轮,某一轮的最后就是冒出的那个气泡。
if(arr[i] > arr[i+1]){
swag(arr,i,i+1);
}
}
}
}
//交换
public static void swag(int[] arr,int i,int j){
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
排序过程
依次冒出一个最大(小)的数到指定的位置
2 5 1 9 8
排序过程
第一次外循环
2 5 1 9 8
2 1 5 9 8
2 1 5 9 8
2 1 5 8 9 第一轮内循环结束,最后一个位置被确定,是9
第二次外循环
1 2 5 8 9
第三次外循环
1 2 5 8 9
第四次外循环
1 2 5 8 9
3.插入排序
将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。(就好比整理牌的时候。)

过程简单描述:
1、从数组第2个元素开始抽取元素。
2、把它与左边第一个元素比较,如果左边第一个元素比它大,则继续与左边第二个元素比较下去,直到遇到不比它大的元素,然后插到这个元素的右边。
3、继续选取第3,4,….n个元素,重复步骤 2 ,选择适当的位置插入。
public static void main(String[] args) {
int[] arr = {2,5,1,8,9};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
insertionSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
public static void insertionSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
//0-1上有序
//0-N上有序
for (int i = 1; i < arr.length; i++) {
for (int j = i-1; j >= 0 && arr[j]>arr[j+1] ; j--) { //两个体条件,在0之前,左边的数比右边的数大
swap(arr,j,j+1);
}
}
}
public static void swap(int[] arr,int i,int j){
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
过程:
2 5 1 9 8
排序过程
2 5 1 9 8 第一次循环排号了25这两个数
2 1 5 9 8 第二次循环,第一次内循环,1和5换了位置
1 2 5 9 8 第二次循环,第二次内循环,1和2换了位置
1 2 5 9 8 第三次循环
1 2 5 8 9 第四次循环
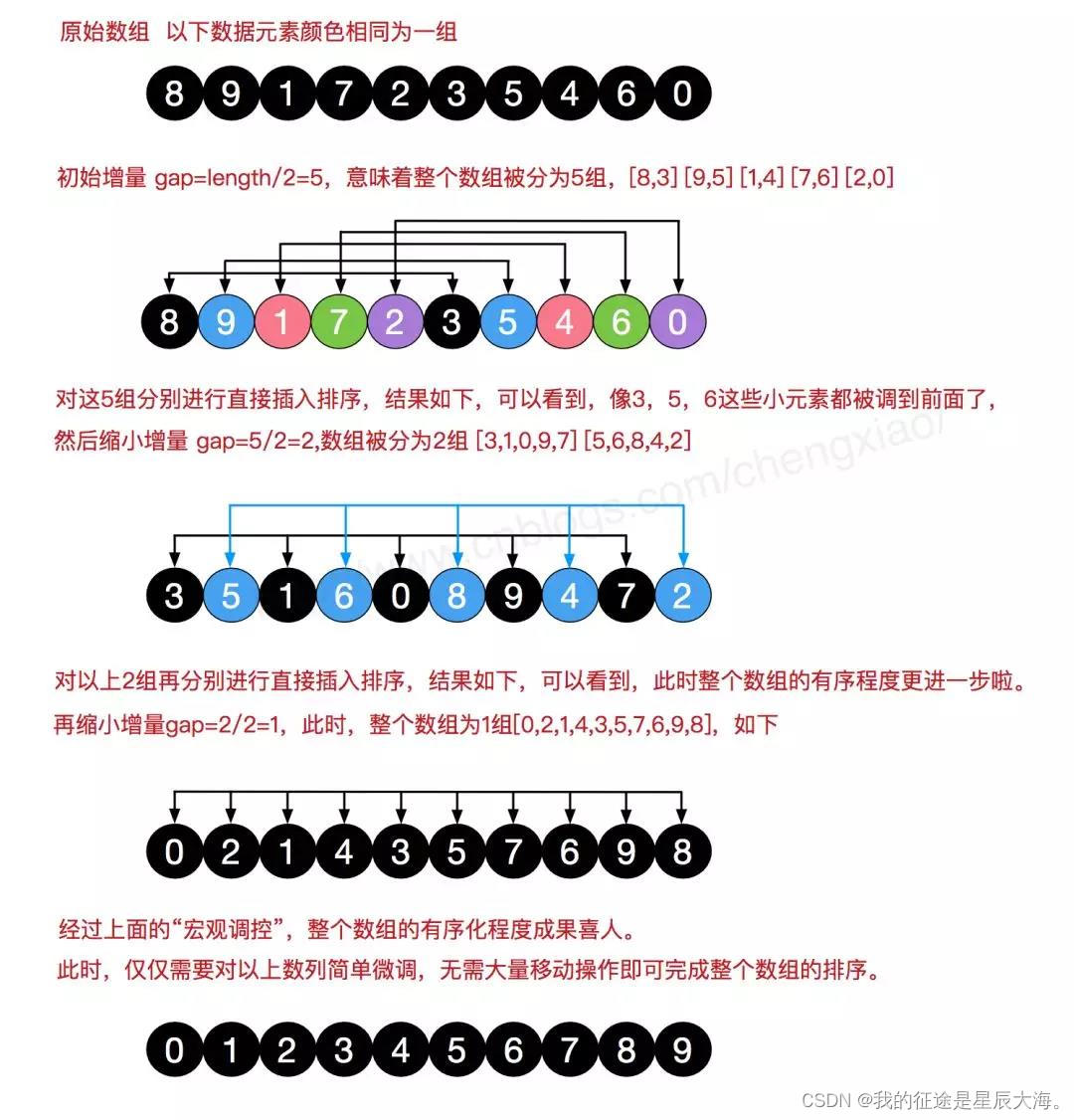
3.1 希尔排序(插入排序的一种变种)
希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。
希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
希尔排序的思想是采用插入排序的方法,先让数组中任意间隔为 h 的元素有序,刚开始 h 的大小可以是 h = n / 2,接着让 h = n / 4,让 h 一直缩小,当 h = 1 时,也就是此时数组中任意间隔为1的元素有序,此时的数组就是有序的了。
public static void main(String[] args) {
int[] arr = {1,3,4,321,2,6,254,42352,234562,4246,2,454,345};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
shellSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
/**
* 希尔排序
* @param arr
*/
public static void shellSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
//gap就是分的组数,分组越来越小
for (int gap = arr.length/2; gap > 0; gap--) {
for (int j = 0; j < arr.length - gap; j++) {
if(arr[j]>arr[j+gap]){
swap(arr,j,j+gap);
}
}
}
}
/**
* 交换数组i位置和j位置的值
* @param arr
* @param i
* @param j
*/
public static void swap(int[] arr,int i,int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
4.归并排序
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
左右分别排序,然后再将左右内容整合到一起。

public static void main(String[] args) {
int[] arr = {1,4,7,8,3,6,9};
mergeSort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
public static void mergeSort(int[] arr){
if(arr==null || arr.length<2) return;
process(arr,0,arr.length-1);
}
/**
* @param arr:要排序的数组
* @param L:数组开始的下标
* @param R:数组结束的下标
*/
public static void process(int[] arr,int L,int R){
if(L==R) return;
int mid = L + ((R-L)>>1);//获取中点位置。
process(arr,L,mid);
process(arr,mid+1,R);
merge(arr,L,mid,R);
}
/**
* @param arr:数组
* @param L:数组开始的下标
* @param M:数组的中间下标
* @param R:数组的最后的下标
*/
public static void merge(int[] arr,int L,int M,int R){
int[] help = new int[R-L+1];
int i = 0;
int p1 = L;
int p2 = M+1;
while(p1 <= M && p2 <=R){ //正常复制
//help[i++]等价于help[i] i++
help[i++] = arr[p1] <= arr[p2] ? arr[p1++]:arr[p2++];
}
while(p1<=M){//将左半部分的内容复制下来,跟下面的while循环只能有一个执行
help[i++] = arr[p1++];
}
while(p2<=R) {//将有半部分的内容复制下来
help[i++] = arr[p2++];
}
for(i=0;i<help.length;i++){
arr[L+i] = help[i];
}
}
归并排序使用的是递归方法。
1 3 4 2 5
第一次所有的都排序,分为左(0,2)和右(3,4)合并到整个
左边分为(0,1)(1,2)右边只能分为(3,4)
(0,1)排序
(1,2)排序
(3,4)排序
将左边的联合到,再结合右边的
5.快速排序
我们从数组中选择一个元素,我们把这个元素称之为中轴元素吧,然后把数组中所有小于中轴元素的元素放在其左边,所有大于或等于中轴元素的元素放在其右边,显然,此时中轴元素所处的位置的是有序的。也就是说,我们无需再移动中轴元素的位置。
从中轴元素那里开始把大的数组切割成两个小的数组(两个数组都不包含中轴元素),接着我们通过递归的方式,让中轴元素左边的数组和右边的数组也重复同样的操作,直到数组的大小为1,此时每个元素都处于有序的位置。
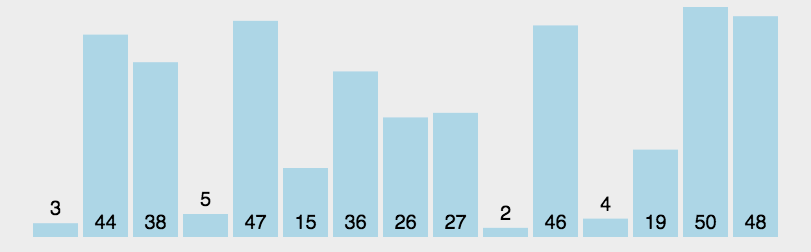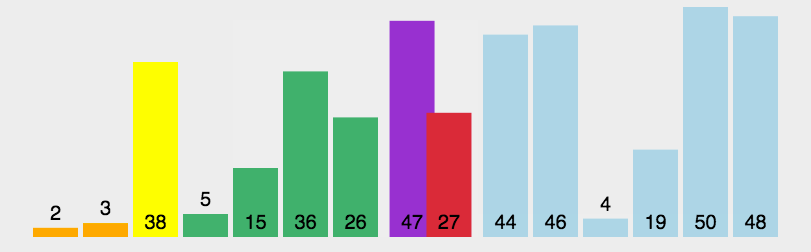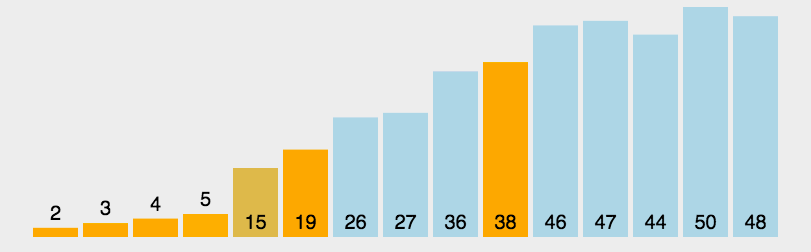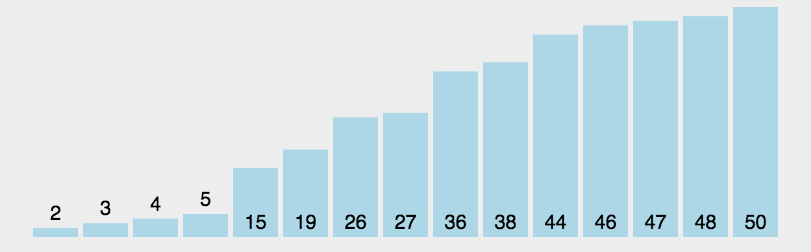
代码
public static void main(String[] args) {
int[] arr = {1,23,4,2,5,2,6,8,8};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
quickSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
public static void quickSort(int [] arr){
if(arr==null||arr.length<2){
return;
}
quickSort(arr,0,arr.length-1);
}
//arr[l...r]排好序
public static void quickSort(int[] arr,int L,int R){
if(L<R){
swap(arr,(int)(Math.random()*(R-L+1)),R);
int[] p = partition(arr,L,R);
quickSort(arr,L,p[0]-1);//<区
quickSort(arr,p[1]+1,R);//>区
}
}
//这是一个处理arr[l...r]的函数,以arr[R]这个值作为划分依据,分为大于arr[R],等于arr[R],小于arr[R]的区域
//返回等于区域(左边界,右边界),所以返回的是一个长度为2的数组res,res[0],res[1]
public static int[] partition(int[] arr,int L,int R){
int less = L - 1;//<区,右边界
int more = R;//>区 左边界
while(L<more){//遍历整个地址
if(arr[L] < arr[R]){ //当前数小于划分值
less++;
swap(arr,less,L);
L++;
// swap(arr,++less,L++);
}else if(arr[L] > arr[R]){ //当前数大于划分值
more--;
swap(arr,more,L);
// swap(arr,--more,L);
}else{
L++;
}
}
swap(arr,more,R);
return new int[]{less+1,more};
}
/**
* 交换数组i位置和j位置的值
* @param arr
* @param i
* @param j
*/
public static void swap(int[] arr,int i,int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
课后习题:
习题:
荷兰国旗
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。要求额外空间复杂度O(1),时间复杂度 O(N)
/**
* 题目描述
* 给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。要求额外空间复杂度O(1),时间复杂度 O(N)
*/
public static void code01(int[] arr,int num){
if(arr.length<=2)
return ;
partition(arr,num);
}
/**
* 设定一个小于等于区,从0开始比较,如果当前数字小于等于num ,让其与小于等于区的下一个值做交换,再将小于等于区扩大一位,
* 直到将所有的数字都与num进行过比较。重新排好的数组就是所求的数组
* @param arr
* @param num
*/
public static void partition(int[] arr,int num){
int less = 0;//设定一个小于等于区,这个区域-1的位置都是小于等于num的数字
for (int i = 0; i < arr.length; i++) {//从0开始比较,直到将所有的数字都与num进行过比较。
if(arr[i]<=num){//如果当前数字小于等于num
swap(arr,less,i);//让其与小于等于区的下一个值做交换
less++;//将小于等于区扩大一位
}
}
}
/**
* 另一种写法
* 设定一个小于等于区,从-1开始比较,如果当前数字小于等于num ,将小于等于区扩大一位,让其与小于等于区的内容做交换
* 直到将所有的数字都与num进行过比较。重新排好的数组就是所求的数组
* @param arr
* @param num
*/
public static void partition2(int[] arr,int num){
int less = -1;//设定一个小于等于区,这个区域-1的位置都是小于等于num的数字
for (int i = 0; i < arr.length; i++) {//从0开始比较,直到将所有的数字都与num进行过比较。
if(arr[i]<=num){//如果当前数字小于等于num
less++;//将小于等于区扩大一位
swap(arr,less,i);//让其与小于等于区的下一个值做交换
}
}
}
public static void swap(int[] arr,int L,int R){
arr[L] = arr[L]^arr[R];
arr[R] = arr[L]^arr[R];
arr[L] = arr[L]^arr[R];
}
整个算法的经典之处
arr[i] <= num arr[i] 和 小于等于区的下一个数交换,小于等于区右扩,i++
arr[i] > num i++
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边。要求额外空间复杂度O(1),时间复杂度O(N)
/**
* 定一个数组arr, 和一个数num, 请把小于等于num的数放在数组的左边,等于num的放中间,大于num的数放在数组的右边。要求:额外空间复杂度O(1),时间复杂度O(n)。
*/
public static void code02(int[] arr,int num){
if(arr.length<=2)
return ;
partition(arr,0,arr.length-1,num);
}
/**
* @param arr 数组
* @param left 左边
* @param right 右边
* @param num 大于小于等于的值
*/
public static void partition(int[] arr,int left,int right,int num){
int L = left -1;
int R = right+1;
for (int i = 0; i < arr.length;) {
if(arr[i]<num){//当前值和小于区下一个(++)交换,小于区右扩,i++
L++;
swap(arr,i,L);
i++;
}else if(arr[i]>num){//当前值和大于区前一个(--)交换,大于区右扩,i不变
R--;
swap(arr,i,R);
}else{//等于num i++
i++;
}
}
}
public static void swap(int[] arr,int L,int R){
arr[L] = arr[L]^arr[R];
arr[R] = arr[L]^arr[R];
arr[L] = arr[L]^arr[R];
}
/**
* while循环的写法
* @param arr
* @param left
* @param right
* @param num
*/
public static void partition2(int[] arr,int left,int right,int num){
int L = left -1;
int R = right+1;
int cur = left;
while(cur<R){
if(arr[cur]<num){//当前值和小于区下一个交换,小于区右扩,i++
++L;
swap(arr,cur,L);
++cur;
}else if(arr[cur]>num){//当前值和大于区前一个交换,大于区右扩,i不变
--R;
swap(arr,cur,R);
}else{//等于num i++
cur++;
}
}
}
算法的经典之处
arr[i]<num 当前值和小于区下一个交换,小于区右扩,i++
arr[i]>num 当前值和大于区前一个交换,大于区右扩,i不变
arr[i]=num i++
6.计数排序
计数排序是一种适合于最大值和最小值的差值不是不是很大的排序。
基本思想:就是把数组元素作为数组的下标,然后用一个临时数组统计该元素出现的次数,例如 temp[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到大汇总起来,此时汇总起来是数据是有序的。

public static void main(String[] args) {
int[] arr = {1,4,2,5,2,6,8,8};
System.out.println("排序前:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
int[] arr2 = countSort(arr);
System.out.println("排序后:");
for (int i = 0; i < arr2.length; i++) {
System.out.print(arr2[i]+" ");
}
System.out.println();
}
/**
* 计数排序
* @param arr
* @return
*/
public static int[] countSort(int[] arr){
int[] temp = new int[10];
for (int a : arr) {
temp[a]++;
}
int[] result = new int[arr.length];
int r = 0;
for (int i = 0; i < temp.length; i++) {
while (temp[i]>0){
result[r]=i;
r++;
temp[i]--;
}
}
return result;
}
7.堆排序
1.堆就是用数组实现的完全二叉树结构
数组获取某个二叉树的
左孩子(2i+1)
右孩子(2i+2)
父节点((i-1)/2)
i为要获取的节点的数组下标
3 5 2 7 1 9 6
3
5 2
7 1 9 6
5的左节点2*1+1,arr[3]=7
5的右节点2*1+2,arr[4]=1
5的父节点(1-1)/2,arr[0]=3
2.完全二叉树中如果每颗子树的最大值都在顶部就是大根堆
3.完全二叉树中如果每颗子树的最小值都在顶部就是小根堆
父节点是最大值是大根堆,相反小根堆
public static void heapSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
for (int i = 0; i < arr.length; i++) {//O(N)
heapInsert(arr,i);//O(logN)
}
int heapSize = arr.length;
swap(arr,0,--heapSize);
while (heapSize > 0){//O(N)
heapify(arr,0,heapSize);//O(logN)
swap(arr,0,--heapSize);//O(1)
}
}
/**
* 某个位置现在处在index的位置,往上继续移动
* @param arr
* @param index
*/
public static void heapInsert(int[] arr,int index){
while(arr[index] > arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}
//某个数在index位置,能否往下移动
public static void heapify(int[] arr,int index,int heapSize){
int left = index * 2 + 1;//左孩子下标
while( left < heapSize ){//下方还有孩子的时候
//下标的两个孩子,谁的值最大,把下标给largest
int largest = left+1 < heapSize && arr[left+1] > arr[left] ? left+1 : left;
//父和孩子之间,谁的值大,把下标给largest
largest = arr[largest] > arr[index] ? largest : index;
if(largest == index){
break;
}
swap(arr,largest,index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr,int i,int j){
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
另一种写法
public static void heapSort(int[] arr){
if(arr==null||arr.length<2){
return;
}
/* for (int i = 0; i < arr.length; i++) {
heapInsert(arr,i);
}*/
//生成大根堆最快的方法
for(int i=arr.length-1;i>=0;i--){
heapify(arr,i,arr.length);
}
int heapSize = arr.length;
swap(arr,0,--heapSize);
while (heapSize > 0){
heapify(arr,0,heapSize);
swap(arr,0,--heapSize);
}
}
4.堆结构的heapInsert与heapify操作
heapInsert操作,将左边的内容一直从大到小排列
/**
* 某个位置现在处在index的位置,往上继续移动
* @param arr
* @param index
*/
public static void heapInsert(int[] arr,int index){
while(arr[index] > arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}
heapify操作,父节点,左节点,右节点中的最大的值
//某个数在index位置,能否往下移动
public static void heapify(int[] arr,int index,int heapSize){
int left = index * 2 + 1;//左孩子下标
while( left < heapSize ){//下方还有孩子的时候
//下标的两个孩子,谁的值最大,把下标给largest
int largest = left+1 < heapSize && arr[left+1] > arr[left] ? left+1 : left;
//父和孩子之间,谁的值大,把下标给largest
largest = arr[largest] > arr[index] ? largest : index;
if(largest == index){
break;
}
swap(arr,largest,index);
index = largest;
left = index * 2 + 1;
}
}
5.堆结构的增大和减小
6.优先级队列结构,就是堆结构
8.桶排序(计数排序和基数排序的基础)
桶排序思想下的排序
1.计数排序
2.基数排序
分析:
1.桶排序思想下的排序都是不基于比较的排序。
2.时间复杂度为O(N),额外空间负载度O(N)。
3.应用范围有限,需要样本的数据状况满足桶的划分。
9.基数排序
基数排序的排序思路是这样的:先以个位数的大小来对数据进行排序,接着以十位数的大小来多数进行排序,接着以百位数的大小……
排到最后,就是一组有序的元素了。不过,他在以某位数进行排序的时候,是用“桶”来排序的。
由于某位数(个位/十位….,不是一整个数)的大小范围为0-9,所以我们需要10个桶,然后把具有相同数值的数放进同一个桶里,之后再把桶里的数按照0号桶到9号桶的顺序取出来,这样一趟下来,按照某位数的排序就完成了

public class RadioSort {
public static void main(String[] args) {
int[] arr = {5, 3, 6, 8, 100, 7, 9, 4, 20};
sort(arr);
}
public static int[] sort(int[] arr) {
if(arr==null||arr.length==2) {
return arr;
}
int max = findMax(arr);
int num = 1;
while (max/10>0){
max= max/10;
num++;
}
List<List<Integer>> totalBucket = new LinkedList<>();
//初始化桶
for (int i = 0; i < 10; i++) {
totalBucket.add(new LinkedList<Integer>());
}
for (int i = 0; i < num; i++) {
//放入对应的桶
for (int j = 0; j < arr.length; j++) {
int location = (arr[j] / (int)Math.pow(10,i)) % 10;
totalBucket.get(location).add(arr[j]);
}
int k = 0;
for (List<Integer> integers : totalBucket) {
for (Integer integer : integers) {
arr[k++]=integer;
}
integers.clear();
}
}
return arr;
}
public static int findMax(int[] arr) {
int max = arr[0];
for (int i : arr) {
if(i>max){
max = i;
}
}
return max;
}
}
比较器
1.比较器的实质就是重载比较运算符
2.比较器可以很好的应用在特殊标准的排序上。
3.比较器可以很好的应用在根据特殊标准的结构上。
public static void main(String[] args) {
Student student1 = new Student("A", 2, 20);
Student student2 = new Student("B", 1, 30);
Student student3 = new Student("C", 3, 32);
Student[] students = {student1, student2, student3};
Arrays.sort(students,new IdAscendingComparator());
for (int i = 0; i < students.length; i++) {
System.out.println(students[i]);
}
}
public static class IdAscendingComparator implements Comparator<Student> {
/**
* 返回负数的时候,第一个参数排到前面
* 返回正数的时候,第二个参数排到前面
* 返回0的时候,谁在前面无所谓
*/
@Override
public int compare(Student o1, Student o2) {
if(o1.getId() < o2.getId()){
return -1;
}
if(o1.getId() > o2.getId()){
return 1;
}
return 0;
}
}
class Student{
private String name;
private int id;
private int age;
public Student(String name, int id, int age) {
this.name = name;
this.id = id;
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"name='" + name + '\'' +
", id=" + id +
", age=" + age +
'}';
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
}
public class Code06_smallgendui {
public static void main(String[] args) {
PriorityQueue<Integer> heap = new PriorityQueue<>(new Acomp());//小根堆
heap.add(6);
heap.add(9);
heap.add(3);
heap.add(2);
heap.add(10);
while (!heap.isEmpty()){
System.out.println(heap.poll());
}
}
}
class Acomp implements Comparator<Integer>{
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
}
排序算法的比较