一、概述

时域信号经FFT变换后得到了频谱，在绘制频谱图时还必须设置正确的频率刻度，这样才能从图中得到正确的结果。

二、实例分析

有一余弦信号，信号频率为30Hz，采样频率128Hz，信号长128，原始信号如下图所示：
Matlab代码如下:

fs=128;                         % 采样频率
N=128;                          % 信号长度
t=(0:N-1)/fs;                   % 时间序列
y=cos(2*pi*30*t);               % 余弦信号
figure,plot(y,'r'); xlabel('样点'); ylabel('幅值');

图1 原始信号

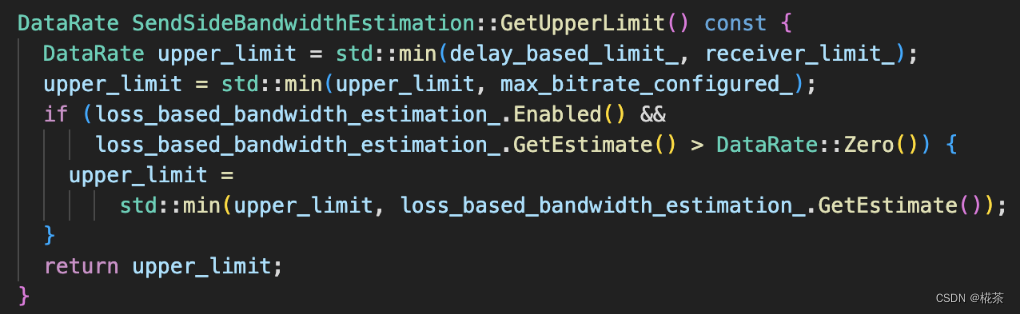
如果不对频谱刻度进行处理，而直接作图显示频谱，那么得到的频谱值会有所偏差，如下图所示：可知信号频谱为30Hz，而实际求出的频谱为31Hz，发生这种错误的原因是频率刻度的设置错误。

y=fft(y,N);                     % FFT
figure,stem(abs(y),'r');title('频谱')

图2 频谱图

三、频谱刻度设置方法

信号长为N，采样频率为fs，在DFT(FFT)以后信号的频率在-fs/2和fs/2之间，谱线之间的频率间隔为：

$$\Delta f=\frac{f_s}{N}=\frac{1}{N{T}_s}$$

式中： $T_s$是采样周期。频率刻度从0开始，最大频率为 $\frac{f_s}{2}$。因此，频谱刻度简单设置如下式所示：

$$freq=(0:N-1)\times \frac{f_s}{N}$$

给出的频率刻度为0，△f,···， $\frac{f_s}{2}$，fs-△f，但实际不存在大于 $\frac{f_s}{2}$的频率分量，大于 $\frac{f_s}{2}$的频率分量实际是负频率的分量。如图3所示。

为了给出从负频率到正频率的全部分量，频率刻度应为

$$freq=(0:N-1)\times \frac{f_s}{N}-\frac{f_s}{2}$$

这样给出的频率刻度是: $-\frac{f_s}{2}-\frac{f_s}{2}+\Delta f,\cdot \cdot \cdot ,0,\Delta f,\cdot \cdot \cdot ,\frac{f_s}{2}-\Delta f$

图3 正负频率对比

3.1 正负频谱刻度设置

按照上述理论的设置，对应的matlab代码如下式所示：

%% 频谱显示1(正负频谱都显示)
freq0=(0:N-1)*fs/N;              % 频率间隔
figure,plot(freq0,abs(y),'r')    % 频谱

图4 频谱刻度设置(正负频率同时显示)

3.2 正频谱刻度设置

也可以通过上式只显示正频率：对应的Matlab代码如下：

%% 频谱显示2(正频谱)
freq=(0:N/2)*fs/N;              % 设置正频率刻度 
figure,plot(freq,abs(y(1:N/2+1)),'r');title('只有正频率刻度')
figure,stem(freq,abs(y(1:N/2+1)),'r');title(' 只有正频率刻度')

图5 频谱刻度设置(正频率)

3.3 通过linspace函数设置频率刻度(正、负频率都显示)

也可以通过linspace函数设置频率刻度，对应Matlab代码如下：

freq3=linspace(0,fs,N+1)-fs/2;     % linspace 函数设置正负频率
freq3=freq3(1:N);
figure,plot(freq3,abs(y),'r')    % 频谱

图6 频谱刻度设置(正负频率同时显示)

3.4 通过linspace函数设置频率刻度(正频率)

或者通过linspace函数设置频率刻度显示正频率

%% 通过linspace函数设置频率刻度(正频率)
freq4=linspace(0,fs/2,N/2+1);     % linspace 函数设置正负频率
figure,stem(freq4,abs(y(1:N/2+1)),'r');title('正频率刻度')

图7 频谱刻度设置(正频率)

四、Matlab程序获取与验证

代码也可从以下链接处获取：

频谱图中频率刻度设置

可开展针对性验证实验，请私信博主。