机器学习12：分类 Classification

分类（Classification）是一个有监督的学习过程，目标数据集（示例集）中具有的类别是已知的，分类过程需要做的就是把每一条记录归到对应的类别下。由于必须事先知道各个类别的信息，并且所有待分类的数据条目都默认有对应的类别，因此分类算法也有其局限性，当上述条件无法满足时，我们就需要尝试聚类（后面介绍）分析。

在【机器学习11】中，笔者介绍了逻辑回归（Logistic Regression），它就是一种分类分析，它有正向类和负向类，即：y ∈ {0, 1}，其中 0 代表负向类，1 代表正向类。

当面对一个分类问题：y = 0 或 1，可能出现的情况是： hθ(x) > 1 或 < 0，就无法进行结果的归纳。此时就需要采用逻辑回归，得到的结果可以满足： 0≤ hθ(x) ≤1 。可以说逻辑回归是一种特殊的分类算法，同理，更普遍的分类算法中可能有更多的类别，即：y ∈ {0, 1, 2, 3 ...} 。

1. 阈值 Thresholding

2.混淆矩阵

3.准确性 Accuracy

4.精确度和召回率: Precision and Recall

4.1 精确度

4.2 召回率

4.3 精确度和召回率：一场拉锯战

5.ROC 曲线和 AUC

5.1 ROC曲线

5.2 AUC：ROC 曲线下的面积

6.预测偏差

6.1 分桶和预测偏差

7.参考文献

1. 阈值 Thresholding

在【机器学习11】中，我们介绍了逻辑回归。逻辑回归返回一个概率，我们可以 “按原样” 使用返回的概率（例如，用户点击此广告的概率为 0.00023），也可以将返回的概率转换为二进制值（例如，这封电子邮件是垃圾邮件（或者不是垃圾邮件））。

对于某一电子邮件，如果逻辑回归模型返回的预测结果为 0.9995，那么，该电子邮件很可能是垃圾邮件。相反，在同一逻辑回归模型上预测得分为 0.0003 的另一封电子邮件很可能不是垃圾邮件。但是，对于预测分数为 0.6 的电子邮件又该如何区分呢？

为了将逻辑回归值映射到二元类别，我们必须定义 分类阈值（也称为决策阈值）。高于该阈值的值表示“垃圾邮件”；低于阈值表示 “不是垃圾邮件”。人们很容易假设分类阈值应始终为 0.5，但阈值取决于问题，因此是必须调整的值。

以下部分将详细介绍可用于评估分类模型预测的指标，以及更改分类阈值对这些预测的影响。

注意：“调整”逻辑回归的阈值与调整学习率等超参数不同。选择阈值时需要充分评估犯错误而遭受的损失，举个例子，错误地将非垃圾邮件标记为垃圾邮件是非常糟糕的。然而，错误地将垃圾邮件标记为非垃圾邮件虽然令人不快，但影响要小得多。

2.混淆矩阵

在本节中，我们将定义用于评估分类模型的指标的主要方法。首先，先讲一个寓言：

伊索寓言：狼来了（压缩版）

一个牧童厌倦了照料镇上的羊群。为了好玩，他大喊：“狼来了！” 即使看不见狼。村民们跑去保护羊群，但当他们意识到男孩在跟他们开玩笑时，他们非常生气。

[将上一段重复N次。]

一天晚上，牧童看到一只真正的狼靠近羊群，大声喊道：“狼来了！” 村民们拒绝再受愚弄，留在自己的房子里。饿狼把羊群变成了羊排。小镇挨饿了。恐慌随之而来。

让我们做出以下定义：

“有狼”是一个正类。
“无狼”是一个负类。

我们可以使用描述所有四种可能结果的：2x2混淆矩阵来总结我们的“狼预测”模型：

真阳性 (TP)：现实：狼来了牧童说：“狼来了” 结果：牧羊人是英雄。	假阳性 (FP)：现实：狼没有来牧童说：“狼来了” 结果：村民对牧童叫醒他们感到愤怒。
假阴性（FN）：现实：狼来了牧童说：没有狼。结果：狼吃掉了所有的羊。	真阴性 (TN)：现实：狼没有来牧童说：没有狼。结果：每个人都很好。

真正的阳性是模型正确预测阳性类别的结果。同样，真正的负例是模型正确预测负类的结果。假阳性是模型错误地预测阳性类别的结果。假阴性是模型错误地预测阴性类别的结果。在以下部分中，我们将了解如何使用从这四种结果派生的指标来评估分类模型。

3.准确性 Accuracy

准确性是评估分类模型的指标之一。通俗地说， 准确性是我们的模型正确预测的比例。准确度的正式定义如下：

$\text{Accuracy} = \frac{\text{Number of correct predictions}}{\text{Total number of predictions}}$

对于二元分类，准确率也可以按照正数和负数来计算，如下所示：

$\text{Accuracy} = \frac{TP+TN}{TP+TN+FP+FN}$

其中TP = 真阳性，TN = 真阴性，FP = 假阳性，FN = 假阴性。

让我们尝试计算以下模型的准确率，该模型将 100 个肿瘤分类为恶性（正类）或良性（负类）：

真阳性 (TP)：现实：恶性 ML 模型预测：恶性 TP结果数量：1	假阳性 (FP)：现实：良性 ML 模型预测：恶性 FP 结果数量：1
假阴性（FN）：现实：恶性 ML 模型预测：良性 FN 结果数量：8	真阴性 (TN)：现实：良性 ML 模型预测：良性 TN 结果数量：90

$\text{Accuracy} = \frac{TP+TN}{TP+TN+FP+FN} = \frac{1+90}{1+90+1+8} = 0.91$

准确率达到 0.91，即 91%（总共 100 个示例中有 91 个预测正确）。这意味着我们的肿瘤分类器在识别恶性肿瘤方面做得很好吗？并非如此。

在实际应用中，我们需要对积极因素和消极因素进行更仔细的分析，以更深入地了解我们模型的性能。在 100 个肿瘤实例中，91 个为良性（90 个 TN 和 1 个 FP），9 个为恶性（1 个 TP 和 8 个 FN）。在 91 个良性肿瘤中，该模型正确地将 90 个识别为良性肿瘤。那挺好的。然而，在 9 种恶性肿瘤中，该模型仅正确地将 1 种识别为恶性——这是一个可怕的结果，因为 9 种恶性肿瘤中有 8 种未被诊断出来！

虽然 91% 的准确度乍一看似乎不错，但另一个始终预测良性的肿瘤分类器模型在我们的示例中将达到完全相同的准确度（91/100 正确的预测）。换句话说，我们的模型并不比区分恶性肿瘤和良性肿瘤的预测能力为零的模型更好。

当您处理类别不平衡的数据集（例如这个数据集）时，仅靠准确性并不能说明全部情况，其中正标签和负标签的数量之间存在显着差异。

在下一节中，我们将研究评估类别不平衡问题的两个更好的指标：精确度和召回率。

4.精确度和召回率: Precision and Recall

4.1 精确度

Precision 试图回答以下问题：

阳性识别中真正正确的比例是多少？

精度定义如下：

$\text{Precision} = \frac{TP}{TP+FP}$

注意：不产生误报的模型的精度为 1.0。

让我们计算上一节分析肿瘤的 ML 模型的精度：

真阳性 (TP)：1	假阳性 (FP)：1
漏报 (FN)：8	真阴性 (TN)：90

$\text{Precision} = \frac{TP}{TP+FP} = \frac{1}{1+1} = 0.5$

我们的模型的精度为 0.5，换句话说，当它预测肿瘤是恶性时，它的正确率是 50%。

4.2 召回率

回顾上文，我们来思考一个问题：

正确识别的实际阳性比例是多少？

从数学上讲，召回率定义如下：

$\text{Recall} = \frac{TP}{TP+FN}$

注意：不产生假阴性的模型的召回率为 1.0。

让我们计算肿瘤分类器的召回率：

真阳性 (TP)：1	误报 (FP)：1
漏报 (FN)：8	真阴性 (TN)：90

$\text{Recall} = \frac{TP}{TP+FN} = \frac{1}{1+8} = 0.11$

我们的模型的召回率为 0.11，换句话说，它正确识别了 11% 的恶性肿瘤。

4.3 精确度和召回率：难以兼得

要全面评估模型的有效性，必须检查精确度和召回率。不幸的是，精确度和召回率常常处于矛盾状态。也就是说，提高精确度通常会降低召回率，反之亦然。通过查看下图来探索这个概念，该图显示了电子邮件分类模型做出的 30 个预测。分类阈值右侧的邮件被分类为“垃圾邮件”，而左侧的邮件被分类为“非垃圾邮件”。

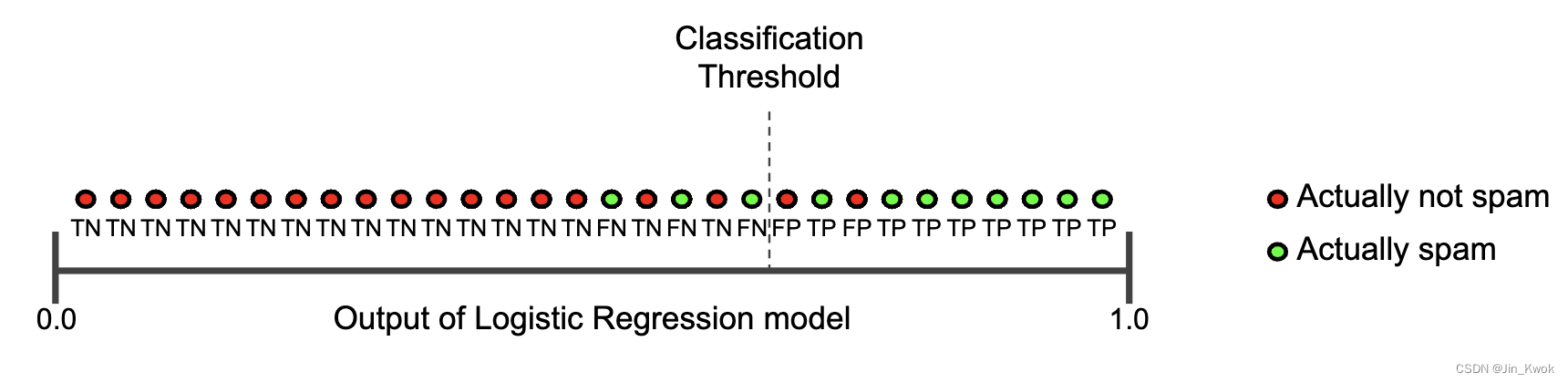图 1. 将电子邮件分类为垃圾邮件或非垃圾邮件

我们根据图 1 所示的结果来计算精确率和召回率：

真阳性 (TP)：8	误报 (FP)：2
漏报 (FN)：3	真阴性 (TN)：17

精度衡量的是被标记为垃圾邮件并被正确分类的电子邮件的百分比，即图 1 中阈值线右侧绿色点的百分比：

$\text{Precision} = \frac{TP}{TP + FP} = \frac{8}{8+2} = 0.8$

召回率衡量的是被正确分类的实际垃圾邮件的百分比，即图 1 中阈值线右侧绿点的百分比：

$\text{Recall} = \frac{TP}{TP + FN} = \frac{8}{8 + 3} = 0.73$

图 2 说明了增加分类阈值的效果。

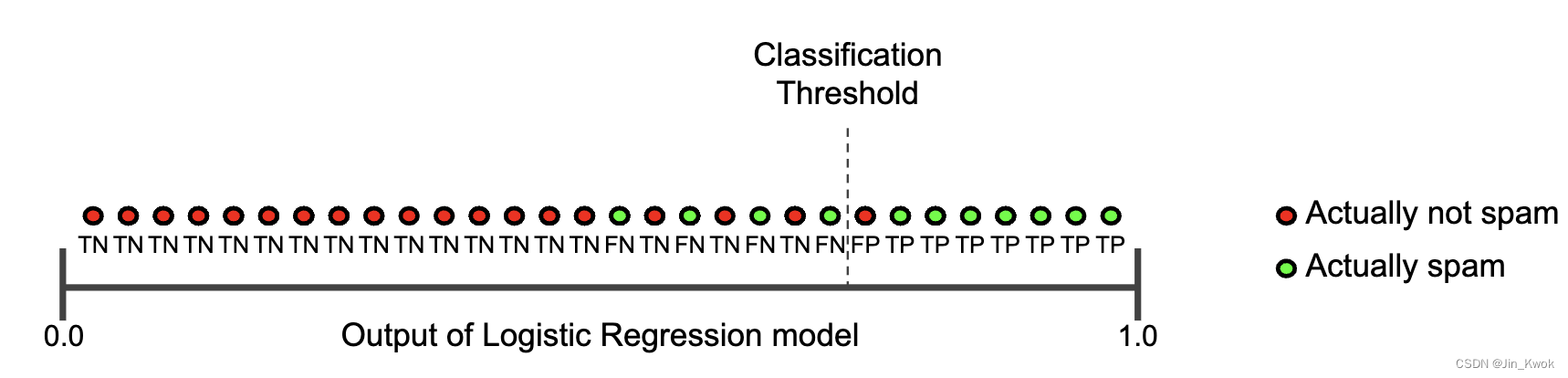图 2. 增加分类阈值

假阳性数量减少，但假阴性数量增加。结果，准确率提高，而召回率降低：

真阳性 (TP)：7	误报 (FP)：1
漏报 (FN)：4	真阴性 (TN)：18

$\text{Precision} = \frac{TP}{TP + FP} = \frac{7}{7+1} = 0.88$

$\text{Recall} = \frac{TP}{TP + FN} = \frac{7}{7 + 4} = 0.64$

相反，图 3 说明了降低分类阈值（从图 1 中的原始位置）的效果。

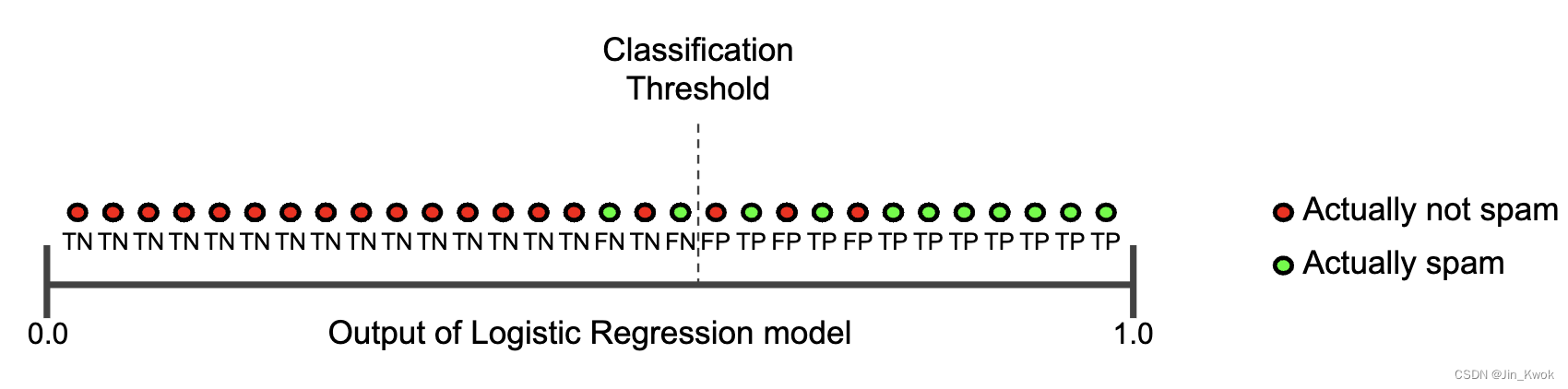图 3. 降低分类阈值

假阳性增加，假阴性减少。结果，这一次，准确率下降，召回率增加：

真阳性 (TP)：9	误报 (FP)：3
漏报 (FN)：2	真阴性 (TN)：16

$\text{Precision} = \frac{TP}{TP + FP} = \frac{9}{9+3} = 0.75$

$\text{Recall} = \frac{TP}{TP + FN} = \frac{9}{9 + 2} = 0.82$

5.ROC 曲线和 AUC

5.1 ROC曲线

ROC 曲线是显示分类模型在所有分类阈值下的性能的图表。该曲线绘制了两个参数：

真阳性率
误报率

真阳性率( TPR ) 是召回率的同义词，因此定义如下：

$TPR = \frac{TP} {TP + FN}$

误报率( FPR ) 定义如下：

$FPR = \frac{FP} {FP + TN}$

ROC 曲线绘制了不同分类阈值下的 TPR 与 FPR。降低分类阈值会将更多项目分类为阳性，从而增加假阳性和真阳性。下图显示了典型的 ROC 曲线。

图 4. 不同分类阈值下的 TP 与 FP 率

为了计算 ROC 曲线中的点，我们可以使用不同的分类阈值多次评估逻辑回归模型，但这效率很低。幸运的是，有一种高效的、基于排序的算法可以为我们提供这些信息，称为 AUC。

5.2 AUC：ROC 曲线下的面积

AUC 代表“ROC 曲线下的面积”。也就是说，AUC 测量整个 ROC 曲线（考虑积分）下方从 (0,0) 到 (1,1) 的整个二维区域。

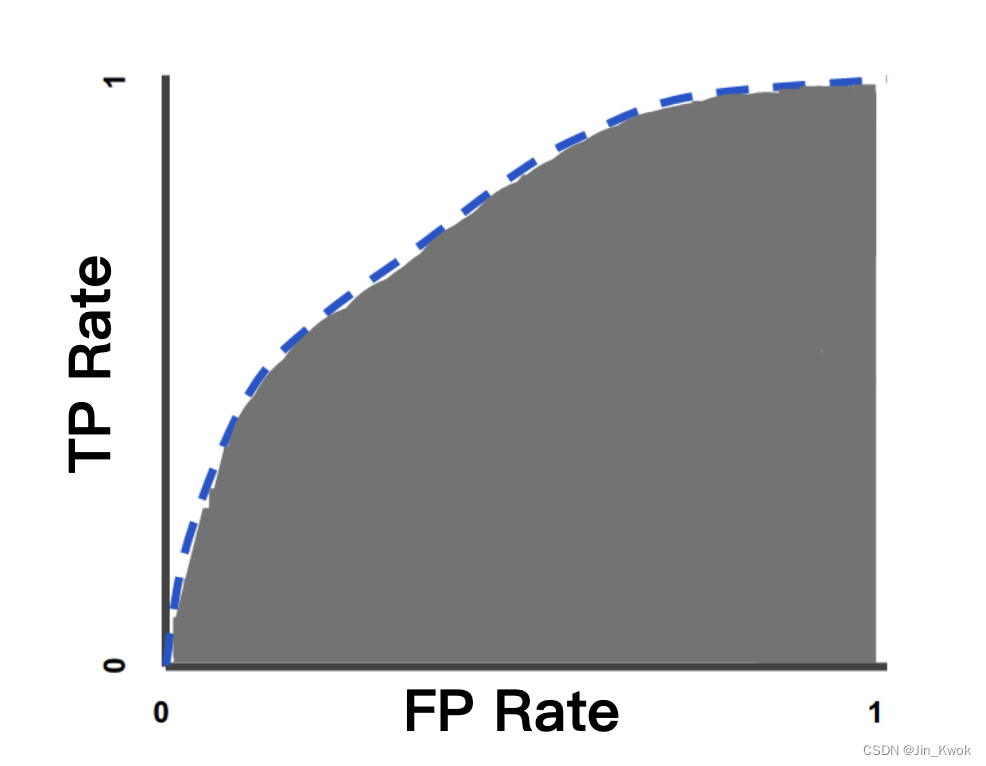
图 5.AUC（ROC 曲线下面积）

AUC 提供了所有可能的分类阈值的总体性能衡量标准。解释 AUC 的一种方法是模型对随机正例的排名高于随机负例的概率。例如，给出以下示例，它们按逻辑回归预测的升序从左到右排列：

图 6. 预测按逻辑回归分数升序排列

AUC 表示随机正（绿色）示例位于随机负（红色）示例右侧的概率。AUC 的值范围为 0 到 1。预测 100% 错误的模型的 AUC 为 0.0；预测 100% 正确的人的 AUC 为 1.0。

AUC 之所以理想，有以下两个原因：

AUC 是尺度不变的。它衡量的是预测的排名，而不是它们的绝对值。
AUC 是分类阈值不变的。无论选择什么分类阈值，它都会衡量模型预测的质量。

然而，上述两个原因都带有警告，它们可能会限制 AUC 在某些用例中的有用性：

尺度不变性并不总是可取的。例如，有时我们确实需要经过良好校准的概率输出，而 AUC 不会告诉我们这一点。
分类阈值不变性并不总是理想的。如果假阴性与假阳性的成本存在巨大差异，则最小化一种类型的分类错误可能至关重要。例如，在进行垃圾邮件检测时，您可能希望优先考虑最大限度地减少误报（即 FP，会将正常邮件误判为垃圾邮件，可能因此错过重要信息）。对于此类优化，AUC 并不是一个有用的指标。

6.预测偏差

逻辑回归预测应该是无偏的。那是：

“预测平均值” 应该 ≈ “观测平均值”

预测偏差是衡量这两个平均值相差多远的量。那是：

$\text{prediction bias} = \text{average of predictions} - \text{average of labels in data set}$

注意： “预测偏差” 与偏差（ wx + b 中的 b ）的含义是不同的。

非零预测偏差意味着模型中的某个地方存在错误，因为它表明模型对于正标签出现的概率的预测是错误的。例如，假设我们知道平均有 1% 的电子邮件是垃圾邮件，如果我们对给定电子邮件一无所知，我们应该预测它有 1% 的可能性是垃圾邮件。同样，一个好的垃圾邮件模型应该平均预测电子邮件有 1% 的可能性是垃圾邮件。（换句话说，如果我们对每封电子邮件为垃圾邮件的预测可能性进行平均，结果应为 1%。）如果相反，模型的平均预测为垃圾邮件的可能性为 20%，我们可以得出结论，它表现出预测偏差。

预测偏差的可能根本原因如下：

特征集不完整
数据集存在噪声
有偏差的训练样本
正则化过强

在实践中，有些工程师会试图通过对学习模型进行后处理来纠正预测偏差，即通过添加一个校准层来调整模型的输出以减少预测偏差。例如，如果模型有 +3% 的偏差，则可以添加一个校准层，将平均预测降低 3%。然而，添加校准层并不是一个好主意，原因如下：

掩盖问题，解决的是症状而不是原因。
增加了系统的复杂度，使得系统更加脆弱。

如果可能，应避免使用校准层。使用校准层的项目往往会变得依赖它们——使用校准层来修复模型的所有缺陷。最终，维护校准层可能会成为一场噩梦。

注意：好的模型通常具有接近于零的偏差。也就是说，低预测偏差并不能证明你的模型是好的。一个非常糟糕的模型可能具有零预测偏差。例如，尽管偏差为零，但仅预测所有示例的平均值的模型将是一个糟糕的模型。

6.1 分桶和预测偏差

逻辑回归预测 0 到 1之间的值。但是，所有带标签的示例要么恰好为 0（例如，表示“非垃圾邮件”），要么正好为 1（例如，表示“垃圾邮件”）。因此，在考察预测偏差时，仅凭一个样本并不能准确判断预测偏差；您必须检查“桶”示例的预测偏差。也就是说，只有当将足够多的示例分组在一起以便能够将预测值（例如，0.392）与观察值（例如，0.394）进行比较时，逻辑回归的预测偏差才有意义。

您可以通过以下方式形成桶：

线性分解目标预测。
形成分位数。

考虑以下特定模型的校准图。每个点代表一桶 1,000 个值。各轴的含义如下：

x 轴表示模型为该存储桶预测的平均值。
y 轴表示该存储桶的数据集中值的实际平均值。

两个轴都是对数刻度。

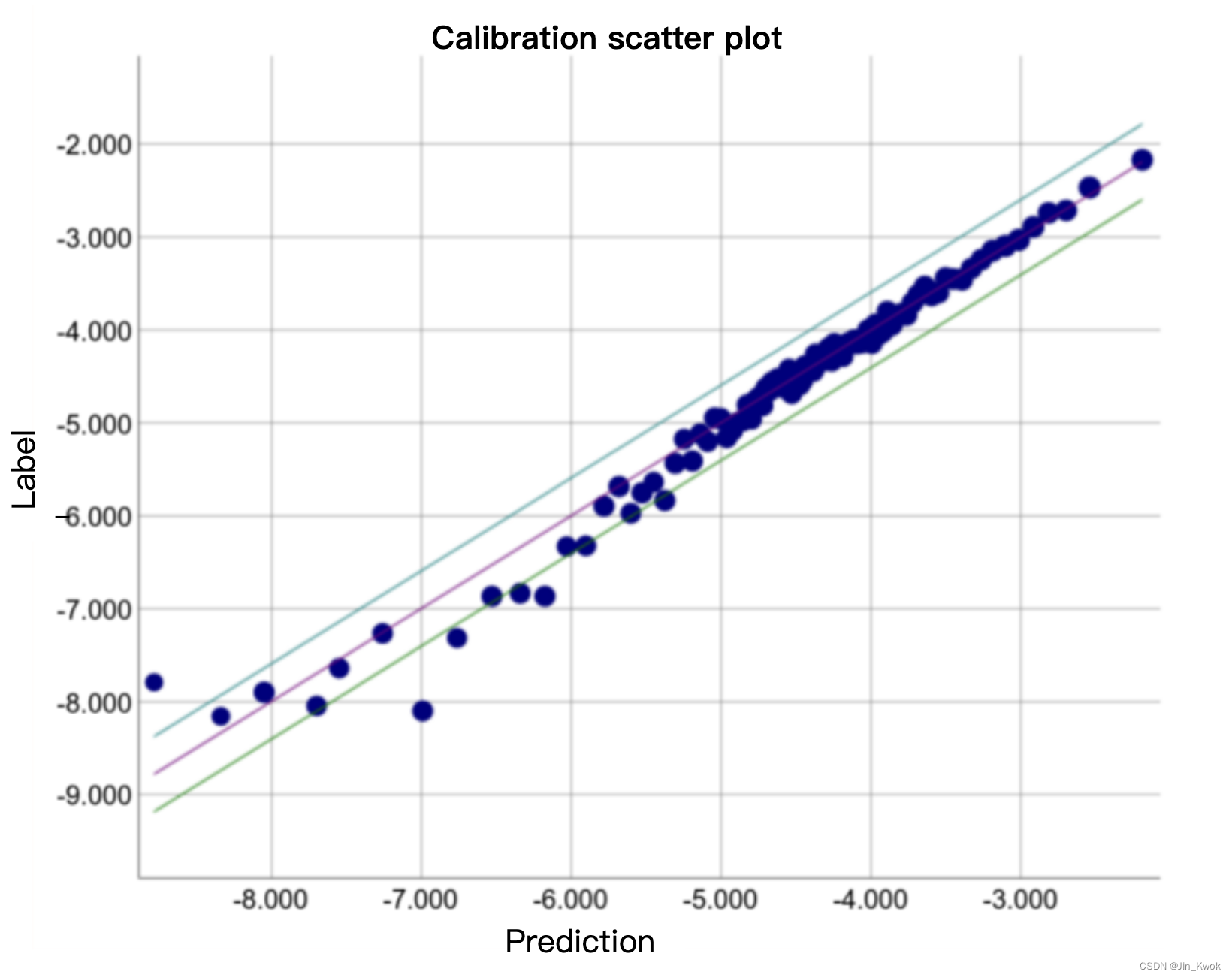
图 8. 预测偏差曲线（对数刻度）

为什么模型的部分预测结果如此糟糕？以下是一些可能性：

训练集不能充分代表数据空间的某些子集。
数据集的某些子集比其他子集噪声更大。
该模型过于正则化。（考虑减小 lambda 的值。）

7.参考文献

链接-https://developers.google.cn/machine-learning/crash-course/classification/video-lecture

真阳性 (TP)：现实：狼来了牧童说：“狼来了” 结果：牧羊人是英雄。	假阳性 (FP)：现实：狼没有来牧童说：“狼来了” 结果：村民对牧童叫醒他们感到愤怒。
假阴性（FN）：现实：狼来了牧童说：没有狼。结果：狼吃掉了所有的羊。	真阴性 (TN)：现实：狼没有来牧童说：没有狼。结果：每个人都很好。