1 坐标系
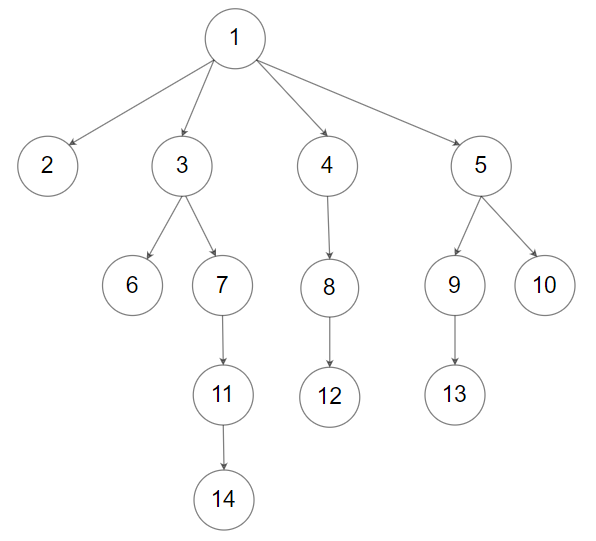
- 大多数计算机屏幕采用的坐标系是以左上角为原点,水平(右)为x轴,纵向(下)为y轴
- 3D图形学习中通常使用另一种坐标系, 即 正中心为原点,水平(右)为x轴,纵向(上)为y轴
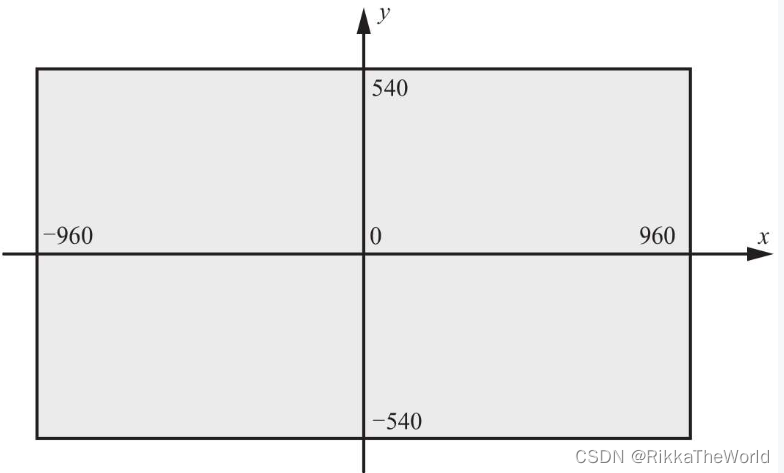
当前者坐标系转化到后者,需要进行简单的转化。
(Sx 、Sy为新坐标, Cx、Sy为旧坐标、Cw、Ch为范围宽高)
Sx = Cw/2 + Cx
Sy = Ch/2 - Cy
2 减色法模型
- 白光包含各种波长的光,当光照射到一个物体的表面时,物体的表面会吸收其一部分的光,反射其它部分的光,这取决于物体的材质。一些反射光会进入我们的眼睛,然后我们的大脑将其转化成颜色,这个颜色就是物体表面反射的波长总和所形成的颜色。
- 在白纸上用蜡笔画黄色,能看到黄色的原理:
- 因为是白纸,它能反射基本上所有的光
- 黄色的蜡笔在纸上画,其实是涂上了一层材料,这个材料可以吸收一部分波长的光,而其它波长的光则会通过
- 这些通过的光会被白纸反射,第二次穿过材料,进入我们的眼睛,我们的大脑会把这种特定波长的光组合解释成“黄色”
- 综上所述,这一层“黄色”的材料的作用就是从原始的白光中减去一部分特定波长的光。
- 同样可以思考其它颜色,我们在黄色上叠加蓝色,相当于是一个特定波长组合减去另一个特定波长组合,得到新的波长组合被我们的大脑解释为“绿色”
- 减色法中的三原色是:品红色(magenta)、青色(cyan)、黄色(yello),再加上原色:纯黑(因为前三色综合并不是一个纯黑色),这也是
CMYK颜色模型
3. 加色法模型
- 屏幕和纸张是相反的,纸张本身不发光,而是反射部分光。而屏幕本身是黑色的,但它们会自身发光。
- 对于纸张,我们减去不想要波长的光,而屏幕上,我们从没有光开始,然后添加我们想要的波长的光。
- 为此屏幕需要不同的原色,大多数颜色都可以来自红色(R)、蓝色(B)和绿色(G),也就是 RGB颜色模型,也是加法模型。
4. 颜色深度和颜色表示法
- 大部分场景下,用8位二进制来表示一种原色(FF),称一种原色为颜色通道。一个像素由三个通道组成,就是24位二进制,总共 2^24(1670万)种不同的原色。这种格式被称为
R8G8B8/888格式,我们认为这种格式的颜色深度为24位。 - 由于我们眼睛对绿色的变化比对红色和蓝色更加敏感,所以还有其它格式,例如
R5G6B5/565的16位格式, 也节省了内存。 - 我们使用三个字节来表示一种颜色,每个字节保存从0到255的8位颜色通道的值。我们将颜色表示为 (R,G,B),如 (232,131,20)
5. 光线追踪基本
- 我们通过视口(viewprot,也称为投影平面)进行观察, 而视口的大小(Vw、Vh)和视口到相机的距离(d)决定了相机可以观察的角度,称为视野(Field of view,简称
FOV)。人类有将近 180° 的水平视野。为简单起见,我们设置Vw=Vh=d=1,这样使得相机视野大约为 53°,从而可以生成合理的图像。 - 画布上的坐标(Cx,Cy)和视口坐标(Vx,Vy,Vz)的转化方程:
Vx = Cx Vw/CwVy = Cy Vh/ChVz = D
方程解读:我们在画布上画的就是视口上看到的东西,如果画布长宽大小等于视口长宽,则 (Cx, Cy) 和 (Vx, Vy) 是一样的,而大部分时候画布长宽和视口长宽不一样,但是比例一样,因此Cw/Cx = Vw/Vx;其次,摄像机到视口的距离就是到画布距离,因此 Vz 恒等为 d(可能后期摄像机会改变),所以得到这个方程。
- 射线方程:
P = O + t(V- O), O为相机点, V为射线上任意一点, P为O到V的线段距离,t为任意实数- 由于
V-O = D,因此方程亏简化为:P = O + tD
- 使用画布来光线追踪渲染球体模型,整体思路和步骤如下:
- 假设摄像机为原点,即
O(0,0,0), 球体为一个数据结构,能够知道它任意一点的颜色(Color)、圆心(CO)和半径® - 遍历画布,拿到任意像素点
C(Cx, Cy) - 根据画布-视口坐标转化方程,拿到其在视口中的坐标
V(Vx, Vy, Vz) - 获取射线 OV(O -> V)的射线方程(
P=O+tD), 并和球形上点方程((P-C)·(P-C)=r²)进行相交点计算, 根据二元一次方程,得出{t1, t2},要求 t 大于1且小于最大值(因为要画出视口前方的东西,所以视口之后的不需要展示), t 没有时(b²-4ac<0)说明没有射线和球没有相交。 t有一个值时(b²-4ac=0)说明相交于一点, t有两个值时(b²-4ac>0),此时要取离相机最近的那个值,也就是在范围中更小的那个 t值,因为远的那个我们在视口上看不到 - 通过 t 获取球上的一点,拿到其颜色(Color)
- 在画布
C(x,y)上绘制这个颜色
- 假设摄像机为原点,即
6. 光源
- 点光,在 3D 控件中的一个固定的点发射出光,这个点被称为点光源的位置,它向每个方向都均匀发射光,所以也被称为全向光(omnidirectional light),因此点光可以完全用位置和强度来进行描述。每个观察点 P 都距离光源 O 有不同的向量 L。
- 方向光,它有强度,但没有位置,它有一个固定的方向,类似人类与太阳(太过遥远,每条光都是平行线一样)。对于每个观察点 P,都距离光源 O 有相同的向量 L,L将会是 (太阳中心) - (地球中心)
- 环境光,3D环境中,光靠点光和方向光不足以照亮一个场景,因为这样要么全亮,要么全黑。现实世界中,当光照到一个物体时,它会吸收一部分光,并散射一部分光,这样我们才能看到阴影下的物体,所以一个物体被光照到时,它也便成为一个光源,但是这种模型是极其复杂的(全局光照(global illumination))。所以在 3D 环境中,我们声明环境光为场景中的每个点都贡献一点光,它只有强度这个象征(亮不亮暗不暗),这是一种粗略的简化,但是它的效果还可以。
一般来说,一个场景会有单个环境光(因为环境光只有一个强度,任意数量的环境光都可以简单地组合成一个环境光),和任意数量的点光和方向光。
-
向量点积(内积)
向量V和W的夹角为α,则它们的点积为:V · W = |V| · |W| · cos(α)
自身的点积为:V·V = Vx² + Vy² + Vz² = |V|²,也就是自身长度的平方 -
向量叉积
R = V × W,则计算过程如下:Rx = VyWz - VzWyRy = VzWx - VxWzRz = VxWy - VyWx
-
对漫反射建模(哑光物体)
若宽度(强度)为 I 的 L 向量光以β角度射到点 P,产生 A 区域,P点法向量为 N,那么:I/A = N·L/|N||L|, 这是反射光的比例函数,是物体表面法线和光线方向之间夹角的比例。它的取值范围是cos(90-β)=cos(α),由于大于 90 °时,该值是负数,因此相当于光找事到了其背面,相当于是黑暗的,因此我们只取其为正数的时候,也就是-90° <= α <= 90 °,0<=cos(α)<=1。
因此可以得出场景中点 P 的漫反射方程为:Ip = Ia + Σ(i=1 n)Ia(N·Li / |N||Li|),其中 Ia 为环境光强度, Li 为第i个方向光/点光的强度,西格玛用于计算每个点光或方向光的下单位面积的光强度,并去除N·Li < 0的情况 -
法向量 N 是单位向量,因此长度为1, 在球体中,若 C 为原点,则 P 点的法向量计算为:
N = P-C/|P-C| -
镜面反射(闪亮物体)
通过镜面反射,需要计算进入相机的反射光,因此还要加上这部分的轻度光。而用 S 来表示物体的光泽度,向量 R 表示光线根据法线反射出的向量。 V 向量(进入相机的向量)就是追踪光的 -D 向量。因此最终的反射方程为:
Ip = Ia + Σ(i=1,n)Ii [ (N·Li)/(|N||Li|) + (Ri·V)/|Ri||V|)² ],