数据结构–栈(Stack)的基本概念

线性表是具有相同数据类型的n (
n
≥
0
n\ge0
n≥0)个数据元素的有限序列,其中n为表长,当n = 0时线性表是一个空表。若用L命名线性表,则其一般表示为:
L
=
(
a
1
,
a
2
.
.
.
,
a
i
,
a
i
+
1
,
.
.
.
,
a
n
)
L = (a_1,a_2 ...,a_i, a_{i+1},...,a_n)
L=(a1,a2...,ai,ai+1,...,an)
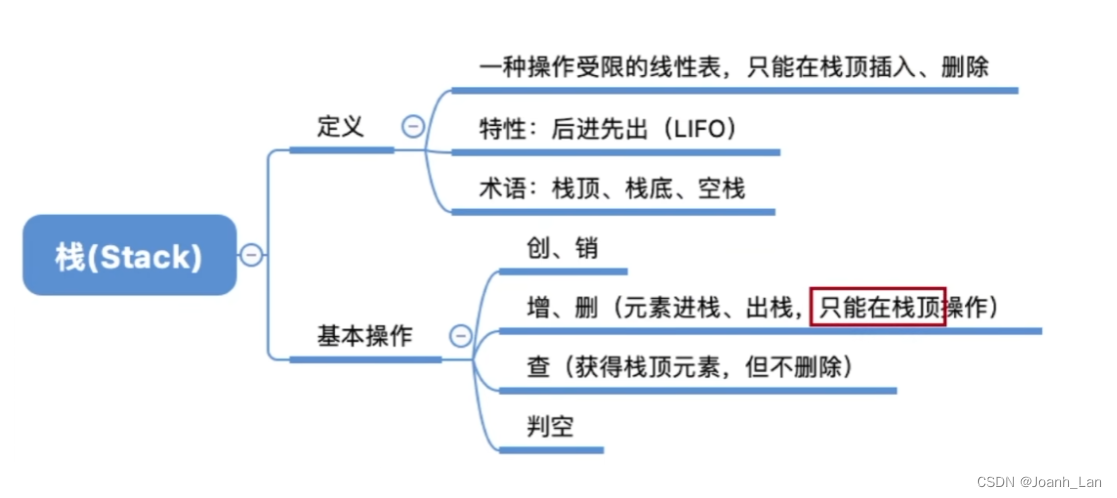
栈(Stack)是只允许在一端进行插入或删除操作的线性表

栈的定义
栈(Stack)是 只允许在一端进行插入或删除操作 \color{green}只允许在一端进行插入或删除操作 只允许在一端进行插入或删除操作的线性表
重要术语:栈顶、栈底、空栈


线性表的基本操作
创 & 销:
InitStack(&S):初始化栈。构造一个空栈s,分配内存空间。
DestroyStack(&S):销毁栈。销毁并释放栈s所占用的内存空间。
增 & 删:
Push(&S,x):进栈,若栈S未满,则将x加入使之成为新栈顶。
Pop(&S,&x):出栈,若栈s非空,则弹出栈顶元素,并用x返回。
查找:
GetTop(S,&x):读栈顶元素。若栈s非空,则用x返回栈顶元素
其他常用操作:
StackEmpty(S):判断一个栈s是否为空。若s为空,则返回true,否则返回false。
栈的常考题型
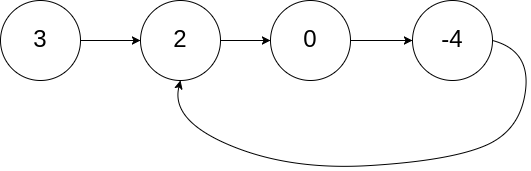
进栈顺序:
a
→
b
→
c
→
d
→
e
a \to b \to c \to d \to e
a→b→c→d→e
有哪些合法的出栈顺序?
n个不同元素进栈,出栈元素不同排列的个数为 1 n + 1 C 2 n n \frac{1}{n+1}C_{2n}^n n+11C2nn。上述公式称为卡特兰(catalan)数,可采用数学归纳法证明(不要求掌握)。
上题答案:
1
5
+
1
C
10
5
=
42
\frac{1}{5+1}C_{10}^5 = 42
5+11C105=42
知识点回顾与重要考点