目录
凸函数
凸函数定义
凸函数的判定
性质特点
拉格朗日乘子法
基本思想
有约束最优化问题
拉格朗日乘子法
凸函数
凸函数(Convex Function)是定义在凸集上的实值函数,具有以下性质:对于任意两个定义域内的点,函数上的连线段上的点的函数值不超过这两个点的函数值。
形式化地,设函数 f(x) 在凸集 C 上定义,对于 C 中的任意两个点 x1 和 x2,以及任意实数 t(0 <= t <= 1),满足以下不等式:
f(tx1 + (1-t)x2) <= tf(x1) + (1-t)f(x2)
其中,tx1 + (1-t)x2 是 x1 和 x2 的凸组合。
凸函数的几何直观解释是:函数上的每个点都位于连接该点的任意两个点所在的线段或曲线的上方。

凸函数定义
设函数f定义在凸集D上,若对于∀x,y∈D及 0≤θ≤1,都有f(θx+(1-θ)y)<θf(x)+(1-
θ)f(y),则称f为凸函数。
从图形上看,就是:凸函数在函数上任意找两点它们的连线(也就是割线)上的值比对
应的函数的值要大。
凸函数的判定
以一元函数为例,若函数f(x)有f''(x)>0,则函数f(x)就是凸函数。
例如:函数f(x)=x^2^,对应的二阶导是f''(x)=2,大于0,则f(x)=x^2^是一个凸函数
性质特点
- 局部最小值即为全局最小值:对于凸函数,任意局部极小值都是全局最小值,这意味着凸函数的优化问题不存在多个不同的局部最优解。
- 凸组合:凸函数对凸组合具有保持性质,即对于任意凸组合的点集,函数值的凸组合不超过对应点的凸组合。
- 一阶导数非递减:凸函数的一阶导数是非递减的,即随着自变量的增加,函数的斜率不会减小。
- 二阶导数非负:凸函数的二阶导数是非负的,即函数的曲率不会向下弯曲。
拉格朗日乘子法
拉格朗日乘子法(Lagrange Multiplier Method)是一种用于求解约束条件下的优化问题的方法。它通过引入拉格朗日乘子(Lagrange multipliers)将含有约束条件的优化问题转化为无约束条件的优化问题,从而求解原始问题的最优解。
考虑一个优化问题,目标是最小化(或最大化)目标函数 f(x)(或最大化),同时满足一些约束条件 g_i(x) ≤ 0 和 h_j(x) = 0,其中 g_i(x) 和 h_j(x) 是关于优化变量 x 的函数。

基本思想
拉格朗日乘子法主要用于解决有约束优化的问题,它的基本思想就是引入一组称为拉格朗日乘子的变量 λ_i 和 μ_j,构建一个新的函数,称为拉格朗日函数(Lagrange function):
L(x, λ, μ) = f(x) + Σλ_i * g_i(x) + Σμ_j * h_j(x)
其中,λ_i 和 μ_j 是拉格朗日乘子,用来对应约束条件。
然后,通过对拉格朗日函数求导,并令导数等于零,可以得到一组等式和不等式,称为拉格朗日乘子法的KKT条件(Karush-Kuhn-Tucker conditions)
KKT条件包括:
- 梯度条件:∇f(x) + Σλ_i * ∇g_i(x) + Σμ_j * ∇h_j(x) = 0
- 原始可行性条件:g_i(x) ≤ 0,h_j(x) = 0
- 对偶互补松弛条件:λ_i ≥ 0,λ_i * g_i(x) = 0
有约束最优化问题
将2l长的铁丝折成一个长为x,宽为y的长方形,如何折才能使得面积最大
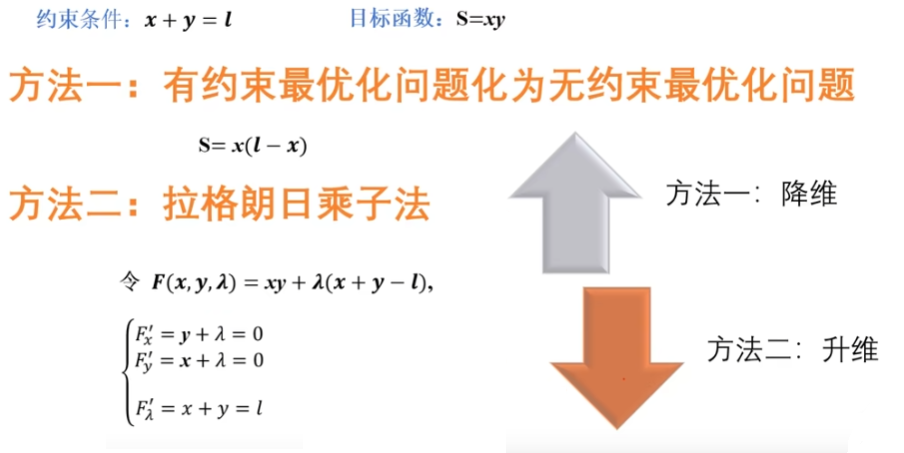
拉格朗日乘子法