数据分析知识图谱

在做数据分析时，经常会有这样的困扰：面对几种相似的方法，既不清楚它们各自的使用场景，也无法分清它们之间的差别，一念之差就可能选错方法。如果你也有这样的困扰，建议按照SPSSAU知识图谱目录顺序检索对应的研究方法，理清不同方法的区别与使用场景，以便选出正确的方法进行分析。SPSSAU知识目录如下：

1、基本描述统计

基本描述统计分析包括频数分析、描述分析、分类汇总；用于对收集的数据进行基本的说明。

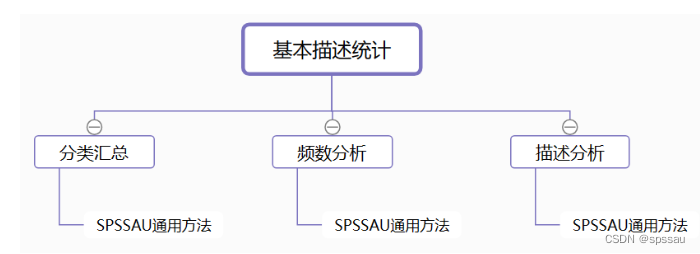
频数分析：用于分析定类数据的选择频数和百分比分布。
描述分析：用于分析定量数据的集中趋势、波动情况和分布状况等；常见的指标有平均值、中位数、标准差等；更深入的描述指标包括百分位数、峰度、偏度、变异系数等。
分类汇总：用于交叉研究，展示两个或者更多变量的交叉信息，可以将不同组别下的数据进行汇总统计。

下方链接均会跳转至SPSSAU帮助手册：

频数分析

描述分析

分类汇总

2、信度分析

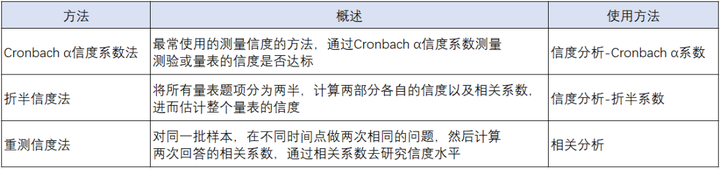
信度分析的方法主要有以下三种：Cronbach α信度系数法、折半信度法、重测信度法。

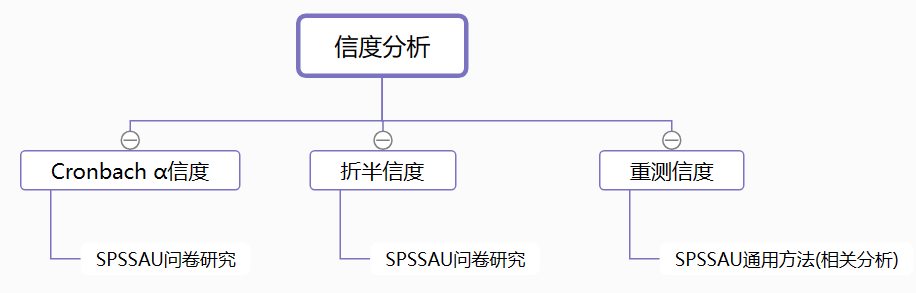
Cronbach α信度：最常使用的方法，通过Cronbach α信度系数测量测验或量表的信度是否达标。
折半信度：是将所有量表题项分为两半，计算两部分各自的信度以及相关系数，进而估计整个量表的信度的测量方法。
重测信度：是指同一批样本，在不同时间点做了两次相同的问题，然后计算两次回答的相关系数，通过相关系数去研究信度水平。

下方链接均会跳转至SPSSAU帮助手册：

Cronbach α信度

折半信度法

重测信度（使用相关系数分析）

3、效度分析

效度有很多种，可分为四种类型：内容效度、结构效度、区分效度、聚合效度。

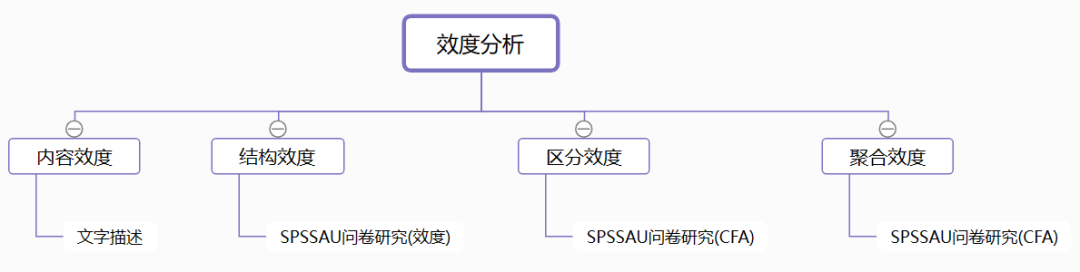
内容效度：用文字描述量表的有效性，比如具有参考文献来源，量表经过专家认可等。
结构效度：因子与测量项对应关系是否符合预期，如果符合预期则说明具有结构效度。
区分效度：强调本不应该在同一因子下的测量项，确实不在同一因子下面。
聚合效度：强调本应该在同一因子下面的测量项，确实在同一因子下面。

下方链接均会跳转至SPSSAU帮助手册：

结构效度

区分效度&聚合效度

4、差异关系研究

常见的差异关系研究方法包括方差分析、t检验、卡方检验、非参数检验。

t 检验：X为定类数据，Y为定量数据之间的关系情况，且X只能为2个类别。
方差分析：X为定类数据，Y为定量数据，且组别多于2组时可使用方差分析。
交叉卡方：分析定类数据和定类数据之间的关系情况，可使用交叉卡方分析。
非参数检验：数据不正态或者方差不齐时，可使用非参数检验。

提示：t检验和方差分析均属于参数检验范围，一般需要数据满足正态性、方差齐性。与参数检验相对的是非参数检验，非参数检验不对总体的分布形态做假定，所以当数据不正态或方差不齐时，可使用非参数检验进行差异性研究。

下方链接均会跳转至SPSSAU帮助手册：

t检验
方差分析交叉卡方非参数检验

5、t检验

t检验，用于分析定类数据与定量数据之间的差异情况，按照研究内容和数据类型等不同，可分为以下几类：

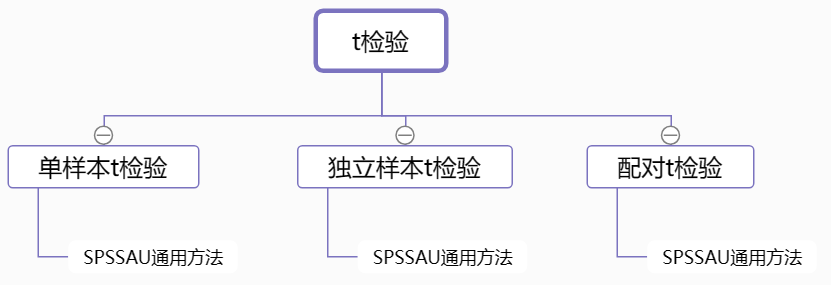
单样本t检验：对比一组定量数据与某个数字的差异。
独立样本t检验：对比X定类数据与Y定量数据之间的差异。
配对t检验：对比两组配对数据之间的差异。

下方链接均会跳转至SPSSAU帮助手册：

单样本t检验

独立样本t检验

配对t检验

6、方差分析

方差分析用于进行定类数据与定量数据之间的差异关系研究；按照研究内容和数据类型等不同，可分为以下几类：

单因素方差分析：如果X为一个，则使用单因素方差分析。
双因素方差分析：当X个数为2个，则使用双因素方差分析。
多因素方差分析：当X个数超过2个，使用多因素方差分析。
事后多重比较：是基于方差分析基础上进行，如果X的组别超过两组，可用事后多重比较进一步分析两两组别之间的差异。
协方差分析：如果研究中有干扰因素（控制变量），可使用协方差分析。
重复测量方差分析：相关领域（比如医学研究时）常常需要对同一观察单位重复进行多次测量，此时使用重复测量方差分析。

下方链接均会跳转至SPSSAU帮助手册：

单因素方差分析

双因素方差分析

多因素方差分析

事后多重比较

协方差分析

重复测量方差分析

7、卡方检验

卡方检验，用于分析定类数据与定类数据之间的差异情况，按照研究内容和数据类型等不同，可分为以下几类：

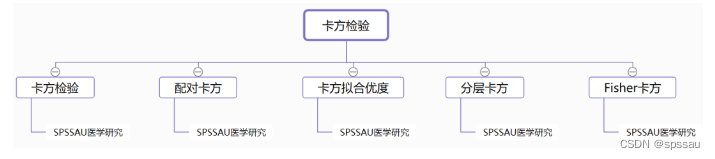
卡方检验：定类数据与定类数据之间的差异情况。
配对卡方：两组配对定类数据之间的差异情况。
卡方拟合优度：研究类别定类数据的实际比例与预期比例是否一致。
分层卡方：分层卡方是在卡方检验基础上，进一步考虑分层项的干扰。
Fisher卡方：在分析样本量较少（比如小于40），也或者期望频数出现小于5时，使用fisher卡方检验较为适合。

下方链接均会跳转至SPSSAU帮助手册：

卡方检验

配对卡方

卡方拟合优度

分层卡方

Fisher卡方

8、非参数检验

非参数检验用于研究定类数据与定量数据之间的关系情况。如果数据不满足正态性或方差不齐，可用非参数检验。

单样本Wilcoxon检验：是当数据不服从正态分布时，可检验数据是否与某数字是否有明显的区别。
MannWhitney：对于不服从正态分布的变量进行差异性分析，如果X的组别为两组，则使用MannWhitney统计量。
Kruskal-Wallis：如果组别超过两组，则应该使用Kruskal-Wallis统计量。
配对样本Wilcoxon检验：如果是配对数据，则使用配对样本Wilcoxon检验。
多样本Friedman检验/Cochran's Q 检验：对于多个关联样本的差异情况。
Ridit分析：如果是研究定类数据与定量（等级）数据之间的差异性，还可以使用Ridit分析。

下方链接均会跳转至SPSSAU帮助手册：

单样本wilcoxon检验

MannWhitney、Kruskal-Wallis（非参数检验）
配对样本Wilcoxon检验

多样本Friedman检验/Cochran's Q 检验Ridit分析

9、相关分析研究

相关分析可分为简单相关分析、偏相关分析、典型相关分析三类。

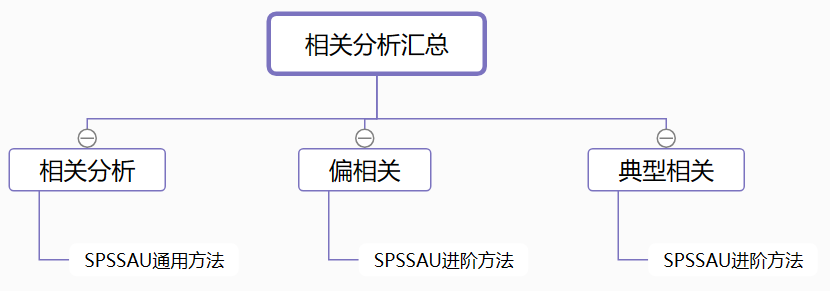
相关分析：简单相关分析是分析对两个变量之间的相关关系。
偏相关分析：当两个变量都与第三个变量相关时，为了消除第三个变量的影响，只关注这两个变量之间的关系情况，此时可使用偏相关分析。
典型相关分析：研究两组变量（多个指标组成）之间的整体相关性，可用典型相关分析。

下方链接均会跳转至SPSSAU帮助手册：

10、线性回归研究

Y为定量数据时，可以使用线性回归研究X对Y的影响。常用的线性回归方法有以下几种：

线性回归：研究X对Y（定量数据）的影响关系情况。
逐步回归：如果X很多时，可使用逐步回归自动找出有影响的X。
岭回归：用于解决线性回归中自变量共线性的研究算法。
分层回归：如果需要研究多个线性回归的层叠变化情况，此时可使用分层回归。
Robust回归：如果数据中有异常值，可使用Robust回归进行研究。

下方链接均会跳转至SPSSAU帮助手册：

线性回归

逐步回归

岭回归

分层回归

Robust回归

11、logistic回归研究

Y为定类数据时，可以使用logistic回归研究X对Y的影响。

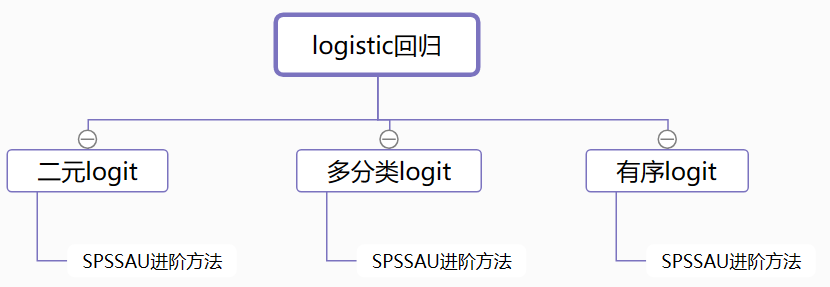
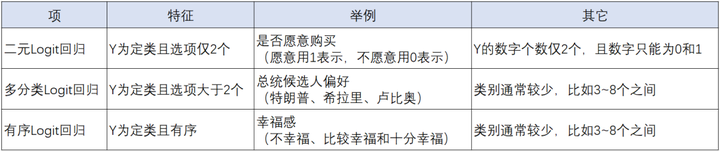
二元logit回归：Y为定类数据且只有两类
多分类logit：Y为定类数据且大于2类
有序logit：Y为定类数据且有序

下方链接均会跳转至SPSSAU帮助手册：

二元logit回归

有序logit回归

多分类logit回归

12、多选题研究

多选题分析可分为四种类型包括：多选题、单选-多选、多选-单选、多选-多选。

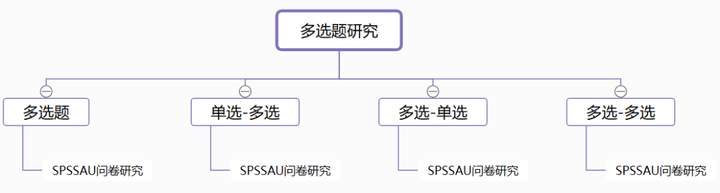
多选题分析：是针对单个多选题的分析方法，可分析多选题各项的选择比例情况。
单选-多选：是针对X为单选，Y为多选的情况使用的方。
多选-单选：是针对X为多选，Y为单选的情况使用的方法。
多选-多选：是针对X为多选，Y为多选的情况使用的方法。

下方链接均会跳转至SPSSAU帮助手册：

多选题分析
单选-多选多选-单选多选-多选

13、聚类分析方法

聚类分析以多个研究标题作为基准，对样本对象进行分类。

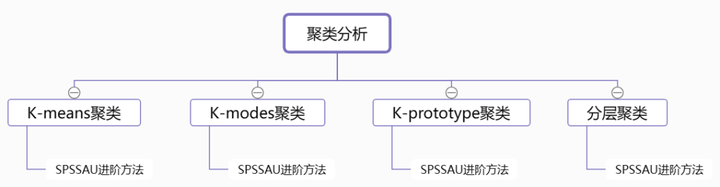
K-means聚类：只能处理数值型数据。
K-modes聚类：对分类属性数据进行聚类的方法。
K-prototype聚类：处理混合属性数据的方法。
分层聚类：对给定数据对象的集合进行层次分解，根据分层分解采用的分解策略，仅针对定量数据进行分层聚类。

下方链接均会跳转至SPSSAU帮助手册：

聚类分析（K-means、K-modes、K-prototype）

分层聚类

14、信息浓缩方法

当研究中包括有很多题目或很多变量时，可通过信息浓缩的方法，把数据浓缩成一个或多个变量，以便用于后续的分析。

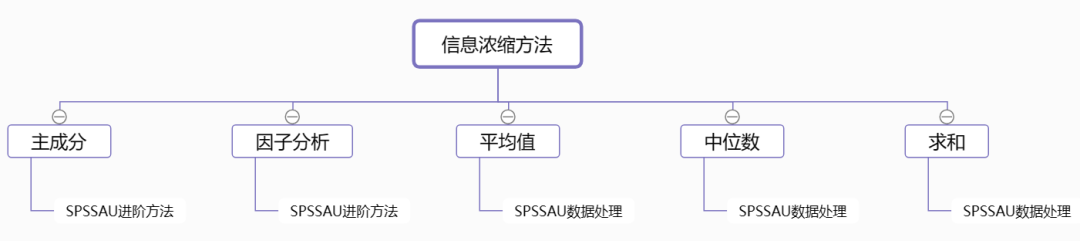
主成分分析和因子分析：都是信息浓缩的方法，即将多个分析项信息浓缩成几个概括性指标。如果希望进行将指标命名，SPSSAU建议使用因子分析。原因在于因子分析在主成分基础上，多出一项旋转功能，该旋转目的即在于命名。
平均值和求和：也是信息浓缩的常用方法，比如要将多个题项合并成一个变量，可通过求平均值概括成一个题项。
中位数：当数据不满足正态，存在极端值时，可用中位数代替平均值。

下方链接均会跳转至SPSSAU帮助手册：

因子分析

主成分分析

15、一致性研究方法

一致性检验的目的在于比较不同方法得到的结果是否具有一致性。检验一致性的方法有很多比如：Kappa检验、ICC组内相关系数、Kendall W协调系数等。

ICC组内相关系数：用于分析多次数据的一致性情况，分析定量或定类数据均可。
Kappa一致性检验：适用于两次方法之间比较一致性，通常要求数据为定类数据。
Kendall协调系数：分析多个数据之间关联性的方法，适用于定量数据，尤其是定序等级数据。

下方链接均会跳转至SPSSAU帮助手册：

Kappa一致性检验

Kendall协调系数

ICC组内相关系数

16、权重研究

权重研究是用于分析各因素或指标在综合体系中的重要程度，最终构建出权重体系。权重研究有多种方法：

AHP层次分析法：是一种主观加客观赋值的计算权重的方法。先通过专家打分构造判断矩阵，然后量化计算每个指标的权重。
熵值法：是利用熵值携带的信息计算每个指标的权重，通常可配合因子分析或主成分分析得到一级权重，利用熵值法计算二级权重。
TOPSIS法：是一种评价多个样本综合排名的方法，用于比较样本的排名情况。
因子分析：可将多个题项浓缩成几个概括性指标（因子），然后对新生成的各概括性指标计算权重。
主成分分析：利用方差解释率值计算各概括性指标的权重。
其他：熵权topsis法、优序图法、CRITIC权重、独立性权重、信息量权重等。

下方链接均会跳转至SPSSAU帮助手册：

AHP层次分析法

熵值法

TOPSIS法

因子分析

主成分分析

17、模型研究方法

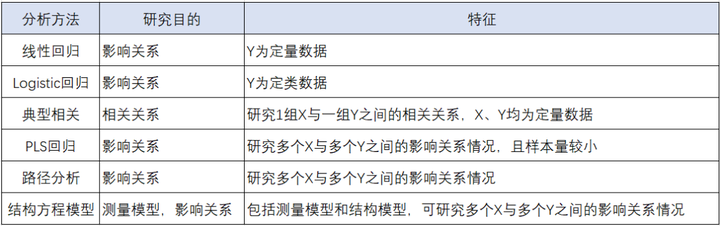
当需要研究多个变量之间的关系情况时，通常可构建统计模型用于分析及预测。

线性回归：当研究X对Y的影响关系，其中Y为定量数据，可使用线性回归分析。
logistic回归：研究X对Y的影响关系，其中Y为定类数据，可使用Logistic分析。
典型相关：研究1组X与一组Y之间的关系情况，可使用典型相关分析。
PLS回归：研究多个X与多个Y之间的影响关系情况，且样本量较小（通常小于200），可使用PLS回归分析。
路径分析：如需分析多个X对多个Y的影响关系，以及具体哪些X对哪些Y有影响、如何影响，可使用路径分析。
结构方程模型：需要同时研究测量关系和影响关系，可使用结构方程模型。

下方链接均会跳转至SPSSAU帮助手册：

线性回归

logistic回归

典型相关

PLS回归

路径分析

结构方程模型

18、数据分布研究

判断数据分布是选择正确分析方法的重要前提。

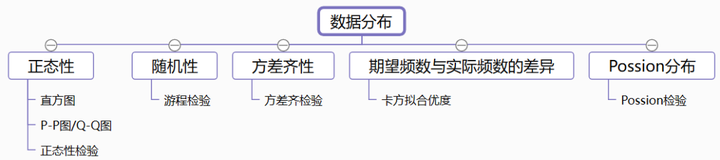
正态性：很多分析方法的使用前提都是要求数据服从正态性，比如线性回归分析、相关分析、方差分析等，可通过直方图、P-P/Q-Q图、正态性检验查看数据正态性。
随机性：抽样调查有一个最基本的前提假设，就是抽样必须满足“随机性要求”，游程检验是一种非参数性统计假设的检验方法，可用于分析数据是否为随机。
方差齐性：方差齐检验用于分析不同定类数据组别对定量数据时的波动情况是否一致，即方差齐性。方差齐是方差分析的前提，如果不满足则不能使用方差分析。
卡方拟合优度检验：卡方拟合优度检验是一种非参数检验方法，其用于研究实际比例情况，是否与预期比例表现一致，但只针对于类别数据。
Poisson分布：如果要判断数据是否满足Poisson分布，可通过Poisson检验判断或者通过特征进行判断是否基本符合Poisson分布（三个特征即：平稳性、独立性和普通性）

下方链接均会跳转至SPSSAU帮助手册：

正态性检验

游程检验

方差齐检验

卡方拟合优度

Possion检验