目录
- 1. 人脸识别是什么及应用场景
- 2. 人脸识别的组成
- 2.1 前端图像采集
- 2.2 后端智能平台
- 3.人脸技术的流程
- 3.1人脸检测
- 3.2人脸对齐
- 3.2.1仿射变换
- 3.2.2对齐方法
- 3.3人脸编码(提取特征向量)
- 3.4人脸分类
1. 人脸识别是什么及应用场景
人脸识别特指利用分析比较人脸视觉特征信息进行身份鉴别的计算机技术。人脸识别技术主要用于身份验证,常见的场景有小区、楼宇、校园、工厂、园区、银行等,如:智能门禁、人脸闸机、人脸考勤、智能门锁等。通过人脸识别验证身份,来保障相关场所的安全,也减少了人工审核的成本。
在安防监控中,人脸识别也意义重大,比如公众场所(地铁站、车站、街道、酒店等)的安防布控、公安部追捕嫌疑犯等。基于公众场所的安防监控摄像头,通过抓拍人脸并将结果上传公安部网络,与嫌疑犯人脸进行比对,协助公安人员的执法工作。
人脸识别技术是人工智能领域的关键技术,在智能视频监控系统具有十分广泛的应用前景。
2. 人脸识别的组成
2.1 前端图像采集
前端人脸图像采集系统通过抓拍采集人脸图像、实时视频流等,如视频监控摄像头、智能考勤机、智能门禁机等设备,都具备人脸采集抓拍的功能。
2.2 后端智能平台
后端的智能平台可将前端采集的相关数据统一进行汇聚、处理、存储、应用、管理与共享,并结合人脸识别系统,实现人脸识别功能,并应用在现实场景中如:人脸识别考勤、人脸门禁、公安部的人脸追踪、抓捕嫌疑犯等等。
3.人脸技术的流程
3.1人脸检测
人脸检测在实际中主要用于人脸识别的预处理,即在图像中准确标定出人脸的位置和大小。
从照片中找出人脸的位置,以图片左上角为坐标原点,分别记录下人脸框左上角和右下角的坐标,并将人脸部分裁剪出来。
3.2人脸对齐
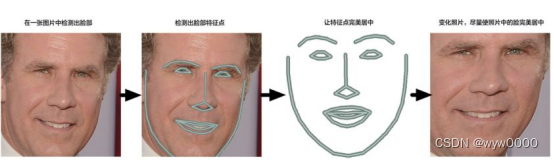
在现实场景中,往往前端设备抓拍获得的人脸不一定是正脸的角度,所以需要将图像中的人脸姿态进行矫正。通过人脸关键点检测得到人脸的关键点坐标,根据人脸的关键点坐标调整人脸的角度,使人脸对齐。如图,这两个脸在计算机看来,是完全不同的两张脸,因此我们需要通过一些仿射变换将脸部进行对齐。
人脸对齐可以极大的提高人脸识别的精度,因为人脸的关键点可以使要识别的人脸做一个空间归一化,这个空间归一化的操作就叫人脸对齐,这个操作可以使后续提取到与五官的位置无关,只有五官的形状纹理相关的特征。
人脸对齐是通过将人脸上的眼睛,鼻子,嘴巴对准到一个预设的固定位置上。
3.2.1仿射变换
仿射变换的功能是从二维坐标到二维坐标之间的线性变换,且保持二维图形的“平直性”和“平行性”(直线之间的相对位置关系保持不变,平行线经仿射变换后依然为平行线,且直线上点的位置顺序不会发生变化)
3.2.2对齐方法
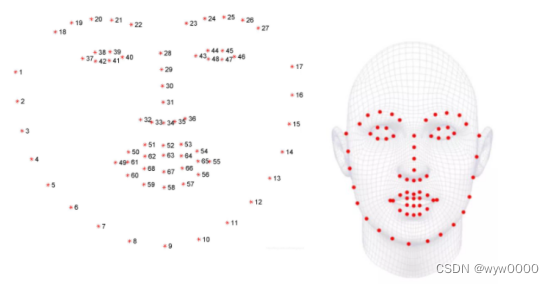
使用训练好的模型,自动地从检测出的人脸中标记出68个特征点(landmarks),然后在模板库中寻找一个标准模板,使用仿射变化,将这个68个点与模板的68个点对齐。
68个关键点
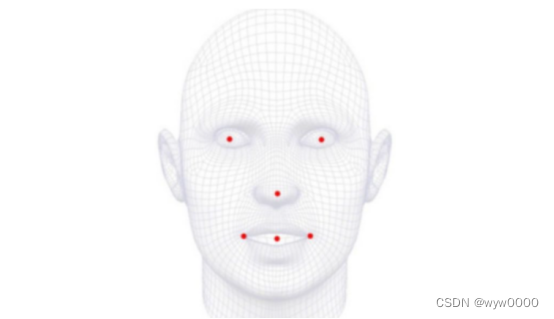
6个关键点
还有81、106个,旷世声称做到提取1000个关键点。
3.3人脸编码(提取特征向量)
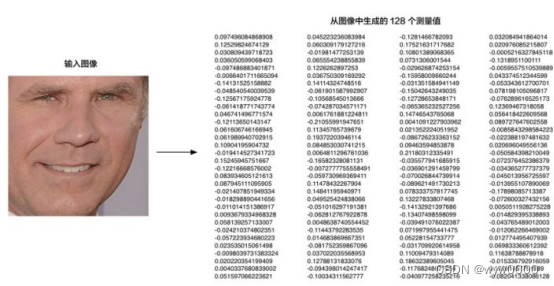
通过卷积神经网络训练一个模型,将送入的模型脸部图片自动编码成一个具有一个很强语义的128维向量。
3.4人脸分类
依次计算输入图像和数据库中每个图片的128位向量差值的欧氏距离,直到找到小于我们阈值的那张,到此,人脸识别成功。