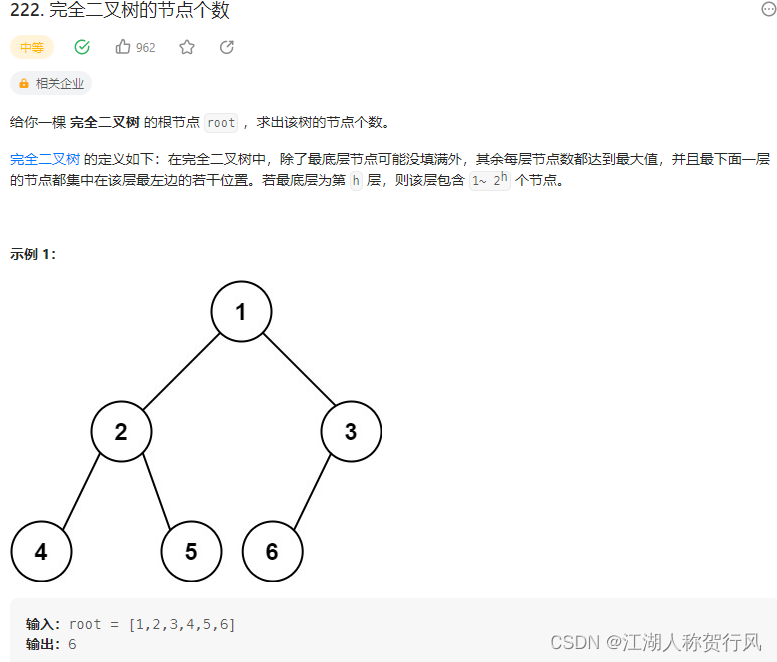
题目来源：https://leetcode.cn/problems/count-complete-tree-nodes/description/

 

 C++题解1：层序遍历计算节点。

• 时间复杂度：O(n)
• 空间复杂度：O(n)

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        int res = 0;
        if(root != nullptr) que.push(root);
        while(!que.empty()) {
            int len = que.size();
            for(int i = 0; i < len; i++) {
                TreeNode* cur = que.front();
                que.pop();
                if(cur->left != nullptr) que.push(cur->left);
                if(cur->right != nullptr) que.push(cur->right);
                res++;
            }
        }
        return res;
    }
};

C++题解2：完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

• 时间复杂度：O(log n × log n)  本质上是要看: 递归的次数 * 每次递归中的操作次数
• 空间复杂度：O(log n)

class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == nullptr) return 0;
        TreeNode* leftnode = root->left;
        TreeNode* rightnode = root->right;
        int depleft = 0, depright = 0;
        while(leftnode != nullptr){
            depleft++;
            leftnode = leftnode->left;
        }
        while(rightnode != nullptr) {
            depright++;
            rightnode = rightnode->right;
        }
        if(depleft == depright) return pow(2, depleft+1)- 1;
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};