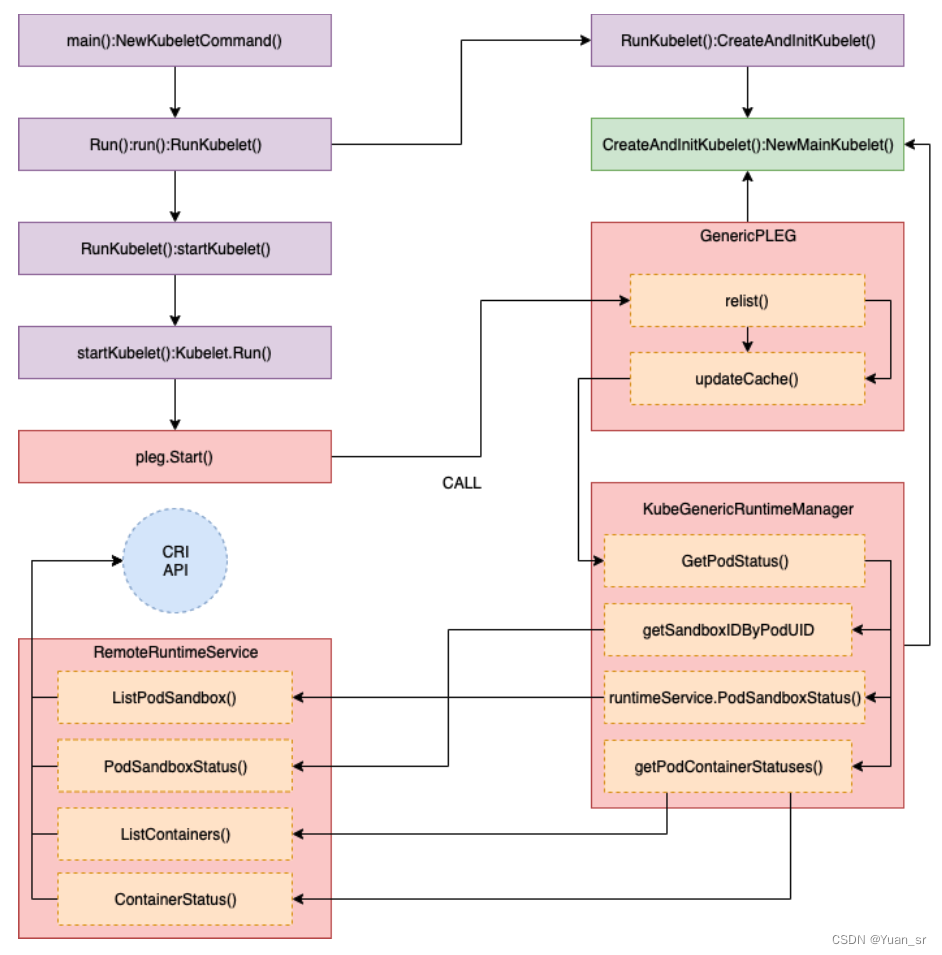
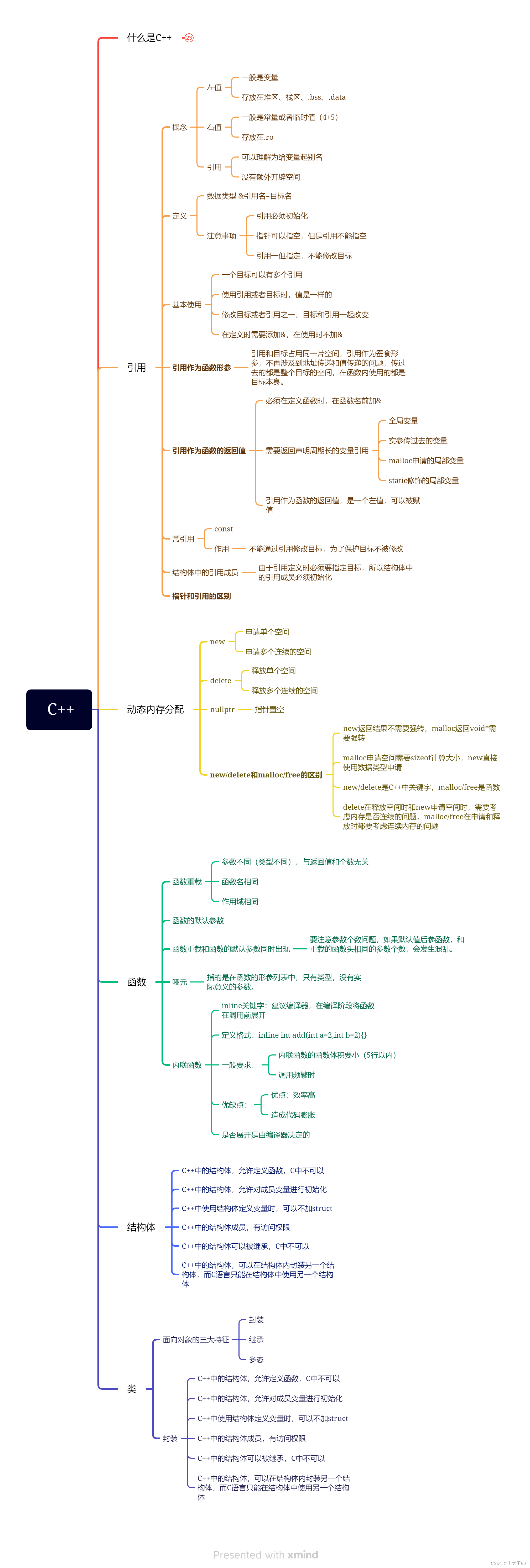
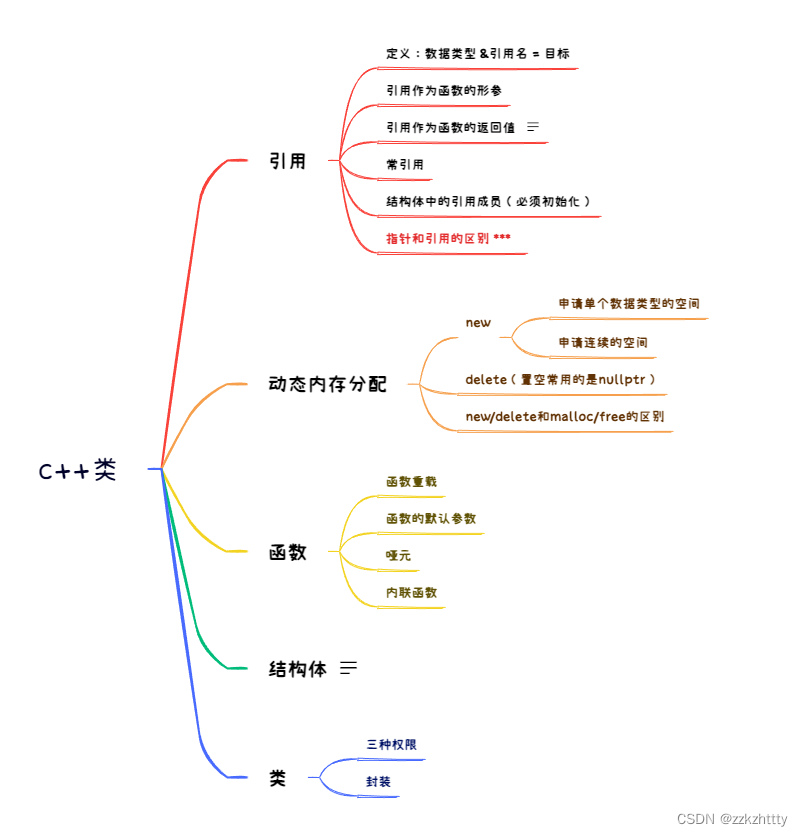
介绍下处理深度学习的框架DeZero,通过这个框架来了解自动微分是如何实现的
自动微分指的是自动求出导数的做法(技术)。“自动求出导数”是指由计算机(而非人)求出导数。具体来说,它是指在对某个计算(函数)编码后计算机会自动求出该计算的导数的系统。
自动微分。这是一种采用链式法则求导的方法。我们对某个函数编码后,可以通过自动微分高效地求出高精度的导数。反向传播也是自动微分的一种。反向传播相当于反向模式的自动微分。
自动微分是用计算机求导的一种方法。深度学习框架中实的是反向模式的自动微分。
实现Variable类
在DeZero中,变量都是通过Variable类来实现的,也就是让Variable类具有箱子的作用,看下面Variable的实现
class Variable:
def __init__(self, data):
self.data = data
实现Function类
Function类的实现如下:
class Function:
# __call__ 重写调用方法
def __call__(self, input):
x = input.data # 取出数据
y = self.forward(x) # 具体计算在forward中进行
output = Variable(y) # 作为Variable返回
return output
def forward(self, x):
# 暂时不实现
raise NotImplementedError()
在DeZero框架中,将Function类作为基类,实现所有函数通用的功能;具体函数时在继承了Function类的类中实现
在具体的使用中,继承自Function类并对输入值进行平方的类。这个类的名字是Square,代码如下所示:
class Square(Function):
def forward(self, x):
return x ** 2
具体实现如下:
x = Variable(np.array(10))
f = Square()
y = f(x)
print(type(y) # <class '__main__.Variable'>
print(y.data) # 100
手动进行反向传播
下面实现支持反向传播的Variable类。为此,要扩展Variable类,除普通值(data)之外,增加与之对应的导数值(grad)。
class Variable:
def __init__(self, data):
self.data = data
self.grad = None # 要在通过反向传播实际计算导数时将其设置为求出的值。
然后要扩展Function类
在当前的Function类上还要新增下面两个功能
- 计算导数的反向传播(backward)功能
- 调用forward方法时,保有被输入的Variable实例的功能
class Function:
# __call__ 重写调用方法
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
self.input = input # 保存输入的变量
return output
def forward(self, x):
# 暂时不实现
raise NotImplementedError()
def backward(self, gy):
# 暂时不实现
raise NotImplementedError()
看下面实际的例子
要实现具体函数的反向传播,首先看之前实现的Square类
class Square(Function):
def forward(self, x):
y = x ** 2
return y
def backward(self, gy):
x = self.input.data
gx = 2 * x * gy
return gx
接下来看Exp类, y = ex ,这个类可以按下面的方式实现
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return y
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx
反向传播的例子
首先看正向传播的代码
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
再通过反向传播计算y的导数
y.grad = np.array(1.0)
b.grad = C.backward(y.grad)
a.grad = B.backward(b.grad)
x.grad = A.backward(a.grad)
print(x.grad)
反向传播的自动化
下面就要让反向传播自动化,也就是要建立这样的机制:无论普通的计算流程(正向传播)中是什么样的计算,反向传播都可以自动进行。
之前做的流水线式的计算,只要以列表的形式记录函数的顺序,就可以通过反向回溯自动进行反向传播。不过,对于有分支的计算图或多次使用同一个变量的复杂计算图,只借助简单的列表就不能奏效了。接下来的目标是建立一个不管计算图多么复杂,都能自动进行反向传播的机制。
其实只要在列表的数据结构上想想办法,将所做的计算添加到列表中,或许可以对任意的计算图准确地进行反向传播。
要实现自动化就要在函数和变量之间建立联系,要让这个“连接”在执行普通计算(正向传播)的那一刻创建,因此要在Variable类中添加以下代码:
class Variable:
def __init__(self,data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
在Function中添加代码
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
output.set_creator(self) # 让输出变量保存创造者信息
self.input = input
self.output = output # 也保存输出变量
return output
变量和函数连接的这个特征就是Define-by-Run。换言之是通过数据的流转建立起来的。这种带有“连接”的数据结构叫作连接节点。
下面利用变量和函数之间的连接,尝试实现反向传播。
下面实现从变量y到b的反向传播
y.grad = np.array(1.0)
C = y.creator # 获取函数
b = C.input # 获取函数的输入
b.grad = C.backward(y.grad) # 调用函数的backward方法
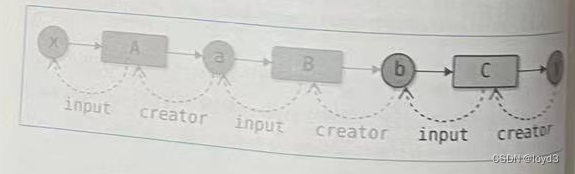
下面实现从变量b到变量a反向传播
B = b.creator # 获取函数
a = B.input # 获取函数的输入
a.grad = B.backward(b.grad) # 调用函数的backward方法
具体来说
流程如下:
- 获取函数
- 获取函数的输入
- 调用函数的backward方法
为Variable增加backward方法
从前面这些反向传播的代码可以看出。它们有着相同的处理方式。为了自动完成这些重复的处理。可以在Variable类中添加一个新的方法 —— backward
class Variable:
def __init__(self,data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
f = self.creator # 1. Get a function
if f is not None:
x = f.input # 2. Get the function's input
# 递归调用
x.grad = f.backward(self.grad) # 3. Call the function's backward
x.backward()
上面使用这个新的Variable自动进行反向传播
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
# backward
y.grad = np.array(1.0)
y.backward()
print(x.grad) # 输出结果 3.297442541400256
循环实现
在之前Variable的实现中
backward方法内调用backward方法,被调用backward方法内再次调用backward方法的处理会不断延续下去直到某个self.creator函数为None的Variable变量,所以这是个递归结构
下面要使用循环实现,代码如下:
class Variable:
def __init__(self,data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
# 按顺序向funcs列表里添加应该处理的函数。
funcs = [self.creator]
while funcs:
f = funcs.pop() # 获取函数 列表的pop方法会删除列表末尾的元素,并取出这个元素的值。
x, y = f.input, f.output # 获取函数的输入
x.grad = f.backward(y.grad) # backward调用backward方法
if x.creator is not None:
funcs.append(x.creator) # 将前一个函数添加到列表中
之所以要把递归变成循环,主要是为了处理复杂的计算图,使用循环代码实现很容易扩展到复杂的计算图处理,而且执行效率会变高