1、题目

第一年农场有 1 只成熟的母牛 A，往后的每年：

1）每一只成熟的母牛都会生一只母牛

2）每一只新出生的母牛都在出生的第三年成熟

3）每一只母牛永远不会死

2、思路

举例说明：

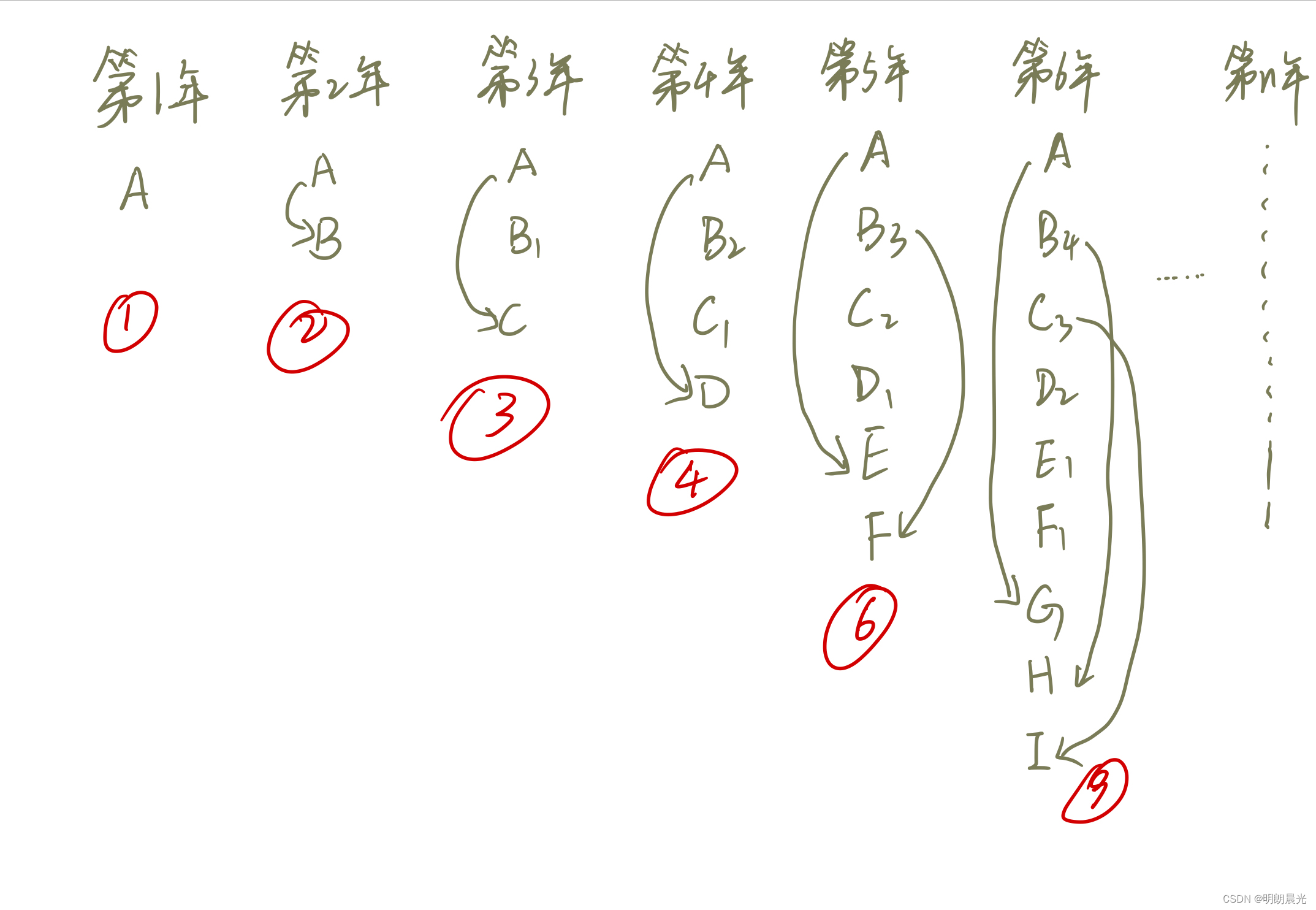
可得到递推式为：$F(n)=F(n-1)+F(n-3)$，含义为第 $n$ 年的牛 = 去年牛的数量 + 三年前牛的数量，因为三年前的牛会生牛。该式子是严格递推式，3 阶问题，有 $O(logn)$ 的解法。

根据矩阵乘法规则：

而仅凭这一个式子是无法推导出 3 阶矩阵的，于是往后多推导几项：

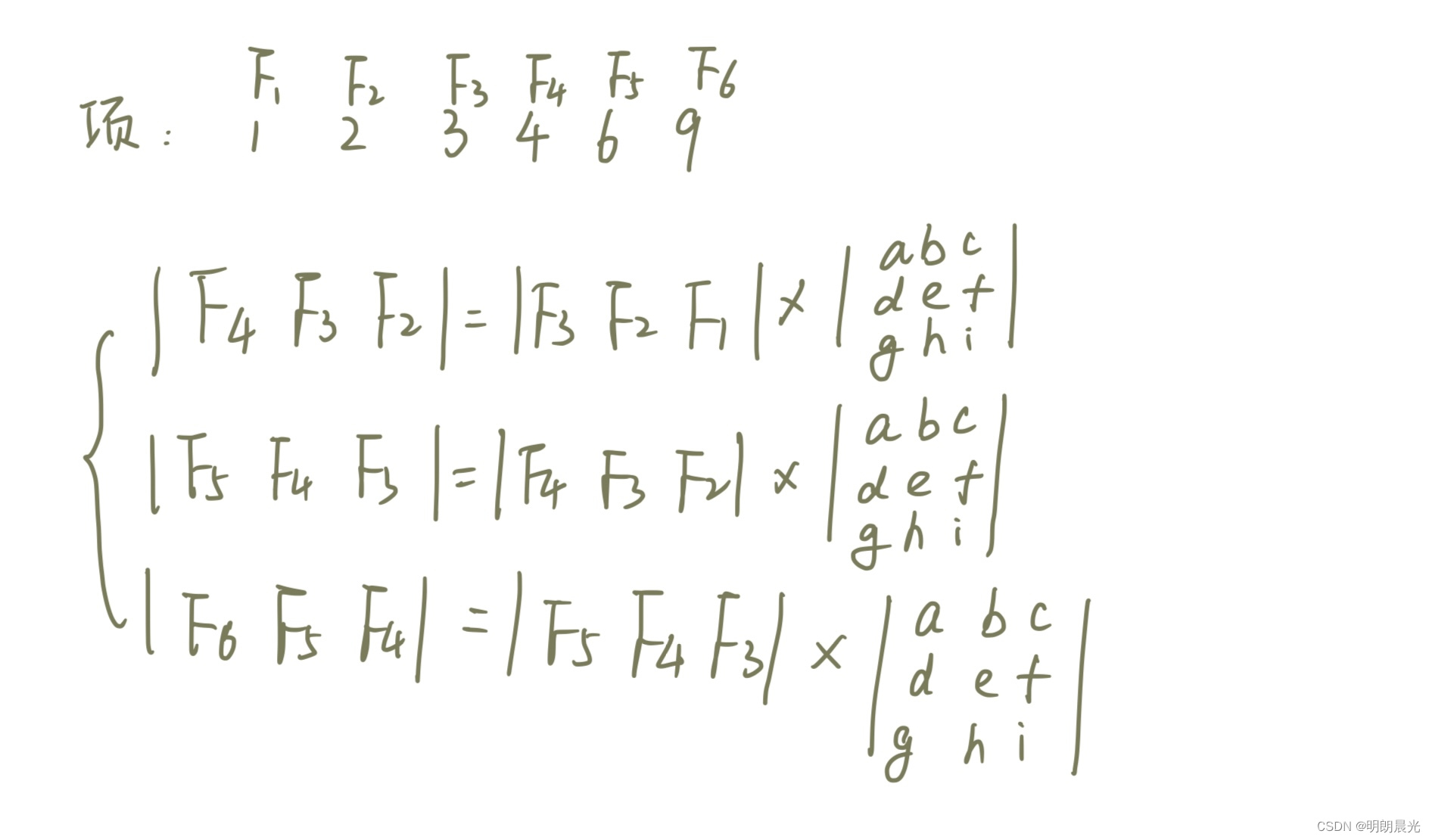
得到：

于是，代码实现：

public class Cow {
    //暴力递归
	public static int c1(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1 || n == 2 || n == 3) {
			return n;
		}
		return c1(n - 1) + c1(n - 3);
	}

    //递推，O(n)
	public static int c2(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1 || n == 2 || n == 3) {
			return n;
		}
		int res = 3;
		int pre = 2;
		int prepre = 1;
		int tmp1 = 0;
		int tmp2 = 0;
		for (int i = 4; i <= n; i++) {
			tmp1 = res;
			tmp2 = pre;
			res = res + prepre;
			pre = tmp1;
			prepre = tmp2;
		}
		return res;
	}

    //(logn)
	public static int c3(int n) {
		if (n < 1) {
			return 0;
		}
		if (n == 1 || n == 2 || n == 3) {
			return n;
		}
		int[][] base = { 
				{ 1, 1, 0 }, 
				{ 0, 0, 1 }, 
				{ 1, 0, 0 } };
		int[][] res = matrixPower(base, n - 3);
		return 3 * res[0][0] + 2 * res[1][0] + res[2][0];
	}
    
    public static int[][] matrixPower(int[][] m, int p) {
		int[][] res = new int[m.length][m[0].length];
		for (int i = 0; i < res.length; i++) {
			res[i][i] = 1; //对角线为1
		}
		// res = 矩阵中的1
		int[][] t = m;// 矩阵1次方
		for (; p != 0; p >>= 1) { //右移
			if ((p & 1) != 0) { //p&1得到次方的二进制形式最后1位，如果为1表示当前的值需要
				res = product(res, t);
			}
			t = product(t, t);
		}
		return res;
	}

	// 两个矩阵乘完之后的结果返回
	public static int[][] product(int[][] a, int[][] b) {
		int n = a.length;
		int m = b[0].length;
		int k = a[0].length; // a的列数同时也是b的行数
		int[][] ans = new int[n][m];
		for(int i = 0 ; i < n; i++) {
			for(int j = 0 ; j < m;j++) {
				for(int c = 0; c < k; c++) {
					ans[i][j] += a[i][c] * b[c][j];
				}
			}
		}
		return ans;
	}  

	public static void main(String[] args) {
		int n = 19;
		System.out.println(c1(n));
		System.out.println(c2(n));
		System.out.println(c3(n));
		System.out.println("===");

	}
}

如果牛在 5 年后会死，那么递推式为：$F(n)=F(n-1)+F(n-3)-F(n-5)$，就是一个 5 阶矩阵的问题。