作者主页：爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?type=blog个人简介：打工人。

持续分享：机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。

如发现文章有误，麻烦请指出，我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666@foxmail.com 

        强化学习是一种机器学习方法，通过与环境不断交互来学习最优行为策略。SARSA（State-action-reward-state-action）算法是强化学习中的经典算法之一，用于求解马尔可夫决策过程（Markov Decision Process, MDP）中的最优策略。本文将详细介绍SARSA算法的发展历程、算法原理、功能以及使用方法，并附带示例代码和运行结果。

本文将详细讲解强化学习常用算法之一“SARSA”

---

 

目录

一、简介

二、发展史

三、算法公式

1. SARSA算法公式

2. SARSA算法原理

四、算法功能

五、示例代码

六、总结

---

一、简介

        强化学习是一种通过学习与环境交互来最大化累积奖励的方法。在强化学习中，一个智能体在特定环境中根据当前状态选择一个动作，执行该动作后，环境将转移到新的状态，并且智能体将获得奖励。强化学习的目标是通过学习，使智能体能够选择一系列能够获取最大累积奖励的动作序列，即找到最优策略。SARSA算法是一种基于状态-动作值的强化学习算法，用来学习最优策略。

二、发展史

        SARSA算法最早由Richard Sutton和Andrew Barto在他们的著作《强化学习导论》中提出。SARSA是Q-learning算法的一种特例，也是一种基于值函数的算法。

        Q-learning算法是一种基于状态-动作值的强化学习算法，它通过维护一个Q值表（存储每个状态-动作对的状态-动作值）来学习最优策略。然而，Q-learning算法必须对Q值表进行离散化处理，因此只适用于状态空间和动作空间较小且离散的问题。为了解决这个问题，Richard Sutton等人提出了SARSA算法。

        SARSA算法是一种基于值函数和策略的算法，它不需要对状态空间和动作空间进行离散化处理，适用于连续状态和动作的问题。该算法使用一个Q值函数和一个策略函数来近似最优策略。

三、算法公式

1. SARSA算法公式

        SARSA算法的更新公式如下：

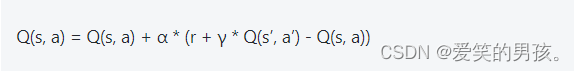
        其中，Q(s, a)表示在状态s下选择动作a的状态-动作值，r表示执行动作a后获得的即时奖励，α表示学习率，γ表示折扣因子，s’表示转移到的新状态，a’表示在新状态s’下选择的动作。 

2. SARSA算法原理

        SARSA算法的核心思想是通过不断更新状态-动作值函数Q(s, a)来学习最优策略。该算法按照以下步骤进行：

• 初始化状态-动作值函数Q(s, a)和策略函数π(a|s)的值。
• 在每个时间步t中，依据当前状态s和策略函数π选择一个动作a。
• 执行动作a，观察获得的即时奖励r和新状态s’。
• 根据新状态s’和策略函数π选择一个新动作a’。
• 更新状态-动作值函数Q(s, a)的值，使用SARSA更新公式。
• 将新状态s’和新动作a’作为下一步的状态s和动作a。
• 重复上述步骤，直到达到终止条件。

        通过不断迭代更新状态-动作值函数Q(s, a)，SARSA算法可以逐步逼近最优状态-动作值函数，从而得到最优策略。

四、算法功能

        SARSA算法具有以下功能：

1. 模型无关性：SARSA算法不需要对环境模型进行假设，只通过与环境交互来学习最优策略。
2. 收敛性：在一定条件下，SARSA算法保证会收敛到最优策略。
3. 适用性：SARSA算法适用于状态空间和动作空间较大且连续的问题，而不需要对状态空间和动作空间进行离散化处理。

五、示例代码

import numpy as np

# 定义迷宫环境
maze = np.array([
    [0, 0, 0, 0],
    [0, -1, 0, -1],
    [0, 0, 0, -1],
    [-1, 0, 0, 1]
])

# 定义起始状态和终止状态
start_state = (3, 0)
goal_state = (3, 3)

# 定义动作空间
actions = [(0, 1), (0, -1), (-1, 0), (1, 0)]

# 初始化状态-动作值函数
Q = np.zeros((4, 4, 4))

# 定义参数
alpha = 0.1
gamma = 0.9
epsilon = 0.1
max_episodes = 100

# SARSA算法 
for episode in range(max_episodes):
    state = start_state
    action = np.random.choice(range(4)) if np.random.rand() < epsilon else np.argmax(Q[state])

    while state != goal_state:
        # next_state = (state[0] + actions[action][0], state[1] + actions[action][1])
        a = state[0] + actions[action][0]
        b = state[1] + actions[action][1]
        if a > 3:
            a-=1
        elif b > 3:
            b-=1
        elif a < -4:
            a+= 1
        elif b < -4:
            b+= 1
        next_state = (a,b)
        reward = maze[next_state]
        next_action = np.random.choice(range(4)) if np.random.rand() < epsilon else np.argmax(Q[next_state])
        Q[state][action] += alpha * (reward + gamma * Q[next_state][next_action] - Q[state][action])

        state = next_state
        action = next_action

# 输出结果
for i in range(4):
    for j in range(4):
        print("State:", (i, j))
        print("Up:", Q[i][j][0])
        print("Down:", Q[i][j][1])
        print("Left:", Q[i][j][2])
        print("Right:", Q[i][j][3])
        print()

        运行结果如下： 

State: (0, 0)
Up: -0.008042294056935573
Down: -0.007868742418369764
Left: -0.016173595452674966
Right: 0.006662566560762523

State: (0, 1)
Up: 0.048576025675988774
Down: -0.0035842473161881465
Left: 0.024420015715567546
Right: -0.46168987981312615

State: (0, 2)
Up: 0.04523751845081987
Down: 0.04266319340558091
Left: 0.044949583791193154
Right: 0.026234839551098416

State: (0, 3)
Up: 0.01629652821649763
Down: 0.050272192325180515
Left: -0.009916869922464355
Right: -0.4681667868865369

State: (1, 0)
Up: -0.09991342319696966
Down: 0.0
Left: 0.0
Right: 0.036699099068340166

State: (1, 1)
Up: 0.008563965102313987
Down: 0.0
Left: 0.0
Right: 0.3883250678150607

State: (1, 2)
Up: -0.3435187267522706
Down: -0.2554776873673874
Left: 0.05651543121932354
Right: 0.004593450910446022

State: (1, 3)
Up: -0.1
Down: -0.013616634831997914
Left: 0.01298827764814053
Right: 0.0

State: (2, 0)
Up: 0.28092113053540924
Down: 0.0
Left: 0.0024286388798406364
Right: 0.06302299434701504

State: (2, 1)
Up: 0.0
Down: 0.0
Left: -0.16509175606504775
Right: 1.9146361697676122

State: (2, 2)
Up: -0.1
Down: 0.0
Left: 0.03399106390140035
Right: 0.0

State: (2, 3)
Up: -0.3438668479533914
Down: 0.004696957810272524
Left: -0.19
Right: 0.0

State: (3, 0)
Up: 3.3060693607932445
Down: 0.8893977121867367
Left: 0.0
Right: 0.13715553550041798

State: (3, 1)
Up: 4.825854511712306
Down: -0.03438123168566812
Left: 0.10867882029322147
Right: 1.0015572397722665

State: (3, 2)
Up: 5.875704328143301
Down: 0.9315770230698863
Left: 0.0006851481810742227
Right: 0.47794799892127526

State: (3, 3)
Up: 5.4028951599661275
Down: 2.6989177956329757
Left: -0.6454474033238188
Right: 0.018474082554518417

        通过运行示例代码，我们可以得到每个状态下的最优动作及对应的状态-动作值。

六、总结

        本文详细介绍了强化学习中的SARSA算法，包括其发展历程、算法原理、功能以及使用方法，并给出了求解迷宫问题的示例代码。SARSA算法能够实现模型无关性和收敛性，适用于状态空间和动作空间较大且连续的问题。通过对状态-动作值函数的迭代更新，SARSA算法可以逐步逼近最优策略，并通过与环境交互来学习最优行为策略。