动态规划基础阶段
- 前言
- 一、斐波那契数列
- 1.2、思路
- 1.2、代码实现
- 二、青蛙跳台阶问题
- 2.2、思路
- 2.2、代码实现
- 三、连续子数组的最大和
- 3.1、思路
- 3.2、代码实现
- 总结
前言
动态规划(Dynamic Programming,简称 DP)是一种解决多阶段决策过程最优化问题的方法。它是一种将复杂问题分解成重叠子问题的策略,通过维护每个子问题的最优解来推导出问题的最优解。
动态规划的主要思想是利用已求解的子问题的最优解来推导出更大问题的最优解,从而避免了重复计算。因此,动态规划通常采用自底向上的方式进行求解,先求解出小规模的问题,然后逐步推导出更大规模的问题,直到求解出整个问题的最优解。
动态规划通常包括以下几个基本步骤:
- 定义状态:将问题划分为若干个子问题,并定义状态表示子问题的解;
- 定义状态转移方程:根据子问题之间的关系,设计状态转移方程,即如何从已知状态推导出未知状态的计算过程;
- 确定初始状态:定义最小的子问题的解;
- 自底向上求解:按照状态转移方程,计算出所有状态的最优解;
- 根据最优解构造问题的解。
动态规划可以解决许多实际问题,例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。同时,动态规划也是许多其他算法的核心思想,例如分治算法、贪心算法等。
动态规划是一种解决多阶段决策过程最优化问题的方法,它将复杂问题分解成重叠子问题,通过维护每个子问题的最优解来推导出问题的最优解。动态规划包括定义状态、设计状态转移方程、确定初始状态、自底向上求解和构造问题解等步骤。动态规划可以解决许多实际问题,也是其他算法的核心思想之一。
一、斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1;
F(N) = F(N - 1) + F(N - 2), 其中 N > 1。
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:1
示例 2:
输入:n = 5
输出:5
来源:力扣(LeetCode)。
1.2、思路
斐波那契数的边界条件是F(0)=0 和 F(1)=1。当 n>1 时,每一项的和都等于前两项的和,因此有如下递推关系:
F(n)=F(n−1)+F(n−2)
由于斐波那契数存在递推关系,因此可以使用动态规划求解。动态规划的状态转移方程即为上述递推关系,边界条件为 F(0) 和 F(1)。
根据状态转移方程和边界条件,可以得到时间复杂度和空间复杂度都是 O(n) 的实现。由于 F(n) 只和
F(n−1) 与 F(n−2) 有关,因此可以使用「滚动数组思想」把空间复杂度优化成 O(1)。如下的代码中给出的就是这种实现。
计算过程中,答案需要取模 1e9+7。
1.2、代码实现
class Solution {
public:
int fib(int n) {
if(n<2)
return n;
int pre=0,pre2=1;
int cur=0;
for(int i=2;i<=n;i++)
{
cur=(pre+pre2)%(1000000007);
pre=pre2;
pre2=cur;
}
return cur;
}
};
时间复杂度:O(n)。
空间复杂度:O(1)。
二、青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
示例 3:
输入:n = 0
输出:1
来源:力扣(LeetCode)。
2.2、思路
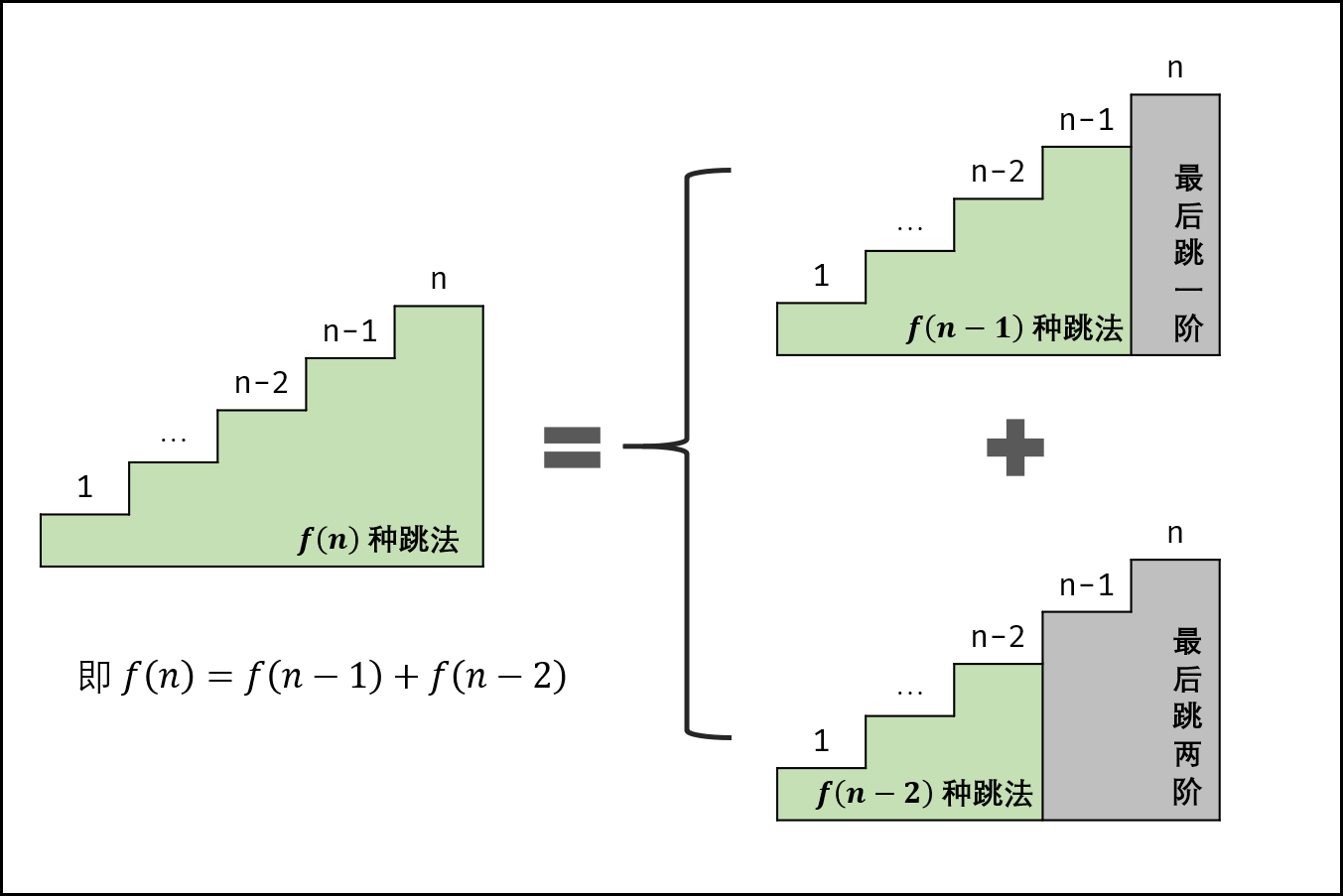
设跳上 n 级台阶有 f(n) 种跳法。在所有跳法中,青蛙的最后一步只有两种情况: 跳上 1 级或 2 级台阶。
- 当为 1 级台阶: 剩 n−1 个台阶,此情况共有 f(n−1) 种跳法;
- 当为 2 级台阶: 剩 n−2 个台阶,此情况共有 f(n−2) 种跳法。
f(n) 为以上两种情况之和,即 f(n)=f(n−1)+f(n−2) ,以上递推性质为斐波那契数列。本题可转化为 求斐波那契数列第 n 项的值 ,唯一的不同在于起始数字不同。
- 青蛙跳台阶问题: f(0)=1 , f(1)=1 , f(2)=2 ;
- 斐波那契数列问题: f(0)=0 , f(1)=1 , f(2)=1 。
2.2、代码实现
class Solution {
public:
int numWays(int n) {
if(n<2)
return 1;
int pre=1,pre2=1;
int cur=1;
for(int i=2;i<=n;i++)
{
cur=(pre+pre2)%(1000000007);
pre=pre2;
pre2=cur;
}
return cur;
}
};
时间复杂度:O(n)。
空间复杂度:O(1)。
三、连续子数组的最大和
输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
来源:力扣(LeetCode)。
3.1、思路
动态规划是本题的最优解法。
动态规划解析:
状态定义: 设动态规划列表 dp[i] 代表以元素 nums[i] 为结尾的连续子数组最大和。
为何定义最大和 dp[i] 中必须包含元素 nums[i] :保证 dp[i] 递推到 dp[i+1] 的正确性;如果不包含
nums[i] ,递推时则不满足题目的 连续子数组 要求。
转移方程: 若 dp[i−1]≤0 ,说明 dp[i−1] 对 dp[i] 产生负贡献,即 dp[i−1]+nums[i] 还不如 nums[i] 本身大。
当 dp[i−1]>0 时:执行 dp[i]=dp[i−1]+nums[i] ;
当 dp[i−1]≤0 时:执行 dp[i]=nums[i] ;
初始状态:
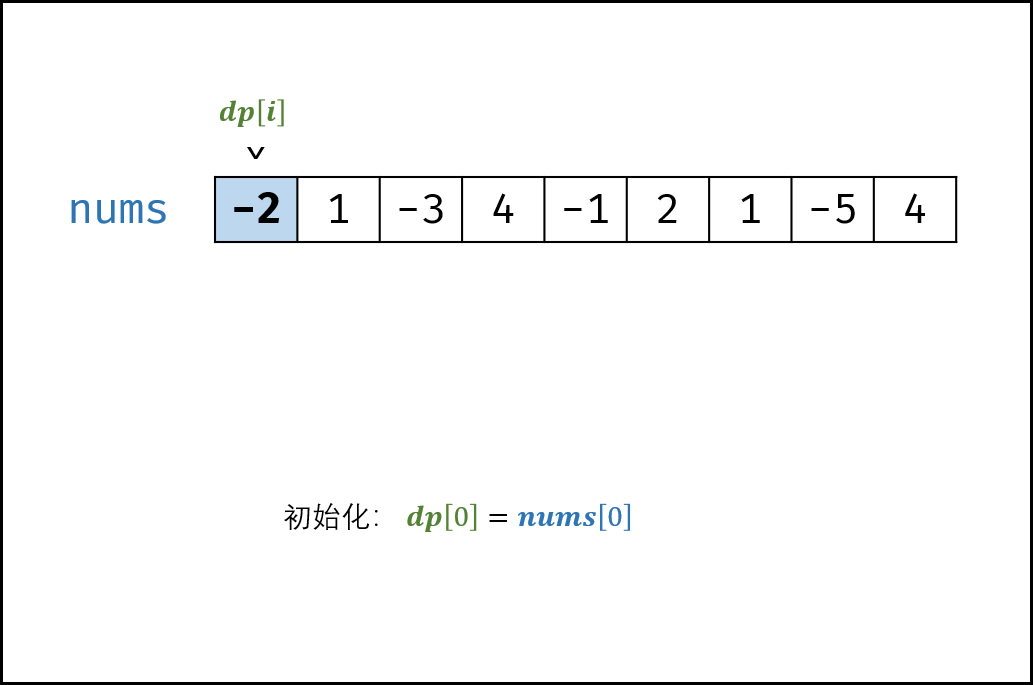
dp[0]=nums[0],即以 nums[0] 结尾的连续子数组最大和为 nums[0] 。
返回值: 返回 dp 列表中的最大值,代表全局最大值。
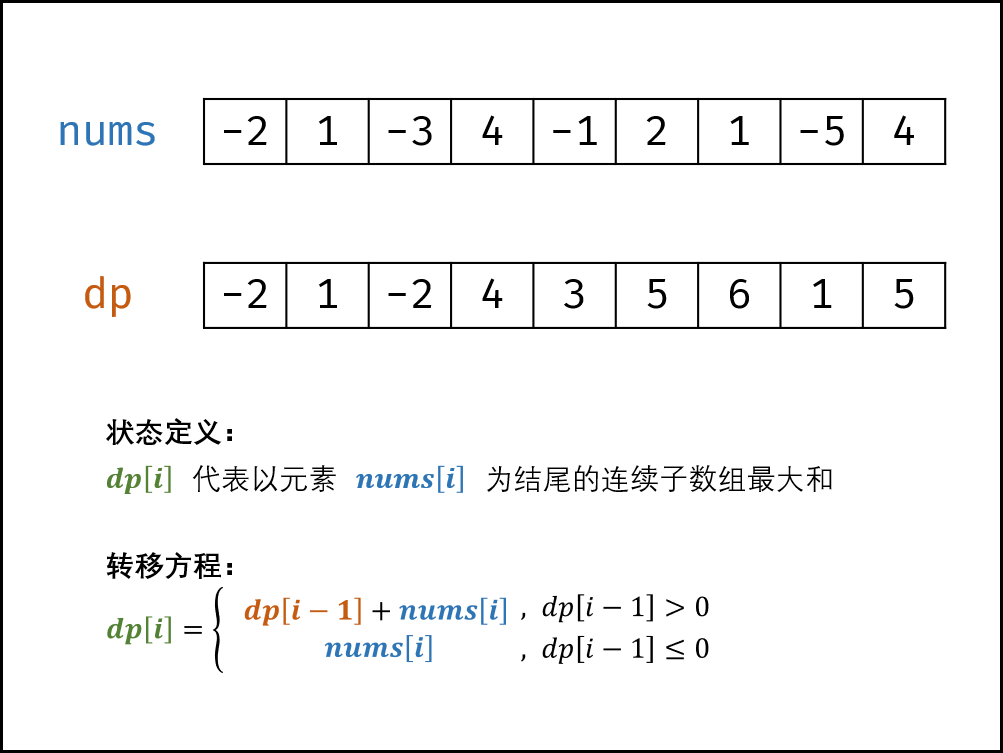
空间复杂度降低:
由于 dp[i] 只与 dp[i−1] 和 nums[i] 有关系,因此可以将原数组 nums 用作 dp 列表,即直接在 nums 上修改即可。
由于省去 dp 列表使用的额外空间,因此空间复杂度从 O(N) 降至 O(1) 。
3.2、代码实现
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n=nums.size();
int res=nums[0];
for(int i=1;i<n;i++)
{
nums[i]+=max(nums[i-1],0);
res=max(res,nums[i]);
}
return res;
}
};
时间复杂度:O(n)。
空间复杂度:O(1)。
总结
动态规划(Dynamic Programming)是一种解决多阶段决策最优化问题的方法,它将复杂问题分解成重叠子问题并通过维护每个子问题的最优解来推导出问题的最优解。动态规划可以解决许多实际问题,例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。
动态规划的基本思想是利用已求解的子问题的最优解来推导出更大问题的最优解,从而避免了重复计算。它通常采用自底向上的方式进行求解,先求解出小规模的问题,然后逐步推导出更大规模的问题,直到求解出整个问题的最优解。
动态规划通常包括以下几个基本步骤:
- 定义状态:将问题划分为若干个子问题,并定义状态表示子问题的解;
- 定义状态转移方程:根据子问题之间的关系,设计状态转移方程,即如何从已知状态推导出未知状态的计算过程;
- 确定初始状态:定义最小的子问题的解;
- 自底向上求解:按照状态转移方程,计算出所有状态的最优解;
- 根据最优解构造问题的解。
动态规划的时间复杂度通常为 O ( n 2 ) O(n^2) O(n2)或 O ( n 3 ) O(n^3) O(n3),空间复杂度为O(n),其中n表示问题规模。在实际应用中,为了减少空间复杂度,通常可以使用滚动数组等技巧来优化动态规划算法。