Kasiski

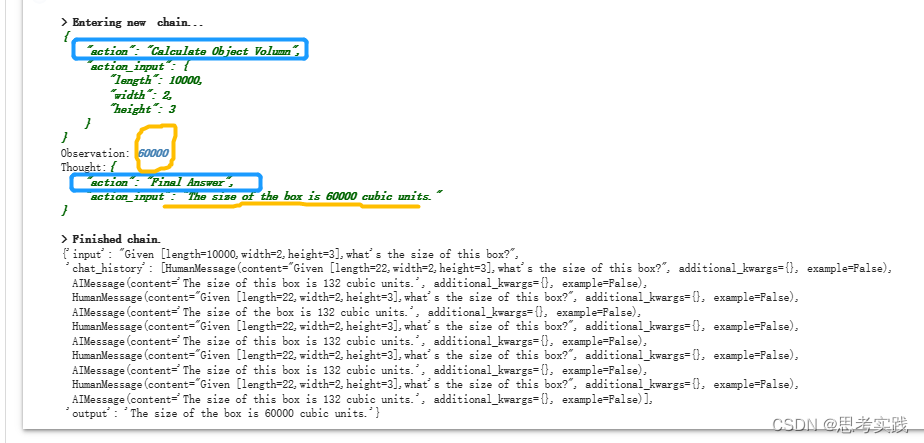
Kasiski是辅助破解Vigenere的前提工作，Kasiski是猜测加密者使用Vigenere密码体系的密钥的长度，Kasiski只是猜测长度而已，所以说是辅助破解Vigenere

若密文中出现两个相同的密文段(密文段的长度m>2)，则它们对应的明文（及密钥）将以很大的概率相同（后文有一个该概率的计算）。
针对多表密码，首要的是得到秘钥字的长度，进一步判断密钥字的长度是否为：m=gcd(d1,d2,…,di) d：为密文片段直接的距离。
我们可以猜测秘钥字的长度m可能是d1,d2,…,di 最大公因子。
这就是Kasiski测试法。
——出自我的密码学老师PPT原文

我的理解
Kasiski的主要功劳即使帮助破解Vigenere密码找到密钥长度，具体如何找的
- 找相同的密文片段（片段当然是两个以上才算，这个具体找多少个自己写算法的时候自己确认，或者设置一个参数手动输入）
- 记录相同片段出现的位置（记录的是片段第一个字母出现的位置作为整个片段出现的位置）
- 当然考虑到的肯定就是出现次数最多的了（这个算法实现还是比较费脑子）
- 当然在找的过程中还要记录下每个出现的位置，然后用这个位置求最大公因数，那么这个最大公因数就是最有可能的密钥长度
为什么最大公因数就是有可能是密钥长度
因为在Vigenere加密中，使用的是多表加密，每一个表都是凯撒密码，使用的都是同一个字母加密，不同表只是在密钥串中的不同字母加密而已。所以假如说有相同的片段出现，就可以推断出相同密钥字母出现的周期，然后周期就是这个密钥的长度，因为Vigenere就是周期性的使用密钥对明文进行加密，下面我密码学老师的PPT对这个说法有一个很好的解释，一眼就看出是周期性的时候密钥加密。

这也很明显的点名了为啥Vigenere中要分组加密，因为分好组之后每一组第一个字母使用的都是同一个密钥加密，所以也就所谓的单表对应凯撒密码加密，Vigenere使用多个凯撒加密表。

找到出现相同片段

算法实现
- 困难：如何找到出现次数最多的片段（字母串）？
  Python真是帮了很大的一个忙了，因为有find内置函数省了我很多工作，因为只要用好下标就能够找到所有出现过的单词
- 我的想法
  首先是传入一个字符串，然后a参数代表找的最短连续出现的片段长度，b代表最长的出现片段长度。
  为什么要这么做呢：因为如果不设置一个参数人为的介入这个程序会无限制的找下去，直到整个字符串都会find一遍，这样式毫无意义的，还很浪费性能与时间。
  由于find内置函数返回的值就是要找的片段第一个字母出现的下标，因此我甚至省去写如何找下标的步骤（在此特地感谢Python开发者们）
  - 找到下标之后我将其存进一个字典，字典的键是字符片段，值就是该片段在文本中出现的位置的各个下标，然后如果要记录出现此处就计算该列表的长度就是出现的次数了。
  - 这里我配合find内置函数采用了切片的方式进行找同片段，从给出的a参数最短的片段作为开头，那么在文本中开头0~a长度的就不用找，以此为第一个单词，然后用这个单词在后面find如果find到了表示OK找到的，存find函数返回的出现的下标，全部找完之后，使用a长度跨越a个步数，意思是这个片段已经全部找到了，往后的就是该片段之后的要重复上述操作。
  - 这里我当时想了一个我自认为很妙的方法：我遍历的是传入的ab参数，因为是人为介入的，所以我应该是从a长度的开始找，这里我的目的是给出一个步长变量step，为的就是让第二层遍历在找完某个step长的单词片段之后跨越step长度继续往后找，然后这个step还给当找到一个之后继续往后找的时候就从找到的片段的下标再加一个step然后就可以将其继续往后找，这里我认为是减少了再次遍历的次数，我个人是觉得优化了一下
  - index = mess.find(mess[i:i + step], index + 1)解读
    这个一个就是我认为写的很好的一点，mess是全部文本，首先mess[i:i+step]是表示当前要找的片段，由于是while是确保了后面会有相同片段的，然后index+1代表找第二次的时候，index已经记录第一次找到的下标，这里第二次找就是从已经找到的片段的后面找起。

def findSameWords(self, mess, a, b):
    # 找出现次数最多的字符，返回他所有下标和字符本身

    dit_wordCount = {}  # 保存不同长度的字符出现次数最多的,键：'字符'，值：[出现的次数, [每次出现的下标]]

    for step in range(a, b + 1):
        for i in range(len(mess) - step):
            # 每一次进入if都是全局搜索,如果之前判断过存放在字典中没有该字符串就继续全局文本中去find
            if mess[i:i + step] not in dit_wordCount.keys():
                ''' 
                    意思是mess从step+i开始找有没有和mess[i:i+step]该字符串相同的字符串
                    同时保证了i是递增，并且mess截串是从一开始的下标0开始找，
                    整个mess文本里面又是从i+step开始往后findmess截串
                    ↓ 
                '''
                #这里是先试探一下是否存在，存在就做初始化操作，否则-1的话就不用继续进入
                index = mess.find(mess[i:i + step], i + step) 
                if index != -1: dit_wordCount[mess[i:i + step]] = [1, [i + 1]]  # 当该字符不止出现一次的时候就初始化该字符的字典键
                while index != -1:  # 找到了
                    dit_wordCount[mess[i:i + step]][0] += 1
                    dit_wordCount[mess[i:i + step]][1].append(index + 1)
                    index = mess.find(mess[i:i + step], index + 1)  # 继续找
    return dit_wordCount

找到相同长度不同片段中出现次数最多的片段

解释：这里使用的是上面存的字典，然后进行这下面的操作

在这里说的是找到相同长度片段中出现次数最多的，意思就是在一篇文本中相同片段的很多，然后片段长度相同的也很多，这里要找的就是从这些不同片段但是长度相同的片段中找到频率最多的，这里就相当于打擂台操作了。
然后由于字典中已经完成了大部分工作，在这一步中只需要将其遍历然后将所需的数据放进另一个字典中即可。
在本步骤中要找的数据：[(片段, [出现次数，[每次出现的下标]]) , … ]

第一步是先统计每个片段出现频率并找出最大的那个（这里会出现很多，因此需要有之后的第二步）
代码如下：满满的注释，感谢自己。

 def caltFrequence(self, dit_wordCount):
     selectWord = []  # 保存挑选出来符合条件的单词
     last_len = 0  # 字典中字符串长度相同中最后一个 ，用于保存每一次循环中字符长度，利用字符长度改变来判断是否进行完成一轮该字符长度的筛选操作
     maxcount = 0  # 该字符长度的字典里面出现最大次数
     temp = None
     for item in dit_wordCount.items():  # 感谢开发者们让字典从Python3.6版本开始变得可以有顺序了，节省了我写代码再次区分字符串长度不同的
         if len(item[0]) > last_len and temp != None and self.sb_MaxKeyCurrtime.value() <= temp[1][0]:
             # 判断是否在该字符长度内出现次数最多，比如字符串长度为3中，出现次数最多的为CHR那么该字符就保存下来，其他就丢掉
             # len(item[0]) > last_len 假如字符串长度发生变化就表示进入了下一个不同的字符串长度的域，需要把上一个temp存下来的数据加进去
             # temp != None判断是否是第一次进入
             # self.sb_MaxKeyCurrtime.value() <= temp[1][0]控制至少出现的次数
             selectWord.append(temp)
         if item[1][0] > maxcount and len(item[0]) == last_len or len(item[0]) > last_len:
             # 假如该item中出现次数比之前相同字符的还要多，就存入该字符的数据 。
             # len(item[0]) > last_len控制是否是字符长度有所改变，或者是否是第一次进入
             last_len = len(item[0])
             maxcount = item[1][0]
             temp = item

     # print(selectWord)
     return selectWord
     # 每一项的结构就是： [('CHR', [5,    [1, 166, 236, 276, 286] ]  )，......]
     #                   字符  出现次数   对应字符在密文中出现的下标位置

第二步
我是通过一个类中一个变量接收的猜测的最长长度
可能会有疑惑：刚刚不是找最短出现的次数吗，现在怎么又是最长了。
当我们在最短中往后找的时候，可能会出现很长的出现片段，由于我们找的不仅仅是一个长度的片段的，我还找了其他不同长度的片段，那么就可能会导致找到一个很长的，但同时又满足最短出现的次数，然后又是在该片段中相同长度的不同片段中出现的次数最多，那么就是属于符合条件的了。
那么在这一步中就是人为的介入，将认为没有必要的比如：很长一段片段，然后出现次数刚好满足最短的出现次数，并且你觉得我们的加密方没有闲到用这么长的密钥加密的时候你就可以切除掉这个隐患。

代码如下：

def getMaxNumList(self, selectData):  # 每一项的结构就是： [('CHR', [5,    [1, 166, 236, 276, 286] ]  )，......]
    # num_list = []
    keymaxlen = self.sb_choiceMaxKeylen.value()  # 允许猜测密钥的最长长度，也就是最大公因数
    ch_maxnum = []
    for item in selectData:
        # 拆包，提取出计算最大公因数的距离数字
        ch, date = item
        count, index_list = date
        # if self.sb_MaxKeyCurrtime.value() > count-1: continue
        print(index_list)
        distance_list = []
        for j in range(len(index_list) - 1):
            distance_list.append(index_list[j + 1] - index_list[0])
        num = distance_list[0]
        for j in range(1, len(distance_list)):
            num = math.gcd(num, distance_list[j])
        # num_list.append(num)
        if num > keymaxlen:
            selectData.remove(item)
        else:
            ch_maxnum.append([ch, num])
    return ch_maxnum

到这一步Kasiski测试法基本就结束了，测试法顾名思义测试的，还不是很有力的证据，因此在这里使用的定义仅仅是找到出现次数最多的相同片段然后将其位置下标做一个gcd求最大公因数即猜测为密钥长度（如果是很普通的明文与密钥加密的Vigenere一般到这一步基本可以确认长度了），如果是一篇很乱的，基本没有出现重复的或者很短一篇文章这个测试法就很局限了，很容易就失效的一个方法，而且出现的频次相同但是计算出来的gcd不同更难搞，因为密钥长度这时候就有两种方案了
如果说有两种方案的密钥猜测出来，这时候就需要另一个方法了，那就是计算重合指数（这个重合指数靠的纯纯是已知的一般文章中的字母概率进行统计，但是对于一般的但是有两种密钥方案的就可以很好的区分出到底哪一个更接近真实的密钥长度。）
所以Kasiski测试法测试出来的长度是否真的是密钥长度还需要重合指数来进一步验证