这里是Eigen库的一些基础语法，摘自《视觉SLAM十四讲》，修改了书中代码的一些bug，部分地方添加了一些自己的理解。

头文件相关

#include <Eigen/Core>	// Eigen 核心部分
#include <Eigen/Dense>	// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Geometry>	// 提供了各种旋转和平移的表示

CMake注意事项

include_directories("/usr/include/eigen3")

定义相关

定义一个$2\times 3$的float矩阵：

Eigen::Matrix<float, 2, 3> matrix_23;

定义一个3维的double向量：

Eigen::Vector3d v_3d;
// 等价于：Matrix<double, 3, 1> vd_3d;

定义一个$3\times 3$的double矩阵，同时初始化为0：

Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero();;

定义一个大小不定的矩阵：

// 方式1
Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> matrix_dynamic;
// 方式2
Eigen::MatrixXd matrix_x;

初始化方法

// 输入数据（初始化）
matrix_23 << 1, 2, 3, 4, 5, 6;
// 输出
cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;

输出：

matrix 2x3 from 1 to 6: 
1 2 3
4 5 6

初始化为随机数：

matrix_33 = Eigen::Matrix3d::Random();

访问矩阵元素

用括号来访问矩阵第i行，第j列的元素（i, j起始均为0）：

matrix_23(i, j)

显式类型转换

Eigen不允许两种不同类型的矩阵相乘，必须要做显式类型转换，如：

Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;

一些矩阵操作

转置：

matrix_33.transpose()

求各元素和：

matrix_33.sum()

求迹：

matrix_33.trace()

求逆矩阵：

matrix_33.inverse()

求行列式：

matrix_33.determinant()

求特征值和特征向量：

// 实对称矩阵可以保证对角化成功
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
// 特征值
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
// 特征向量
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;

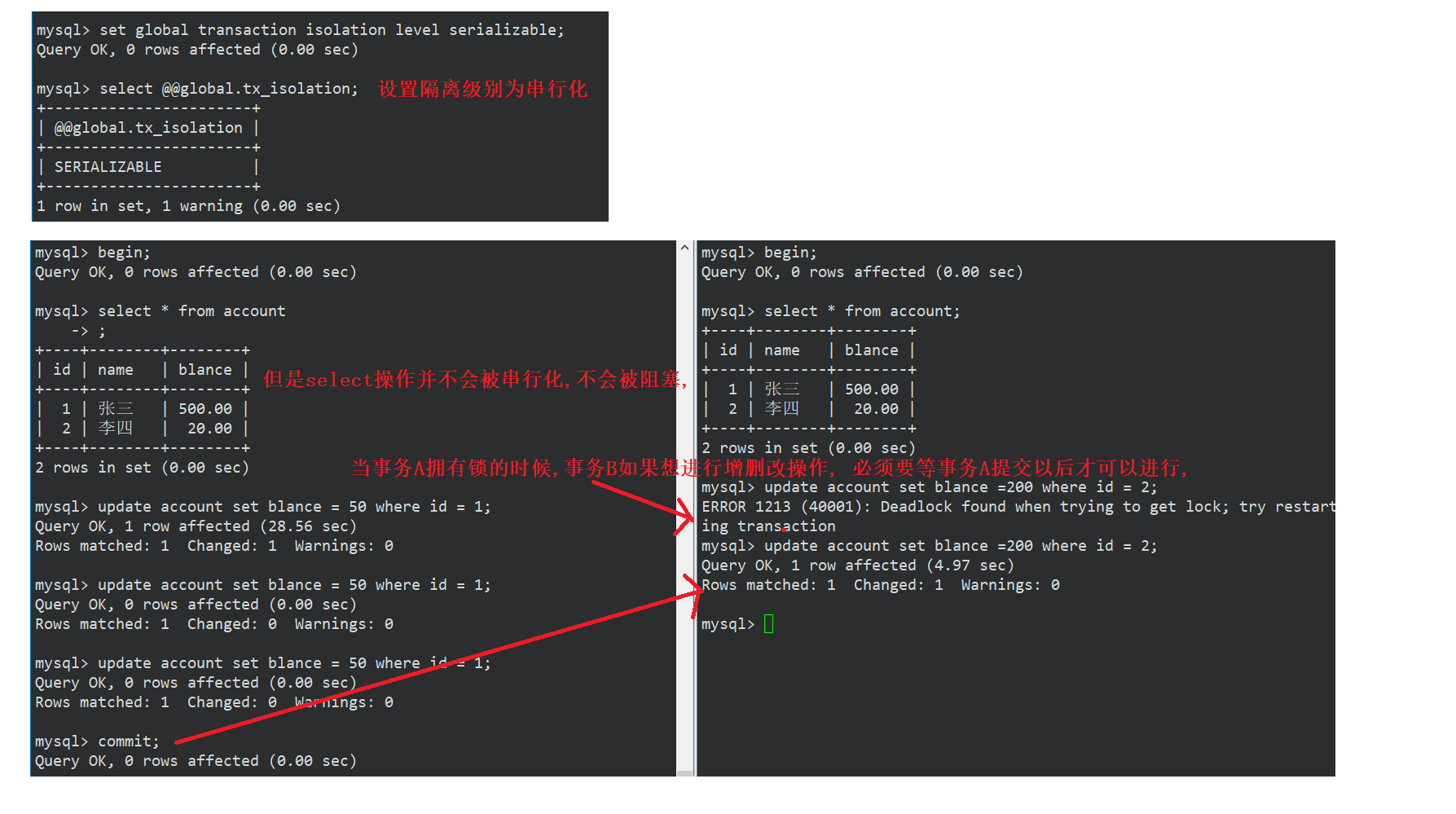
解方程

目标：求解matrix_NN * x = v_Nd这个方程

// 首先定义matrix_NN
Eigen::Matrix<double, 50, 50> matrix_NN = Eigen::MatrixXd::Random(50, 50);
// 然后定义x
Eigen::Matrix<double, 50, 1> x

解法1：直接求逆（慢）

// 直接求逆
x = matrix_NN.inverse() * v_Nd;

解法2：QR分解（快）

x = matrix_NN.colPivHouseholderQr().solve(v_Nd);

解法3：cholesky分解（快，要求正定矩阵）

x = matrix_NN.ldlt().solve(v_Nd);

旋转矩阵

定义一个$3\times 3$的double旋转矩阵，同时初始化为单位阵：

Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();

旋转向量

定义一个绕z轴旋转45°的旋转向量：

Eigen::AngleAxisd rotation_vector(M_PI / 4, Eigen::Vector3d(0, 0, 1));

注意：旋转向量的底层不直接是Matrix，但运算时可以当作旋转矩阵（因为重载了运算符）

Eigen::Vector3d v(1, 0, 0);
Eigen::Vector3d v_rotated = rotation_vector * v;

用matrix()或toRotationMatrix()可以转换成旋转矩阵：

rotation_matrix = rotation_vector.matrix()
rotation_matrix = rotation_vector.toRotationMatrix();

旋转矩阵转欧拉角

Eigen::Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); 
// (2, 1, 0)分别对应(X, Y, Z)，说明按ZYX顺序旋转

欧式变换、仿射变换、射影变换

定义一个 $4\times 4$ 欧氏变换矩阵，同时初始化为单位阵：

// 虽然说是3d，实际上是4×4的矩阵
Eigen::Isometry3d T = Eigen::Isometry3d::Identity();
// 按照rotation_vector进行旋转
T.rotate(rotation_vector);
// 把平移向量设成(1,3,4)
T.pretranslate(Vector3d(1, 3, 4));

定义一个 $4\times 4$ 仿射变换矩阵：Eigen::Affine3d，其余操作与Eigen::Isometry3d一致。有的时候会用Eigen::Affine3d来代替Eigen::Isometry3d。

定义一个 $4\times 4$ 射影变换矩阵：Eigen::Projective3d，其余操作与Eigen::Isometry3d一致。$\mathbf{A}$ 和 $\mathbf{t}$ 的赋值方式与Eigen::Isometry3d一致，尚不知道如何赋值${\mathbf{a}}^T$。实际上也不怎么常用。

用变换矩阵进行坐标变换

Eigen::Vector3d v_transformed = T * v; 	// 相当于R * v + t

四元数

用旋转向量来初始化四元数（反之亦可）：

Eigen::Quaterniond q = Eigen::Quaterniond(rotation_vector);

用旋转矩阵来初始化四元数（反之亦可）：

q = Eigen::Quaterniond(rotation_matrix);

普通初始化四元数的方法：

// (w, x, y, z)
Eigen::Quaterniond(0, 1, 0, 0)

cout四元数的方法：

// (x, y, z, w)
cout << q.coeffs().transpose() << endl;

注意：

• coeffs的顺序是$(x,y,z,w)$，$w$为实部，前三者为虚部。这个顺序也是内部存储和运算的顺序。
• 利用Quaterniond()初始化的顺序为$(w,x,y,z)$，顺序是不一样的。

共轭四元数：

// (w, -x, -y, -z)
q.conjugate()

用四元数来旋转一个向量（乘法被重载了，这里的乘法不表示四元数乘法）：

// 表示旋转的四元数要归一化
q.normalize();
// 使用四元数旋转一个向量
v_rotated = q * v; // 注意数学上是q * Quaterniond(0, 1, 0, 0) * q共轭

出处：