VTK-vtkPointInterpolator/vtkInterpolatorKernel

news2024/9/22 17:26:30

欢迎大家加入社区，雪易VTK社区-CSDN社区云

前言：目前在做模型的ReMesh，在研究这个接口，希望能有所帮助。

 vtkPointInterpolator

描述：

变量：

Strategy：MASK_POINTS, NULL_VALUE, CLOSEST_POINT

指定插补过程中遇到“空”点时使用的策略。当局部邻域（要进行插值的相邻点的邻域）为空时，就会出现空点。若策略设置为MaskPoints，则创建一个输出数组，将点标记为有效或无效。若策略设置为NullValue(默认值)，则输出数据值设置为NullPoint值（在输出点数据中指定）。若策略为ClosePoint，则简单地使用最近的点来执行插值。

 

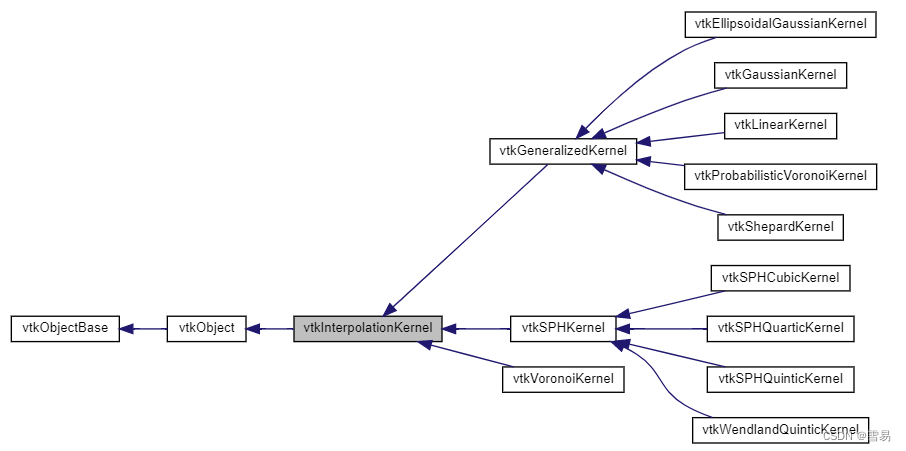
目录

vtkInterpolationKernel

 vtkGeneralizedKernel

vtkEllipsoidalGaussianKernel

vtkGaussianKernel

vtkLinearKernel

vtkProbabilisticVoronoiKernel

vtkShepardKernel

vtkSPHKernel

 

vtkInterpolationKernel

 

 vtkGeneralizedKernel

 描述：vtkGeneralizedKernel是一个抽象类，具有重要的属性：权值是归一化的；基础的占用空间是可配置的；概率加权函数可用于偏爱某些权重。

 权值是归一化的

归一化权值即Sum(w_i) = 1；这确保了插值具有良好的质量。

 基础的占用空间是可配置的

插值footprint是用于执行插值过程的点集。例如可以选择基于半径的内核和基于N个邻域点的内核。内核的性能和数学属性会根据选择的内核类型而有很大的不同。例如基于半径的内核，如果半径过大，则算法将以n^3执行。

在高级用法中，可以将概率函数应用于计算插值权重。概率函数是对某点的数据准确的置信度估计。一个典型的应用是当激光扫描用于获取点测量时，它返回法线，表示与直接的、接近正交的命中相比的掠射返回。

常用方法:

ComputeBasis

    /**
   * Based on the kernel style, invoke the appropriate locator method to
   * obtain the points making up the basis. Given a point x (and optional
   * associated point id), determine the points around x which form an
   * interpolation basis. The user must provide the vtkIdList pIds, which
   * will be dynamically resized as necessary. The method returns the number
   * of points in the basis. Typically this method is called before
   * ComputeWeights(). Note that ptId is optional in most cases, although in
   * some kernels it is used to facilitate basis computation.
   */
    //基于内核样式，调用适当的定位器方法来获得组成Basis的点。给定一个点x(和可选的关联点id)，确定在
    //在x周围形成插值Basis的点。用户必须提供pIds，它将根据需要动态调整大小。
    //该方法返回Basis中的点数，通常在ComputeWeights()之前调用该方法。
  vtkIdType ComputeBasis(double x[3], vtkIdList* pIds, vtkIdType ptId = 0) override;

 ComputeWeights

/**
 * Given a point x, a list of basis points pIds, and a probability
 * weighting function prob, compute interpolation weights associated with
 * these basis points.  Note that basis points list pIds, the probability
 * weighting prob, and the weights array are provided by the caller of the
 * method, and may be dynamically resized as necessary. The method returns
 * the number of weights (pIds may be resized in some cases). Typically
 * this method is called after ComputeBasis(), although advanced users can
 * invoke ComputeWeights() and provide the interpolation basis points pIds
 * directly. The probably weighting prob are numbers 0<=prob<=1 which are
 * multiplied against the interpolation weights before normalization. They
 * are estimates of local confidence of weights. The prob may be nullptr in
 * which all probabilities are considered =1.
 */
//给定一个点x，一组几点pIds和一个概率加权函数probb，计算这些基点相关的插值权重。
//该方法返回权重的数量（在某些情况下可以调整pIds的大小），通常在ComputeBasis()之后调用。
//加权概率prob是数字0<= probb <=1，在归一化之前乘以插值权重。它们是加权局部置信度的估计。
//prob可能是nullptr，其中所有概率都被认为是=1。
virtual vtkIdType ComputeWeights(
  double x[3], vtkIdList* pIds, vtkDoubleArray* prob, vtkDoubleArray* weights) = 0;

KernelStyle：RADIUS, N_CLOSEST

/**
 * Specify the interpolation basis style. By default, a Radius style is
 * used (i.e., the basis is defined from all points within a specified
 * radius). However, it is also possible to select the N closest points
 * (NClosest). Note that in most formulations the Radius style is assumed
 * as it provides better mathematical properties. However, for convenience
 * some bases are easier to use when the N closest points are taken.
 */
//指定插值基样式。默认情况下，使用半径样式(即，从指定半径内的所有点定义基础)。但是，也可以选择N个
//最近的点(nnearest)。
//请注意，在大多数公式中采用半径样式，因为它提供了更好的数学属性。
//然而，为了方便起见，当取N个最近的点时，一些基底更容易使用。
vtkSetMacro(KernelFootprint, int);
vtkGetMacro(KernelFootprint, int);
void SetKernelFootprintToRadius() { this->SetKernelFootprint(RADIUS); }
void SetKernelFootprintToNClosest() { this->SetKernelFootprint(N_CLOSEST); }

NormalizeWeights权重归一化

/**
 * Indicate whether the interpolation weights should be normalized after they
 * are computed. Generally this is left on as it results in more reasonable
 * behavior.
 */
//插值权重计算后是否应归一化。通常情况下，这是保留的，因为它会导致更合理的行为。
vtkSetMacro(NormalizeWeights, bool);

vtkEllipsoidalGaussianKernel

描述：vtkEllipsoidalaussianKernel是一个插值核，返回由半径R定义的椭球中所有点的权重（结合法线或者标量数据）。“pancake”权重（与最小椭球轴平行的局部法线）；“needle”权重（与最大椭球轴平面的局部法线）。vtkGaussianKernel可以更有效的计算球形高斯权重。 

vtkGaussianKernel

描述：vtkGaussianKernel是一个插值核，它简单地返回由半径R定义的球中所有点的权重。权重计算为:exp(-(s*r/ R)^2)，其中r是从要插值的点到r内邻近点的距离。锐度s只是影响高斯函数的下降速率。(更通用的高斯内核可以从vtkEllipsoidalGaussianKernel中获得。)

vtkIdType vtkGaussianKernel::ComputeWeights(
  double x[3], vtkIdList* pIds, vtkDoubleArray* prob, vtkDoubleArray* weights)
{
  vtkIdType numPts = pIds->GetNumberOfIds();
  double d2, y[3], sum = 0.0;
  weights->SetNumberOfTuples(numPts);
  double* p = (prob ? prob->GetPointer(0) : nullptr);
  double* w = weights->GetPointer(0);
  double f2 = this->F2;

  for (vtkIdType i = 0; i < numPts; ++i)
  {
    vtkIdType id = pIds->GetId(i);
    this->DataSet->GetPoint(id, y);
    d2 = vtkMath::Distance2BetweenPoints(x, y);

    if (vtkMathUtilities::FuzzyCompare(
          d2, 0.0, std::numeric_limits<double>::epsilon() * 256.0)) // precise hit on existing point
    {
      pIds->SetNumberOfIds(1);
      pIds->SetId(0, id);
      weights->SetNumberOfTuples(1);
      weights->SetValue(0, 1.0);
      return 1;
    }
    else
    {
      w[i] = (p ? p[i] * exp(-f2 * d2) : exp(-f2 * d2));
      sum += w[i];
    }
  } // over all points

  // Normalize
  if (this->NormalizeWeights && sum != 0.0)
  {
    for (vtkIdType i = 0; i < numPts; ++i)
    {
      w[i] /= sum;
    }
  }

  return numPts;
}

vtkLinearKernel

描述：vtkLinearKernel是一个插值核，它为Basis中所有点的均值。

vtkIdType vtkLinearKernel::ComputeWeights(
  double*, vtkIdList* pIds, vtkDoubleArray* prob, vtkDoubleArray* weights)
{
  vtkIdType numPts = pIds->GetNumberOfIds();
  double* p = (prob ? prob->GetPointer(0) : nullptr);
  weights->SetNumberOfTuples(numPts);
  double* w = weights->GetPointer(0);
  double weight = 1.0 / static_cast<double>(numPts);

  if (!prob) // standard linear interpolation
  {
    for (vtkIdType i = 0; i < numPts; ++i)
    {
      w[i] = weight;
    }
  }

  else // weight by probability
  {
    double sum = 0.0;
    for (vtkIdType i = 0; i < numPts; ++i)
    {
      w[i] = weight * p[i];
      sum += w[i];
    }
    // Now normalize
    if (this->NormalizeWeights && sum != 0.0)
    {
      for (vtkIdType i = 0; i < numPts; ++i)
      {
        w[i] /= sum;
      }
    }
  }

  return numPts;
}

vtkProbabilisticVoronoiKernel

描述：vtkProbabilisticVoronoiKernel是一个插值核，它从点的邻域中最近的加权点进行插值。权重指的是可以提供给ComputeWeights()方法的概率权重。

如果没有定义概率权重，则内核提供与vtkVoronoiKernel相同的结果，只是效率较低。

vtkIdType vtkProbabilisticVoronoiKernel::ComputeWeights(
  double x[3], vtkIdList* pIds, vtkDoubleArray* prob, vtkDoubleArray* weights)
{
  vtkIdType numPts = pIds->GetNumberOfIds();
  double* p = (prob ? prob->GetPointer(0) : nullptr);
  double highestProbability = VTK_FLOAT_MIN;
  vtkIdType id, mostProbableId = 0;

  if (p) // return the point in the neighborhood with the highest probability
  {
    for (vtkIdType i = 0; i < numPts; ++i)
    {
      if (p[i] > highestProbability)
      {
        mostProbableId = pIds->GetId(i);
        highestProbability = p[i];
      }
    }
  }

  else // return the closest point in the footprint provided
  {
    double y[3], d, minD = VTK_FLOAT_MAX;
    for (vtkIdType i = 0; i < numPts; ++i)
    {
      id = pIds->GetId(i);
      this->DataSet->GetPoint(id, y);
      d = vtkMath::Distance2BetweenPoints(x, y);
      if (vtkMathUtilities::FuzzyCompare(d, 0.0,
            std::numeric_limits<double>::epsilon() * 256.0)) // precise hit on existing point
      {
        mostProbableId = id;
        break;
      }
      else if (d <= minD)
      {
        mostProbableId = id;
        minD = d;
      }
    } // over all points
  }

  // Okay let's get out
  pIds->SetNumberOfIds(1);
  pIds->SetId(0, mostProbableId);
  weights->SetNumberOfTuples(1);
  weights->SetValue(0, 1.0);

  return 1;
}

vtkShepardKernel

描述：vtkShepardKernel是一个使用Shepard方法进行插值的插值内核。权值计算为1/r^p，其中r是到核半径r内邻居点的距离;p(幂参数)是一个正指数(通常p=2)。

如果相邻点p恰好位于要插值的点上，则被插值点取与p相关的值。

vtkVoronoiKernel

描述：vtkVoronoiKernel是一个插值内核，它只返回与要插值的点最近的点。返回值为1.0的单个权重。

vtkIdType vtkVoronoiKernel::ComputeBasis(double x[3], vtkIdList* pIds, vtkIdType)
{
  pIds->SetNumberOfIds(1);
  vtkIdType pId = this->Locator->FindClosestPoint(x);
  pIds->SetId(0, pId);

  return 1;
}


vtkIdType vtkVoronoiKernel::ComputeWeights(double*, vtkIdList*, vtkDoubleArray* weights)
{
  weights->SetNumberOfTuples(1);
  weights->SetValue(0, 1.0);

  return 1;
}

vtkSPHKernel

描述：vtkSPHKernel是D.J. Price描述的光滑粒子流体动力学插值内核的抽象超类。

内核在采样点的半径所定义的空间上运行。核隐含地假设组成输入数据的粒子满足质量守恒等物理性质。因此，这个内核的子类通常不适用于插值过程，因此与vthSPHInterpolator类一起操作。

默认情况下，内核从空间步长^3计算局部粒子体积。

但是，如果同时提供可选的质量和密度数组，则使用它们来计算局部体积。

同样是默认的，插值点周围的局部邻域被计算为CutoffFactor * SpatialStep。(注意CutoffFactor对于每种类型的SPH内核是不同的。)但是，用户可以指定一个CutoffArray，使每个点的截断距离可变。

包含三个子类：vtkSPHCubicKernel、vtkSPHQuarticKernel、vtkSPHQuinticKernel。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/69306.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【css遇到的问题】vue中使用select下拉框，数据绑定但是默认不显示问题

【css遇到的问题】vue中使用select下拉框，数据绑定但是默认不显示问题

文章目录问题描述原因分析问题描述 在vue中使用原生的select下拉框的时候&#xff0c;绑定数据内容但是发现其中默认显示第一条的并不显示 需求实现效果 实际实现效果 循环出select内的数据以后&#xff0c;发现原本默认显示第一条的select框变成了空白&#xff0c;要选择后…
阅读更多...
【Mysql】事务

【Mysql】事务

文章目录一.什么是事务1.1. 事物的属性1.2. 事务的版本支持1.3. 事务的提交方式1.4. 事务常见操作证明事务的回滚事务崩溃情况下验证回滚结论二.事务隔离级别2.1. 如何理解隔离性2.2. 隔离性级别2.3. 脏读,幻读,不可重复读2.4. 查看,设置隔离级别2.5. 隔离性验证三.一致性(Cons…
阅读更多...
T046基于51单片机无线蓝牙控制8位LED灯亮灭proteus仿真原理图PCB

T046基于51单片机无线蓝牙控制8位LED灯亮灭proteus仿真原理图PCB

功能&#xff1a; 0.本项目采用STC89C52作为单片机系统的控制MCU 1.通过蓝牙发送指令控制LED灯 2.通过手机APP可以控制8路LED灯的亮灭&#xff0c;可以全亮全灭。 3.通过手机APP可以控制8路LED灯的亮度。每个灯的亮度有3档。具体控制指令如下 a)发送Ox&#xff0c;开启指定LED灯…
阅读更多...
日常学习之：Yaml 和 Json 有什么区别

日常学习之：Yaml 和 Json 有什么区别

安装 json 是 python 内置 yaml 需要安装 pip install pyyaml格式 对于同样一段数据&#xff1a; test_data {"金山中学":{"101班":{"王宁": {"语文":33,"数学":22,"英语":18}}}}我们用下面的代码分别存入 ya…
阅读更多...
ALE的基本介绍、使用与配置

ALE的基本介绍、使用与配置

本文将介绍ale插件的基本使用与配置&#xff0c;将从linter的介绍到具体插件的使用与bug的修复~ 本文仅仅时抛砖引玉&#xff0c;更多的使用技巧与功能可以查看项目介绍 ALE的基本介绍、使用与配置ale的介绍ale的基本配置与使用查看你可用的linter安装iverilog——for windowal…
阅读更多...
Redisson之lock()和tryLock()的区别

Redisson之lock()和tryLock()的区别

Redisson之lock()和tryLock()的区别和原理解析 在Redisson中 lock() 方法 与 tryLock() 方法是有区别的&#xff01; 我们先来阐述两者的区别&#xff0c;再分析它们的源码。 lock() 与 tryLock() 的区别 &#xff08;1&#xff09;返回值&#xff1a; lock() 是没有返回值…
阅读更多...
Vue中的diff算法深度解析

Vue中的diff算法深度解析

模板tamplate经过parse&#xff0c;optimize&#xff0c;generate等一些列操作之后&#xff0c;把AST转为render function code进而生成虚拟VNode,模板编译阶段基本已经完成了&#xff0c;那么这一章&#xff0c;我们来探讨一下Vue中的一个算法策略–dom diff 首先来介绍下什么…
阅读更多...
Java8 遍历List 使用stream().parallel()并发安全

Java8 遍历List 使用stream().parallel()并发安全

1. parallelStream是什么&#xff1a; java 8引入了并行流的概念来进行并行处理&#xff0c;而并行流(Parallel Stream)利用所有可用CPU内核的优势&#xff0c;并行处理任务。其原理(Parallel Stream)是可以把大任务分成多个小任务执行, 最后再把执行结果进行合并, ForkJoinPoo…
阅读更多...
数仓DWS层之旁路缓存优化

数仓DWS层之旁路缓存优化

优化原因&#xff1a; 外部数据源的查询常常是流式计算的性能瓶颈。以本程序为例&#xff0c;每次查询都要连接 Hbase&#xff0c;数据传输需要做序列化、反序列化&#xff0c;还有网络传输&#xff0c;严重影响时效性。可以通过旁路缓存对查询进行优化。 旁路缓存模式是一种非…
阅读更多...
利用Python海龟绘图画一个世界杯的足球

利用Python海龟绘图画一个世界杯的足球

利用Python海龟绘图画一个世界杯的足球 花有重开日 人无再少年 四年一次的世界杯快要结束&#xff0c;为了纪念此次世界杯&#xff0c;特意用Python画了一个足球。 1.设计思路以及实现效果 世界杯足球实现思路&#xff1a; 首先使用海龟画一个圆形作为足球的外边框。然后在足…
阅读更多...
3天带你走向实战！阿里顶配版Spring全家桶面试进阶笔记有多强？

3天带你走向实战！阿里顶配版Spring全家桶面试进阶笔记有多强？

Spring框架自从诞生以来就一直备受开发者青睐&#xff0c;它涵盖了Spring、Springboot、SpringCloud等诸多解决方案&#xff0c;一般我们都会统称为Spring全家桶&#xff01;出于Spring框架在Java开发者心中中的统治地位&#xff0c;所以不管是面试还是工作&#xff0c;Spring都…
阅读更多...
夜神模拟器+fiddler抓包（抓取APPhttps请求，删除sll证书校验）

夜神模拟器+fiddler抓包（抓取APPhttps请求，删除sll证书校验）

1.安装fiddler https://telerik-fiddler.s3.amazonaws.com/fiddler/FiddlerSetup.exe &#xff08;下载不了直接去官网找&#xff09; 2.配置 开启https请求抓取&#xff0c;不抓https可忽略2.修改或查看端口&#xff08;使用默认8888端口&#xff0c;要自定义端口可修改&#…
阅读更多...
Arduino 定时器中断

Arduino 定时器中断

Arduino 定时器中断 Circuits Arduino 查看原文 简介&#xff1a;Arduino 定时器中断 奥雷里&#xff08;地球、月亮和太阳&#xff09; 立式兰花播种机 胶合板书柜扬声器 计时器中断允许您以非常特定的时间间隔执行任务&#xff0c;而不管代码中发生了什么其他事情。我…
阅读更多...
Unity ILRuntime Debugger使用及常见问题

Unity ILRuntime Debugger使用及常见问题

目录前言1.安装2.使用3.常见问题前言 ILRuntime支持在VS中断点调试&#xff0c;下面说一下ILRuntime Debugger的使用及常见问题。 1.安装 需要下载对应版本的ILRuntime Debugger VS插件。我是在Unity中PackageManager安装的ILRuntime&#xff0c;可以在插件信息中查看版本。…
阅读更多...
记SQL插入emoji成功，但是程序插入失败问题

记SQL插入emoji成功，但是程序插入失败问题

在执行单测时&#xff0c;碰到了以下熟悉的问题 org.springframework.jdbc.UncategorizedSQLException: ### Error updating database. Cause: java.sql.SQLException: Incorrect string value: \xF0\x9F\x92\x8B for column name at row 1 ### The error may involve com.*…
阅读更多...
Java入门教程(16)——条件判断语句

Java入门教程(16)——条件判断语句

文章目录1. if结构1.1 if 单分支结构1.2 if-else 双分支结构1.3 if-else if-else 多分支结构switch 语句switch 多分支结构1. if结构 1.1 if 单分支结构 语法结构: if(布尔表达式){ 语句块 }实例&#xff1a;掷色子游戏 这里给大家扩展一个Math函数 Math.Random()&#xff0c…
阅读更多...
动态规划算法

动态规划算法

1.简介 1.动态规划(Dynamic Programming)算法的核心思想是: 将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法; 2.动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解; 3.与分治法不同…
阅读更多...
项目统一规范包管理器

项目统一规范包管理器

一般来说每个团队都会统一规定项目内只使用一个包管理器&#xff0c;譬如&#xff1a;npm、yarn、pnpm等&#xff0c;我们可以在文档中或者项目根目录REDEM.md中进行描述来形成共识&#xff0c;但毕竟是文档&#xff0c;并不能真正的进行约束&#xff0c;如果有项目成员没有看文…
阅读更多...
SpringBoot自动装配原理分析，看完你也能手写一个starter组件

SpringBoot自动装配原理分析，看完你也能手写一个starter组件

什么是 SpringBoot 2012 年 10 月&#xff0c;一个叫 Mike Youngstrom 的人在 Spring Jira 中创建了一个功能请求&#xff0c;要求在 Spring Framework 中支持无容器 Web 应用程序体系结构&#xff0c;提出了在主容器引导 Spring 容器内配置 Web 容器服务。这件事情对 SpringBo…
阅读更多...
Linux 进程间通信

Linux 进程间通信

目录 进程间通信的必要性 进程间通信的技术背景 进程间通信的本质理解&#xff1a; 管道IPC&#xff1a;匿名管道 示意图 匿名管道的本质原理&#xff1a; demo示例代码&#xff1a; pipe 系统调用 注意&#xff1a; 管道读写的4种情况&#xff1a; 管道的特点&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023