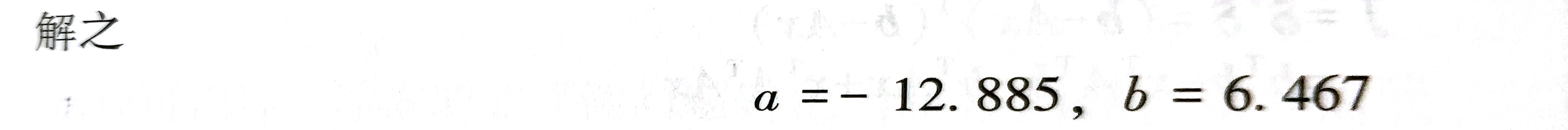数值计算
- 一、误差的来源和分类
- 二、有效数字
- 第一个大题(非线性方程组的迭代法)
- 第二个大题(LU分解)
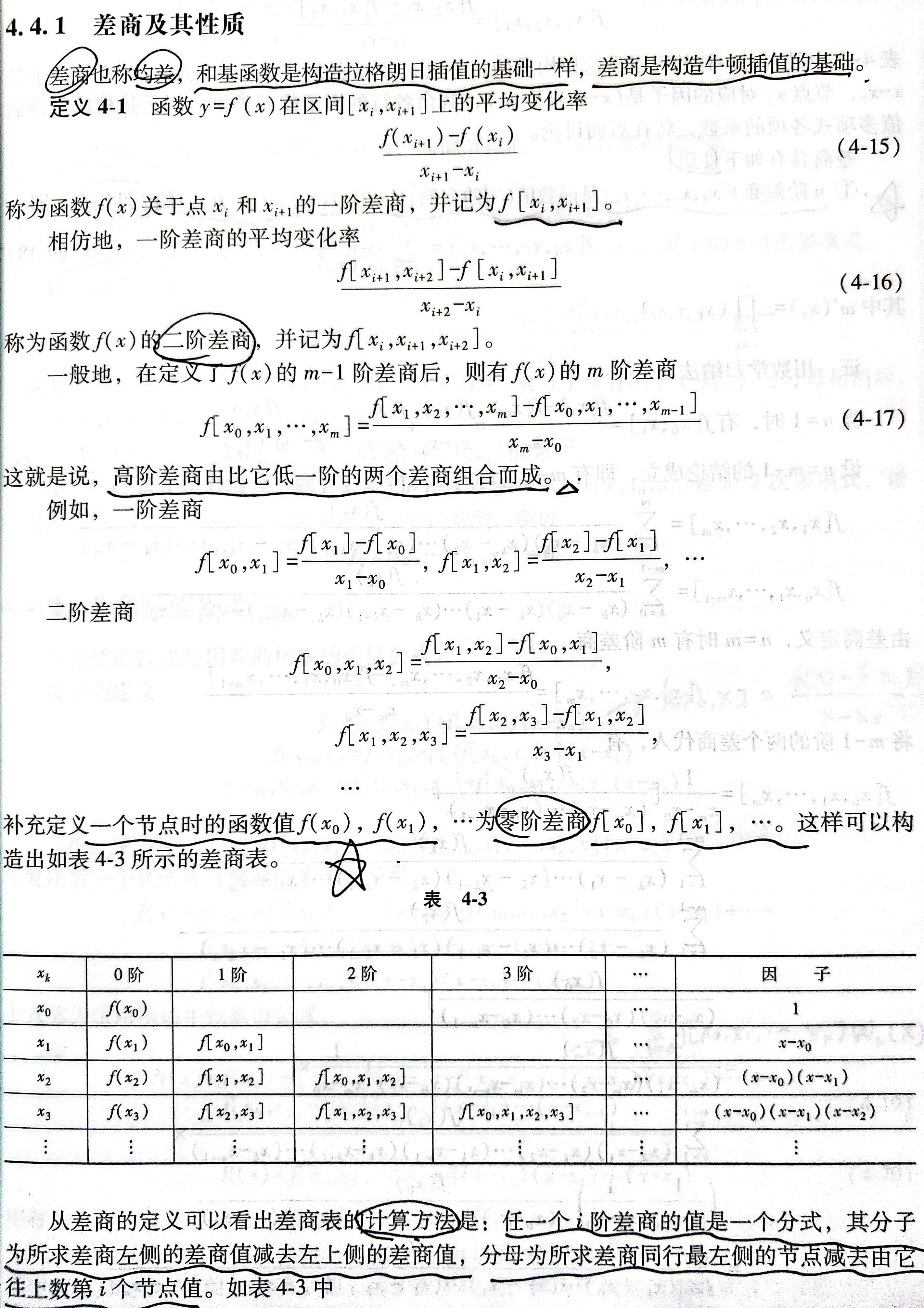
- 第三个大题(牛顿插值法)
- 第四个大题(直线拟合)
一、误差的来源和分类
误差是描述数值计算之中近似值的近似程度
误差按来源可分为:模型误差(描述误差)、观测误差(测量误差)、截断误差、舍入误差(计算误差)
1.模型误差(描述误差):数学模型通常是由实际问题抽象得到的,一般带有误差,这种误差称为模型误差。(这个误差一般来说是不可避免的)
2.观测误差(测量误差):数学模型中的一些参数时通过观测和实验得到的,难免带有误差,这种误差称为观测误差。
注: 以上两种误差并不是数值分析的重点研究内容,因为不可避免。下面说的两种误差是数值分析需要关注和研究的。
3.截断误差: 例如进行taylor展开,
l
n
2
≈
1
−
1
2
+
1
3
−
1
4
+
1
5
ln2 \approx 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}
ln2≈1−21+31−41+51,只取了前5项。这里舍去后面所产生的误差R5被称为截断误差。
4.舍入误差(计算误差):由于计算机只能对有限位数进行运算,在运算中像
e
,
2
,
1
3
e,\sqrt{2},\frac{1}{3}
e,2,31 等都要按舍入原则保留有限位,这时产生的误差称为舍入误差或计算误差。
二、有效数字
设数 x 的近似值
x
∗
=
0.
x
1
x
2
⋯
x
n
⋯
×
1
0
m
−
n
x^* = 0.x_1x_2 \cdots x_n \cdots \times 10^{m - n}
x∗=0.x1x2⋯xn⋯×10m−n,其中
x
i
x_i
xi 为
0
∼
9
0 \sim 9
0∼9 之间的任意数,但
x
1
≠
0
,
i
=
1
,
2
,
3
,
⋯
x_1 \neq 0, i = 1, 2, 3, \cdots
x1=0,i=1,2,3,⋯,
m
m
m 为整数,若
∣
x
−
x
∗
∣
≤
1
2
×
1
0
m
−
n
|x - x^*| \leq \frac{1}{2} \times 10^{m - n}
∣x−x∗∣≤21×10m−n
则称
x
∗
x^*
x∗ 为
x
x
x 的具有
n
n
n 位有效数字的近似值,
x
∗
x^*
x∗ 准确到第
n
n
n 位,
x
1
x
2
⋯
x
n
x_1 x_2 \cdots x_n
x1x2⋯xn 是
x
∗
x^*
x∗ 的有效数字。
这里
x
∗
x^*
x∗ 的位数可以是无限多位,也可以是有限位,如有
n
n
n 位,数值计算中得到的近似数常常是有限位的。
例题: 以
22
7
\frac{22}{7}
722 作为圆周率
π
\pi
π 的近似值,有几位有效数字?
解
∣
π
−
22
7
∣
=
∣
3.
14
592
⋯
−
3.
142
857
⋯
∣
=
0.
001
264
⋯
<
1
2
×
1
0
−
2
\begin{align} \vert \pi - \frac{22}{7} \vert & = \vert 3.\; 14 \; 592 \cdots - 3. \; 142 \; 857 \cdots \vert \\ & = 0. \; 001 \; 264 \cdots < \frac{1}{2} \times 10^{-2} \end{align}
∣π−722∣=∣3.14592⋯−3.142857⋯∣=0.001264⋯<21×10−2
因为
m
−
n
=
−
2
m - n = -2
m−n=−2,题中已知
m
=
1
m = 1
m=1,所以有
n
=
3
n = 3
n=3,即
22
7
\frac{22}{7}
722 作为
π
\pi
π 的近似值有 3 位有效数字。
第一个大题(非线性方程组的迭代法)



第二个大题(LU分解)




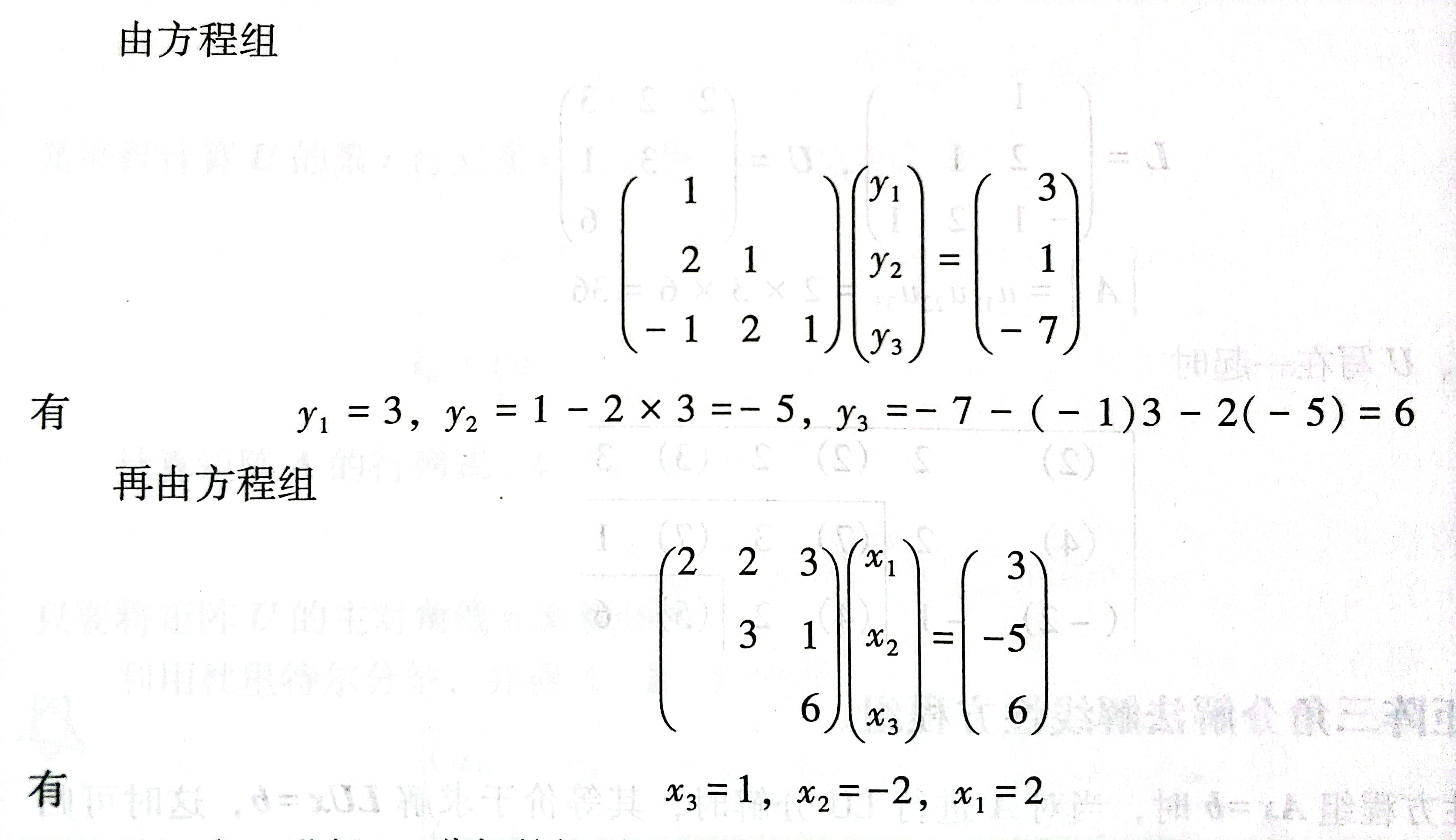



第三个大题(牛顿插值法)



第四个大题(直线拟合)