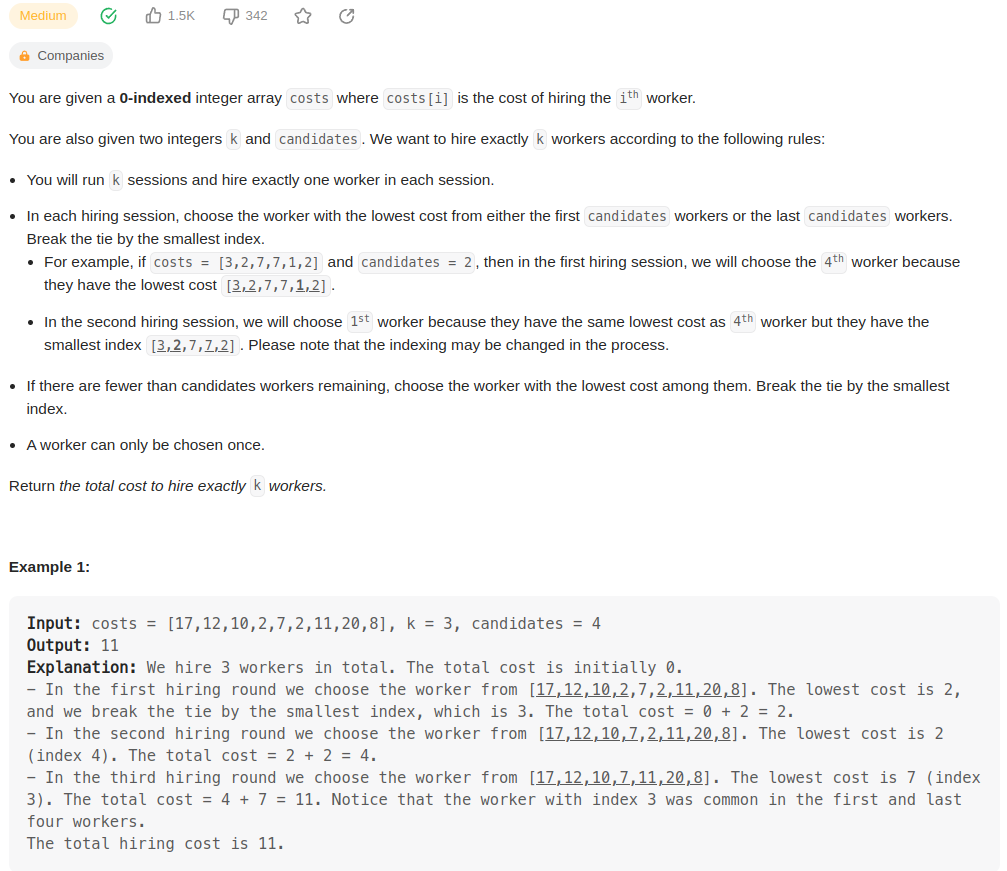
每次从 开头candidates个 和 末尾candidates个 工人中选择一个cost最小的。
如果有2个工人cost相同，就选index较小的。
每个工人的cost在数组costs里。
直到雇够k个工人。
问雇k个工人需要多少cost.

思路：

可以考虑用一个优先队列，按cost排序，如果cost相等就按index排序。
刚开始把 前candidates个 和 后candidates个 (index, cost) 放进优先队列.
假设现在左指针指向candidates（边界处）, 右指针指向n - candidates(边界处，n为costs长度）。
如果选择的index在前candidates个，就把左边再加进一个(index, cost), 同时左边指针右移一步。
同理右边。

如果总共只有k个工人，那是全部要雇的，
2 * candidates > n - k 时，说明在两边的candidates取完k-1个以后，左右边界重叠，也就是说选cost的时候还是在数组全局选的。
这种情况直接把costs排序，按顺序取k个即可。

class Solution {
    public long totalCost(int[] costs, int k, int candidates) {
        int n = costs.length;
        int left = candidates;
        int right = n - candidates;
        long totalCost = 0;

        if (2*candidates > costs.length-k || costs.length==k) {
            Arrays.sort(costs);
            for (int i=0;i<k;i++) {
                totalCost += costs[i];
            }
            return totalCost;
        }

        PriorityQueue<Worker> minHeap = new PriorityQueue<>((a,b)->(a.cost == b.cost?a.idx-b.idx : a.cost-b.cost));

        if(right < left) right = left; 
        for(int i = 0; i < left; i++) minHeap.add(new Worker(i, costs[i]));
        for(int i = right; i < n; i++) minHeap.add(new Worker(i, costs[i]));
        

        while(k > 0) {
            Worker hired = minHeap.poll();           
            totalCost += hired.cost;
            
            if(left < right) {
                if(hired.idx < left) {
                    minHeap.add(new Worker(left, costs[left]));
                    
                    left ++;
                } else {
                    right --;
                    minHeap.add(new Worker(right, costs[right]));
                   
                }
            }       
            k --;
        }       
        return totalCost;
    }
}


class Worker{
    int idx;
    int cost;
    public Worker(int idx, int cost) {
        this.idx = idx;
        this.cost = cost;
    } 
}

其实也可以不考虑index,
左半边和右半边各用一个优先队列，每次从这2个里面找最小cost,
如果是从左边队列里面选的，下次就给左边队列加入元素，右边同理。
用2个指针指向左右边界。

    public long totalCost(int[] costs, int k, int candidates) {
        int n = costs.length;
        int l = 0;
        int r = n - 1;
        long totalCost = 0;

        if (2*candidates > costs.length-k || costs.length==k) {
            Arrays.sort(costs);
            for (int i=0;i<k;i++) {
                totalCost += costs[i];
            }
            return totalCost;
        }

        PriorityQueue<Integer> left = new PriorityQueue<>();
        PriorityQueue<Integer> right = new PriorityQueue<>();

        
        for(int i = 0; i < candidates; i++) {
            left.add(costs[l++]);
            right.add(costs[r--]);
        }
        
        while(k > 0) {
            if(left.peek() <= right.peek()) {
                totalCost += left.poll();
                left.add(costs[l++]);
            } else {
                totalCost += right.poll();
                right.add(costs[r--]);
            }
            k --;
        }       
        return totalCost;
    }