信号与系统复习笔记——采样与通讯系统

采样定理

冲激串采样函数可表示为：

$$p(t)=\sum _{n=-\infty }^{+\infty }\delta (t-nT)$$

周期 $T$ 称为采样周期，而 ${\omega }_s=\frac{1}{T}$ 为采样频率。

对信号 $x(t)$ 进行冲激串采样的结果为：

$$x_p(t)=x(t)p(t)=\sum _{n=-\infty }^{+\infty }x(nT)\delta (t-nT)$$

$x_p(t)$ 本身仍是一个冲激串，幅度为 $x(t)$ 在采样点上的值。

并且有：

$$X_p(j\omega )=\frac{1}{2\pi }[X(j\omega )\ast P(j\omega )]$$

其中：

$$P(j\omega )=\frac{2\pi }{T}\sum _{k=-\infty }^{+\infty }\delta (\omega -k{\omega }_s)$$

已知信号和单位冲激函数做卷积等于该信号的位移：

$$X(j\omega )\ast \delta (\omega -{\omega }_0)=X(j(\omega -{\omega }_0))$$

于是有：

$$X_p(j\omega )=\frac{1}{T}\sum _{k=-\infty }^{+\infty }X(j(\omega -k{\omega }_s))$$

即 $X_p(j\omega )$ 频谱是 $X(j\omega )$ 频谱以周期 $T$ 出现并叠加得到的结果，若频谱无重叠，那么则可以通过低通滤波器得到原信号频谱，这称为 采样定理 ：

设 $x(t)$ 是一个带限信号，在 $|\omega |>{\omega }_M$ 的时候 $X(j\omega )=0$ 。如果 ${\omega }_s>2{\omega }_M$ ，那么 $x(t)$ 就可以被频率为 ${\omega }_s$ 的周期采样串所采样并且唯一的确定。

其中2倍最大频率 $2{\omega }_M$ 称为 奈奎斯特频率 。

零阶保持采样

实际上传输窄和幅度较大的脉冲是相当困难的，我们可以采用零阶保持的方法来进行采样，即在采样的瞬间，直到下一次采样点来临，都是一直保持这一样本值：

这相当于，冲激采样之后，在串联一个零阶保持器：

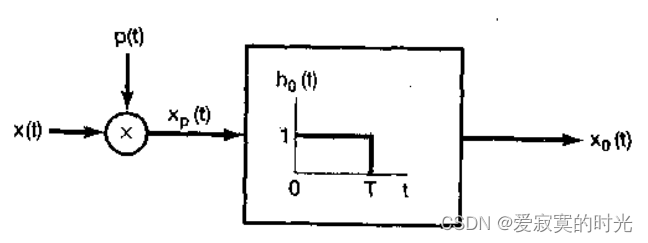
零阶保持器具有一个从0开始的矩形窗口的单位脉冲响应，并且保持时间为采样频率 $T$ 。

利用插值重建信号

插值，就是用一连续信号对一组样本值的拟合。常见的插值方法有：零阶保持插值、线性插值，多项式插值等。

对于冲激串采样的结果 $x_p(t)$ 来说，通入截止频率为 ${\omega }_M$ 的低通滤波器即可还原成源信号，这在时域上相当于做卷积：

$$x_r(t)=x_p(t)\ast h(t)={\int }_{-\infty }^{+\infty }h(t-\tau )\sum _{n=-\infty }^{+\infty }x(nT)\delta (\tau -nT)d\tau =\sum _{n=-\infty }^{+\infty }x(nT){\int }_{-\infty }^{+\infty }h(t-\tau )\delta (\tau -nT)d\tau =\sum _{n=-\infty }^{+\infty }x(nT)h(t-nT)$$

上式体现了低通滤波器的冲激响应曲线的拟合插值过程：

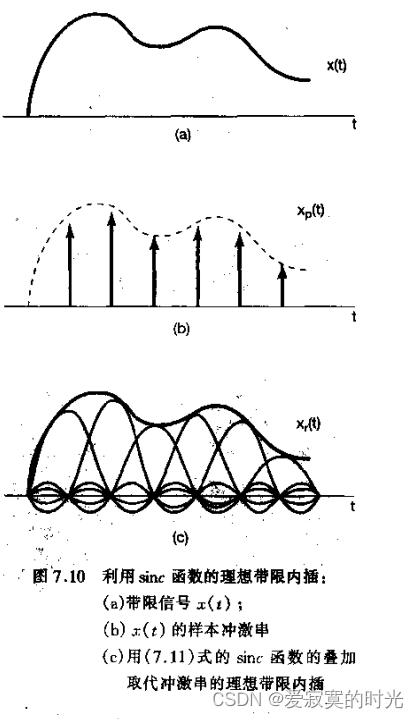
对一个理想的低通滤波器来说，其：

$$h(t)=T\frac{\sin ({\omega }_{c}t)}{\pi t}$$

这种插值方式通常称为 带限插值 。

理想滤波器物理上是不存在的，因此我们通常使用近似的非理想滤波器，会对信号还原造成一定损失，例如零阶保持器，在零阶保持采样中，可以将零阶保持器视为一个低通滤波器，其频率响应和理想滤波器相比如下：

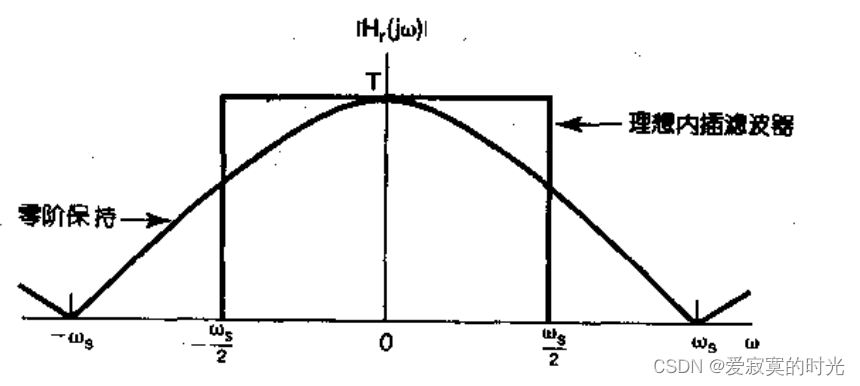
若零阶保持器效果不好，可采用高阶保持器，这里的阶数指，插值后的函数曲线最高在该阶数的导数连续，例如零阶保持器表示在零阶导数都不连续，而线性插值（一阶保持器）表示在零阶导数连续，一阶导数不连续。

易知线性插值的冲激响应是如图的三角波形：

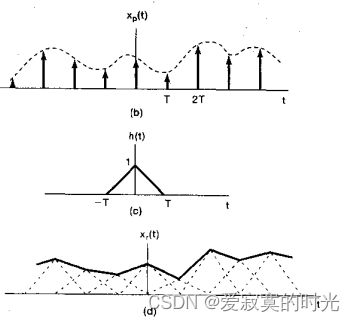
其频率响应和理想滤波器相比如下：

其频率响应为：

$$H(j\omega )=\frac{1}{T}[\frac{\sin (\omega T/2)}{\omega /2}{]}^2$$

欠采样

当 ${\omega }_s>2{\omega }_M$ 的时候，采样信号的频谱是由原信号频谱重复组成，当 ${\omega }_s>2{\omega }_M$ 的时候，采样信号的频谱不再是重复原信号频谱，而是发生 混叠现象 ，因此利用低通滤波器也不能把信号还原出来。

显然，对于采样点上的信号值通常能够准确的还原出来，即：

$$x_r(nT)=x(nT)$$

我们使用 $x(t)=\cos {\omega }_{0}t$ 来说明欠采样的效果，当采用不同的采样频率的时候：

$$\begin{array}{cc}{x}_r(t)=\cos {\omega }_{0}t=x(t)& {\omega }_0=\frac{{\omega }_s}{6}\\ x_r(t)=\cos {\omega }_{0}t=x(t)& {\omega }_0=\frac{2{\omega }_s}{6}\\ x_r(t)=\cos [({\omega }_s-{\omega }_0)t]\ne x(t)& {\omega }_0=\frac{4{\omega }_s}{6}\\ x_r(t)=\cos [({\omega }_s-{\omega }_0)t]\ne x(t)& {\omega }_0=\frac{5{\omega }_s}{6}\end{array}$$

当混叠发生的时候，原始频率 ${\omega }_0$ 就被混叠成一个较低的频率 ${\omega }_s-{\omega }_0$ 。当 ${\omega }_0={\omega }_s$ 的时候，被重建的信号就是一个常数。

对于带相位的 $x(t)=\cos ({\omega }_{0}t+\varphi )$ 来说，傅里叶变换的形状是相同的，只不过在 ${\omega }_0$ 的位置的冲激有个幅度因子 $\pi e^{j\varphi }$ 在 $-{\omega }_0$ 的时候冲激有个幅度因子 $\pi e^{-j\varphi }$ ，当发生混叠的时候，此时：

$$x_r(t)=\cos [({\omega }_s-{\omega }_0)t-\varphi ]$$

这个在相位上有个颠倒，称为 相位倒置 。

最后需要注意一点是，采样定理一定是采样频率大于信号最大频率的2倍，等于是不够的，考虑：

$$x(t)=\cos (\frac{{\omega }_s}{2}t+\varphi )$$

若通过频率 ${\omega }_s$ 采样，得到的输出为：

$$x_r(t)=\cos \varphi \cos (\frac{{\omega }_s}{2}t)$$

可见只有当 $2\pi$ 倍相位偏移的时候，才能正确还原。

连续时间信号的离散时间处理